带有缺失数据的广义半参数模型的均值借补估计

内容提要：本文在响应变量随机缺失时，给出了广义半参数模型中响应变量的2个均值拟似然借补估计。证明了它们具有渐近正态性，给出了估计的渐近偏差与渐近方差，并进行模拟比较。
    关键词：广义半参数模型 缺失数据 局部线性估计 拟似然措补估计 渐近正态性
    作者简介：李志强北京化工大学理学院，北京100029；北京工业大学应用数理学院，北京100022；薛留根北京工业大学应用数理学院，北京100022
    一、引言和估计方法在响应变量随机缺失时，Cheng[1]应用核回归估计借补缺失值的方法给出θ=EY的借补估计。Wang，Linton和Hdardle[2]给出了半参数回归模型的均值函数的多个核回归借补估计。Chen，Fan，Li和Zhou[3]考虑了非参数广义回归模型中响应变量的均值的拟似然借补估计方法。本文在响应变量随机缺失时，给出了广义半参数模型的拟似然估计方法，再利用完全数据方法及由选取概率给出的倾向得分加权估计方法，得到响应变量均值的拟似然借补估计。我们讨论了估计渐近正态性，并进行模拟比较。
    假定Y关于(X，Z)的条件期望函数为μ(x，z)=E[Y｜X=x，Z=z]，这里x∈R，z∈R^d。又假设对给定的已知联系函数g（·），满足
    
    
    
    表1和表2分别给出模拟容量为50，100，200的样本，在上述窗宽和缺失概率下，利用本文方法重复做500次得到的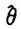的模拟结果。由表中取值情况可知，两种估计方法精度相差不大，但当样本容量较小时加权借补估计相对要好些。