通货膨胀的惯性特征与波动性（上）——基于HNKPC模型

内容提要：通货膨胀是宏观经济中最重要的问题之一，对此进行研究具有重要意义。结合中国通货膨胀的惯性特征，对Gali和Gertler(1999)的新凯恩斯混合菲利普斯曲线模型加以扩展，构建了通货膨胀的ARCH模型，并运用中国1991年1月到2011年6月的宏观月度数据进行经验检验。结果表明，中国通货膨胀具有显著的惯性特征，存在波动聚集现象；产出缺口对当期通货膨胀的影响最为显著，其次是滞后一期通胀。

关键词：通货膨胀，通胀惯性，ARCH模型，波动性

        作者简介：尹双明(1976-)，男，山东济南人，山东财经大学经济学院讲师，中国人民大学经济学2009级博士研究生。主要研究方向：宏观经济学及其流派。

一、引言

通货膨胀是宏观经济研究中最重要的问题之一，产出、就业、消费等诸多宏观经济问题的研究都与通货膨胀紧密相关，同时控制通货膨胀也是宏观经济政策的重要目标之一，研究通货膨胀的意义无须赘述。

中国自改革开放以来，经历了数次通货膨胀，通货膨胀问题受到广泛关注。尤其是自上世纪90年代初期开始，中国经济步入转轨阶段，开始向社会主义市场经济转变，经济结构中市场方面的因素逐渐增多，对这个期间通货膨胀进行研究也更为重要。

菲利普斯曲线是研究通货膨胀问题的核心工具。Phillips(1958)发现了失业率和货币工资率两者在统计上存在稳定的负相关关系。Samuelson和Solow(1960)说明了失业率和通货膨胀率之间的交替关系。Friedman(1968a)、Phelps(1967，1968)和Lucs(1972，1973)分别将适应性预期和理性预期引入菲利普斯曲线。现在对通货膨胀的研究主要是以新凯恩斯菲利普斯曲线(NKPC)模型为基础。早期的NKPC模型是以Taylor(1979，1980)^[1]、Rotemberg(1982)^[2]和Calvo(1983)^[3]的模型为代表，即TRC模型。在此基础上，Moore和Fuhrer(1995)^[4]、Gali和Gertler(1999)^[5]提出新凯恩斯混合菲利普斯曲线模型。Mankiw和Ries(2002)提出粘性信息菲利普斯曲线模型。与传统菲利普斯曲线相比，NKPC引入垄断竞争、粘性价格、理性预期和粘性信息，从而具有坚实的微观基础。

在实证检验方面，国外学者已经进行了充分的经验检验。国内的研究主要是以NKPC为理论基础对菲利普斯曲线模型进行经验检验。大多数研究者使用Hansen(1982)^[6]提出的GMM方法来估计模型参数，从实证研究的结果看，既形成许多一致的观点，也存在许多相互对立的观点，尚未在整体上达成一致。

本文以Gali和Gertler(1999)的混合模型为理论基础，重点关注通货膨胀的惯性特征，对该模型进行拓展并建立ARCH模型，利用1992年1月到2011年6月的月度宏观数据进行实证检验，拟从波动性这一崭新视角揭示中国通货膨胀的规律性特征。文章第二部分是国内文献回顾；第三部分是理论模型；第四部分经验检验；第五部分是结论。

二、国内文献回顾

国内学者以NKPC模型为理论基础，建立计量模型，结合宏观经济数据进行了大量的经验检验。

李振、杨晓光(2007)^[7]、张成思(2008)、赖小琼和黄智淋(2011)使用的计量模型包括通胀滞后一期π_t-1、通胀预期E_tπ_t+1和产出缺口y_t三个变量；陈彦斌(2008)^[8]在Gordon(1996)的三角模型、Galíand Gertler(1999)混合模型的基础上，提出了包括π_t-1、E_tπ_t+1、需求拉动和成本推动的四因素NKPC模型；耿强、张永杰和朱牡丹(2009)^[9]构建的计量模型涉及的变量主要有π_t-1、E_tπ_t+1、y_t和有效汇率q；顾标和王剑锋(2010)^[10]、杨小军(2011)^[11]的计量模型包括π_t-1、E_tπ_t+1和mc_t(边际成本对其稳态值偏离的百分比)三个变量，杨小军将mc_t分解为贷款利率和劳动报酬份额；曾利飞、徐剑刚和唐国兴(2006)^[12]也使用了π_t-1、E_tπ_t+1和mc_t三个变量，并把mc_t分解为劳动力边际成本、资本边际成本和进口中间品边际成本。

由此可知，通货膨胀所涉及的解释变量包括π_t-1、E_tπ_t+1、y_t、mc_t、利率和汇率等，其中π_t-1、E_tπ_t+1、y_t或mc_t^①是最主要的变量，这一点可以从经验检验中参数的估计值看出，如赖小琼和黄智淋(2011)对π_t-1、E_tπ_t+1和y_t三个变量的参数估计值分别是0.3915、0.5067和0.1042；耿强、张永杰和朱牡丹(2009)的估计值分别是0.30、0.73和0.22；李振、杨晓光(2007)对π_t-1、E_tπ_t+1的参数估计值分别是0.42和0.58；杨小军(2011)对这两个变量的参数估计给出了变化范围：0.46-0.49和0.47-0.74。

由于NKPC模型中含有E_tπ_t+1项，在对计量模型进行估计时，研究者较多地使用Hansen(1982)提出的GMM估计方法。如曾利飞、徐剑刚和唐国兴(2006)、张成思(2008)、顾标和王剑锋(2010)、杨小军(2011)、赖小琼和黄智淋(2011)等。此外，李振、杨晓光(2007)采用了VAR估计方法，而陈彦斌(2008)采用了最小二乘估计方法。在参数估计过程中，大量检验使用的是季度数据，少数检验使用了年度数据。

已有的实证检验很少从波动性视角对通货膨胀进行研究。基于此，本文重点关注通货膨胀的惯性特征，并以此为依据对理论模型进行拓展并建立波动性计量检验模型。

三、理论模型

假设垄断竞争厂商在每一个时期调整价格的概率为1-θ，维持价格不变的概率为θ，厂商调整价格的时机是随机的，且独立于自上次调整后经历的时间。厂商按其定价行为不同分为两类：比例为1-ω的前向型厂商，在给定的时间约束下，利用所有可用的信息，通过最小化其损失函数来确定价格；比例为ω的后向型厂商则利用简单的拇指规则来定价。

经济中第t期的价格总水平为t-1期价格水平和t期新设定价格的加权平均和，即：

p_t=θP_t-1+(1-θ)p_t^* (1)

p_t^*为t期新设定的价格。以p_t^f表示前向型厂商t期设定的价格，以p_t^b表示后向型厂商t期设定的价格，则有：

p_t^*=(1-ω)p_t^f+ωp_t^b (2)

根据Calvo(1983)模型，由前向型厂商的最优定价行为，可得：

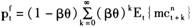(3)

后向型厂商遵循拇指定价规则，可知：

p_t^b=p_t-1^*+π_t-1 (4)

由(1)到(4)式，可以推导出混合菲利普斯曲线：

π_t=λmc_t+γ_fE_t{π_t+1}+γ_bπ_t-1 (5)

λ=(1-ω)(1-θ)(1-βθ)φ^-1，γf=βθφ^-1，γ_b=ωφ^-1，φ=θ+ω[1-θ(1-β)]，θ表示价格粘性的程度，ω表示后向定价的程度，β为贴现因子。这就是Gali和Gertler(1999)的混合模型。

由实际边际成本与产出缺口存在近似线性关系：

mc_t=ky_t (6)

将(6)代入(5)式，可得：

π_t=λky_t+γ_fE_t{π_t+1}+γ_bπ_t-1 (7)

(7)式就是GG混合模型的表达式。

采用适用性预期规则对通货膨胀进行预期，即根据以前若干期的实际通货膨胀来预期。这样，预期通货膨胀E_t{π_t+1}由滞后1到k₁期的通货膨胀来决定，即

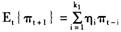(8)

强调通胀惯性的作用，π_t受到从滞后1到k₂期通胀水平的影响。从t-k₂到t-2的影响可以表示为：

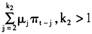(9)

将(8)、(9)代入(7)式，可得：

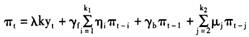(10)

为简化问题，再假定有k₁=k₂=p，则由(10)式可以推导出：

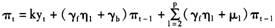(11)

进一步简化为：

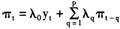(12)

其中，λ₀=λk，λ₁=γ_fη₁+γ_b，当2≤q，l≤p时，λ_q=γ_fη₁+μ₁。

这样，当期通货膨胀率由当期产出缺口和从滞后1到p期的通货膨胀率来表示。

四、经验检验

(一)计量检验模型

根据(12)式，可以建立如下计量检验模型：

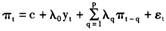(13)

其中c为常数项，ε为随机扰动项

(二)数据说明

本文选取1991年1月到2011年6月期间的月度数据为样本。中国经济结构由计划经济向社会主义市场经济的变革始于上世纪九十年代初期，此前，经济结构整体上具有明显的计划经济特征，1991年至今的这段期间，经济结构上具有明显的市场经济特征，更符合模型的假设环境。

在对菲利普斯曲线模型进行实证检验时，往往使用季度数据。本文以波动性为视角，旨在通过研究通货膨胀的波动特征来揭示通货膨胀的规律，需要使用高频数据，所以选择月度数据而没有选择季度数据。

模型中涉及的变量有通货膨胀率和产出缺口：(1)通货膨胀率采用居民消费价格指数(CPI)环比，该数据来自国家统计局网站数据库。(2)产出缺口用实际产出偏离潜在产出的百分比来表示，即y_t=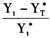，Y_t为t期的实际产出，Y_t^*为t期的潜在产出，实际产出=名义GDP/GDP平减指数。名义GDP和GDP平减指数数据来自国家统计局网站数据库，名义GDP和GDP平减指数只提供季度数据，由此可以计算得到实际产出的季度数据，再利用计量软件将季度数据转化为月度数据。然后，采用H-P滤波方法(λ取14400)进行趋势分解，将实际产出分解为趋势部分T_t和周期部分C_t，即Y_t=T_t+C_t，趋势部分即潜在产出，产出缺口由C_t/T_t给出。

(三)数据的描述性统计

表1 通货膨胀率的统计特征

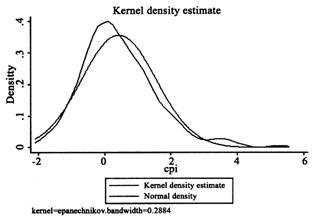
图1 通货膨胀率核密度与正态密度

通货膨胀样本数据均值为0.434，标准差为1.121，方差为1.256。偏度衡量观测值分布偏离均值的状况。偏度的绝对值越小，表明该数据的正态对称性越好。样本数据的偏度为0.878，偏度大于0，说明数据呈右偏分布状态。峰度衡量序列分布的凸起状况。峰度值越大，说明该数据的正态峰越明显，样本数据峰度为4.516，大于3，说明其凸起程度大于正态分布的凸起程度，呈尖峰状态。图1也直观显示，变量通货膨胀率的分布与正态分布有一定差距。

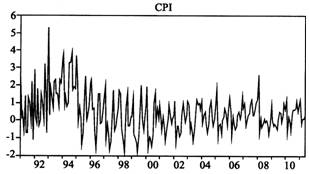
图2 通货膨胀率的时间趋势

从时间趋势图来看，通货膨胀率总体趋势从1991-1994年迅速走高，且波动幅度较大；从1994-2000年缓慢走低，波动幅度很大；从2000年之后，总体趋势基本呈水平状态，围绕零线上下波动，波动幅度较小。

(四)检验结果分析

由于本文使用的是时间序列的数据，为了避免数据不稳定而导致参数估计出现偏差和伪回归，应该先对数据进行平稳性检验。检验结果见表2。

表2 时间序列稳定性检验

对变量π和y分别进行DF、ADF、PP、DF-GLS检验，结果显示π在5%的显著水平下拒绝原假设，即不存在单位根。而y不能通过稳定性检验，为非稳定序列。进一步对y的一阶差分进行单位根检验，仍然不能通过稳定性检验。再进一步对y的二阶差分进行单位根检验，其ADF、PP、DF-GLS检验统计量分别为-8.881、50.211和16.823，通过1%的显著水平的平稳性检验。y的二阶差分为平稳过程，是二阶单整，即I(2)。

（未完待续）

责任编辑：夏雨