人口结构转变、家庭教育投资与中国经济增长（二）

    
    命题5：在其他参数保持不变的情况下，人口年龄结构变化(老年人口相对青壮年人口增多)、家庭赡养支出比例a对经济增长的影响是不确定的。
    证明：将(15)、(18)、(20)、(21)式计算整理后可得到：
    
    
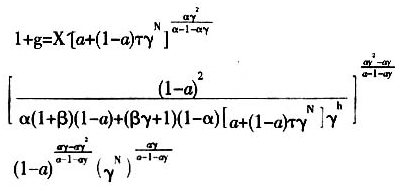
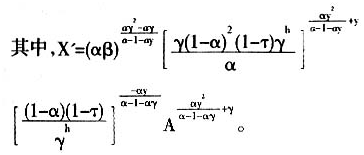
    从证明结果③可知，在其他参数保持不变的情况下，只需满足α＜1/(1＋γ)，人口年龄结构的变化(老年人口相对青壮年人口增多)将促进经济增长，反之将阻碍经济增长。而家庭赡养支出比例对经济增长的影响作用较为复杂，这主要是因为家庭赡养支出比例在增加教育投资(命题1)的同时却降低了人均储蓄率以及人均物质资本存量(命题2、命题3)。因此，经济增长速度取决于家庭赡养支出比例对教育投资与人均储蓄率以及人均物质资本存量的影响程度的比较，家庭赡养支出比例在理论上并不必然影响经济增长速度。
    三、实际数值模拟
    为了能够预测人口年龄结构变化以及家庭养老给中国家庭储蓄率、教育投资和经济增长带来的影响，本文拟对理论模型中所使用的各参数进行调整，以印证其合理性。为了避免参数设置的随意性，本文拟参照已有研究对相关参数的取值。大多相关研究都估计每一年的主观贴现率为0.99，因此假设每期时间跨度为30年，那么模型的主观贴现因子β应为0.74[20]。对于我国的资本产出弹性，张(Zhang)等估算的物质资本产出弹性α为0.4[14]，刘永平等估算的家庭教育投资对于子代人力资本的产出弹性γ约为0.267[19]。在其他宏观经济参数的设定上，本文使用了1978－2007年中国经济的相关数据进行估算。经计算，1978－2007年中国人口年均增长率约为1.1％，因此模型中的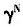＝1.39。另有一些学者就我国改革开放以来的全要素增长率(TFPG)进行了估算，得出其基本处于1.2％－3.9％，为了便于研究，本文假定为2％。1997年以后，国家为了做实个人账户，将个人账户占工资的比例调整为8％，所以本文认为τ＝8％。对于a值，可以通过实际的中国老年人口负担比和养老金替代率进行估算，估算后，中国实际家庭赡养支出比例约为20％左右。关于相对应的A和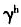的取值，根据1978－2007年中国经济的相关数据和前文理论模型中的相关公式，通过逆推和数据拟合可确定A＝9.09、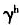＝1.08。
    (一)人口年龄结构变化、家庭赡养支出比例与人均储蓄率
    图2给出了物质资本产出弹性α为0.5、0.4和0.3时人口年龄结构与人均储蓄率关系的数值模拟。可以看出，随着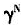的减小，人均储蓄率s上升，当α＝0.4时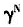，由1.5降低到0.5，人均储蓄率由25.30％上升到27.05％。还可看出，如果所有条件不变，物质资本产出弹性α越大，人均储蓄率s越高。这一点同现实相符合。一般来说，经济越发达的国家物质资本的产出弹性越大，经济相对不发达的国家物质资本的产出弹性较小，两者相比，经济相对不发达的国家储蓄率偏高。
    
    图2人口年龄结构与家庭人均储蓄率关系的数值模拟(α变，其他参数不变)
    图3给出了物质资本产出弹性α为0.5、0.4和0.3时家庭赡养支出比例与家庭人均储蓄率关系的数值模拟。可以看出，随着α的增大，人均储蓄率s下降，当α＝0.4时，a由0.0变化为1.0，人均储蓄率由37.84％下降到0。还可看出，同图2相似，如果所有条件不变，随着物质资本的产出弹性α增大，人均储蓄率s增加。
    
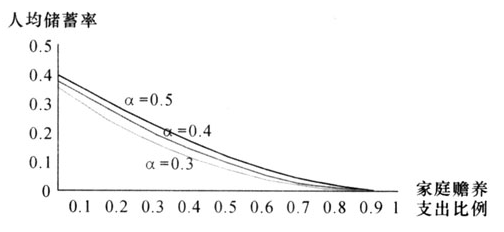
    图3家庭赡养支出比例与家庭人均储蓄率关系的数值模拟(α变，其他参数不变)
    (二)人口年龄结构、家庭赡养支出比例与家庭教育投资率
    图4给出了物质资本产出弹性α为0.5、0.4和0.3时人口年龄结构与家庭教育投资率关系的数值模拟。可以看出，随着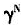的减小，教育投资率r_e下降，当α＝0.4时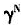，由1.5减少到0.5，教育投资率r_e由3.72％下降到3.04％。还可看出，如果所有条件不变，物质资本的产出弹性α越大，教育投资率越低。这是因为物质资本的产出弹性越大，理性行为人势必将其大部分收入用于物质资本积累，最终影响教育投资率的增长。
    
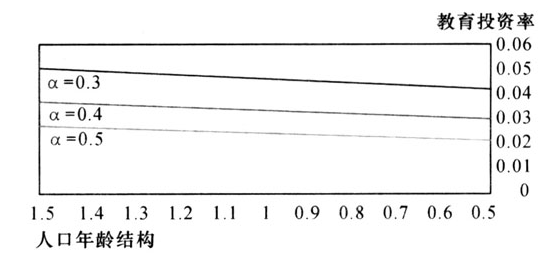
    图4人口年龄结构变化与家庭教育投资率关系的数值模拟(α变，其他参数不变)
    图5给出了物质资本产出弹性α为0.5、0.4和0.3时家庭赡养支出比例与家庭教育投资率关系的数值模拟。可以看出，随着a的增大，教育投资率r_e先上升再下降，呈倒U型变化，即家庭赡养支出比例a先促进教育投资率r_e增长，但当家庭赡养支出比例a达到一定的界限后，将阻碍教育投资率r_e增长。当α＝0.4时，a由0.0变化为1.0，教育投资率r_e先由1.82％上升到4.60％，随后开始下降，最终降到0。还可看出，如果所有条件不变，物质资本的产出弹性α越大，教育投资率r_e越低，家庭赡养支出比例对教育投资率影响的拐点出现得也越晚，同时教育投资率对家庭赡养支出比例的变化越不敏感。
    
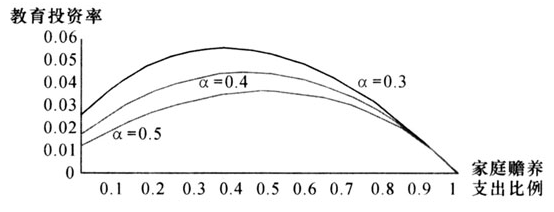
    图5家庭赡养支出比例与家庭教育投资率关系的数值模拟(α变，其他参数不变)
    (三)人口年龄结构、家庭赡养支出比例与经济增长
    图6给出了人口年龄结构与经济增长关系的数值模拟。(a)是物质资本产出弹性α为0.5、0.4和0.3时人口年龄结构与经济增长关系的数值模拟，可以看出，随着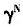的减小，经济增长率g上升，当α＝0.4时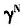，由1.5减少到0.5，经济增长率g由－1.33％上升到18.64％。还可看出，如果所有条件不变，物质资本的产出弹性α越大，经济增长率g下降幅度越快。(b)是家庭教育投资对于子代人力资本产出弹性γ为0.4、0.3和0.2时人口年龄结构与经济增长关系的数值模拟，可以看出，随着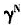的减小，经济增长率g上升，当γ＝0.3时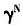，由1.5减少到0.5，经济增长率g由0.07％上升到22.78％。还可看出，如果所有条件不变，家庭教育投资对于子代人力资本的产出弹性γ越大，经济增长率g越高。(c)是人力资本增长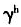为1.15、1.1和1.05时人口年龄结构与经济增长关系的数值模拟，可以看出，随着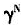的减小，经济增长率g上升，当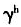＝1.1和1.05时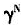，由1.5减少到0.5，经济增长率g分别由－1.15％、－1.45％上升到18.84％、18.51％。还可看出，如果所有条件不变，人力资本增长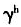越大，经济增长率g越高。(d)是社会保障税率τ为0.15、0.1和0.05时人口年龄结构与经济增长关系的数值模拟，可以看出，随着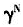的减小，经济增长率g上升，当τ＝0.1和0.05时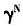，由1.5减少到0.5，经济增长率g分别由－2.49％、0.51％上升到17.65％、20.12％。还可看出，如果所有条件不变，社会保障税率τ越低，经济增长率g越高。
    
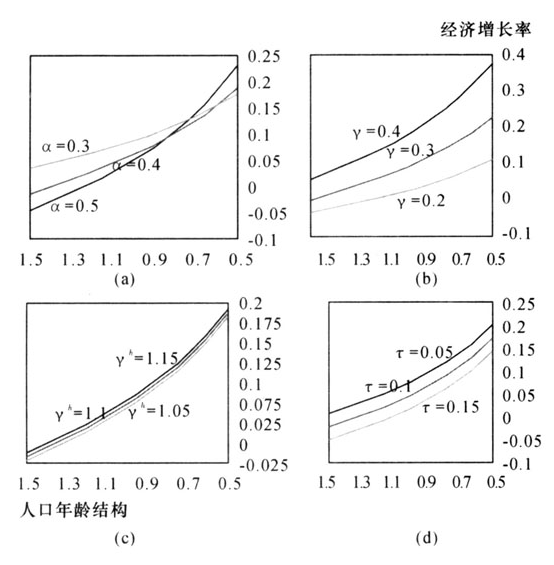
    图6人口年龄结构与经济增长关系的数值模拟
    图7给出了家庭赡养支出比例与经济增长关系的数值模拟。(e)是物质资本产出弹性α为0.5、0.4和0.3时人口年龄结构与经济增长关系的数值模拟，可以看出，随着a的增大，经济增长率g下降，当α＝0.4时，a由0.05变化为0.95④，经济增长率g由3.93％下降到－30.23％。还可看出，如果所有条件不变，物质资本的产出弹性α越小，经济增长率g越高。(f)是家庭教育投资对于子代人力资本产出弹性γ为0.4、0.3和0.2时人口年龄结构与经济增长关系的数值模拟，可以看出，随着a的增大，经济增长率g下降，当γ＝0.3时，a由0.05变化为0.95，经济增长率g由6.25％下降到－31.25％。还可看出，如果所有条件不变，家庭教育投资对于子代人力资本的产出弹性γ越大，经济增长率g下降幅度越快。(g)是人力资本增长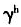为1.15、1.1和1.05时人口年龄结构与经济增长关系的数值模拟，可以看出，随着a的增大，经济增长率g下降，当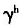＝1.1和1.05时，a由0.05变化为0.95，经济增长率g分别由4.09％、3.83％下降到－29.95％、－30.41％。还可看出，如果所有条件不变，人力资本增长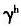越大，经济增长率g越高。(h)是社会保障税率τ为0.15、0.1和0.05时人口年龄结构与经济增长关系的数值模拟，可以看出，随着a的增大，经济增长率g下降，当τ＝0.1和0.05时，a由0.05变化为0.95，经济增长率g分别由2.38％、6.55％下降到－30.65％、－29.61％。还可看出，如果所有条件不变，社会保障税率τ越低，经济增长率g越高。
    
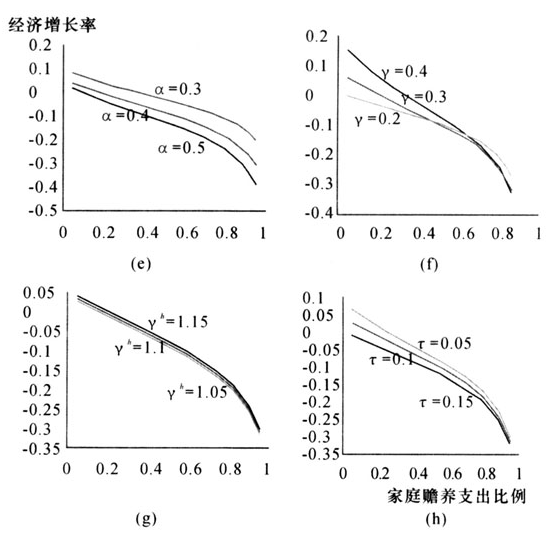
    图7家庭赡养支出比例与经济增长关系的数值模拟
    四、结论与政策含义
    本文从一个两期的世代交叠模型入手，分析了在家庭和社会两种养老模式共同作用下人口结构转变对家庭教育投资与经济增长的影响，并在此基础上通过数据模拟验证了其影响。本文的主要结论如下：(1)随着人口年龄结构的变化(老年人口相对青壮年人口增多)，人均储蓄率上升；随着家庭赡养支出比例的增加，人均储蓄率下降。(2)随着人口年龄结构的变化(老年人口相对青壮年人口增多)，教育投资率(教育投资占可支配收入的比重)下降。在满足α(1－α)(1＋β)(1－τ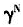)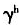＞(βγ＋1)的情况下，家庭赡养支出比例增加将促进教育投资率增长，反之将抑制其增长。(3)只需满足α＜1/(1＋γ)，人口年龄结构的变化(老年人口相对青壮年人口增多)将促进经济增长，反之将阻碍经济增长。而家庭赡养支出比例在增加教育投资的同时却降低了人均储蓄率以及人均物质资本存量，因此经济增长速度取决于家庭赡养支出比例对教育投资与人均储蓄率以及人均物质资本存量的影响程度的比较，家庭赡养支出比例在理论上并不必然影响经济增长速度。利用我国实际参数进行的数值模拟结果表明，在当前条件下，随着人口年龄结构的变化，经济增长率上升，而家庭赡养支出比例增加抑制经济增长。
    本文研究结论的基本政策含义在于：(1)要大力提升劳动者素质。劳动者素质的提升可以弥补人口结构转变带来的劳动力数量短缺，而劳动者素质提升的关键是教育。因此，各级政府应把教育摆在优先发展的战略地位，保证财政资金优先保障教育投入、公共资源优先满足教育和人力资源开发需要，努力实现更高水平的普及教育，形成惠及全民的公平教育，特别是要大力发展职业教育，提高普通劳动者与就业需求间的匹配性，有效增强其就业稳定性。(2)要扩大社会保障覆盖面，提高社会保障支出水平。社会保障的缺失必然会增大家庭保障支出比例，从而挤占家庭消费以及对子女教育、健康等方面的支出，最终对经济的快速发展产生消极影响。对农村地区而言，影响效果可能更大，社会保障缺失会削弱农村家庭对人力资本的投资，使农村人力资源相对过剩与人力资本短缺矛盾凸显，最终抑制农民收入增长以及农村发展。因此，应扩大社会保障覆盖面，逐步建立城乡一体的社会保障体系。另外我国中央财政的社会保障支出严重不足，据统计，公共财政支出中社会保障支出比例不足15％，在世界各国中处于较低水平。因此，还应进一步调整财政支出结构，增加社会保障投入，逐步提高社会保障支出占财政支出的比重，为更好地应对人口老龄化冲击提供资金保证。
    需要指出的是，本文的研究还存在一些不足。首先，在模型设定时假定行为人从青壮期到老年期死亡率为零，也未包括老年人因突然死亡而留给子代的非意愿馈赠财富；其次，为了研究的方便，仅以现收现付制作为中国养老保障的唯一模式，但随着人口老龄化的日趋加剧，现收现付制将会出现支付危机，而且中国也已由单一的现收现付模式过渡到现收现付与个人账户并存的混合养老保障模式。在本文的世代交叠模型中，尚未考虑这些问题，这样可能会使模拟结果与实际存在一定的误差。
    注释：
    ①本文所使用的数据均来自1996－2010年的《中国统计年鉴》，其中家庭教育投资率利用家庭教育文化娱乐服务支出占家庭总支出的比例来衡量。
    ②很容易验证积累制和人口年龄结构变化没有关系，只和投资绩效有关系。该假定不会对分析结果产生影响。
    ③限于篇幅，此处略去证明过程，感兴趣者可直接向笔者索要。
    ④由于在稳态经济增长率的求解方程中分母含有1－a，因此在家庭赡养支出比例与经济增长关系的数值模拟中，a的取值范围均为0.05－0.95。
    参考文献：
    [1]BLOOM D E, WILLIAMSON J G. Demographic Transitions and Economic Miracles in Emerging Asia[J].The World Bank Economic Review, 1998, 12: 419-455.
    [2]FAIR, DOMINGUEZ. Effects of the Changing US Age Distribution on Macroeconomic Equations[J].American Economic Review, 1991, 81: 1276-1294.
    [3]LINDH. Medium-term Forecasts of Potential GDP and Inflation Using Age Structure Information[R].Sweden: Uppsala University, 1999.
    [4]BATINI N, JUSTINIANO A, LEVINE P. Robust Inflation-forecast-based Rules to Shield against Indeterminacy[J].Journal of Economic Dynamics and Control, 2006, 30: 1491-1526.
    [5]BLANCHARD O J. Debt, Deficits, and Finite Horizons[J].The Journal of Political Economy, 1985, 93: 223-247.
    [6]BECKER G, KEVIN M, TAMURA T. Human Capital, Fertility, and Economic Growth[J].Journal of Political Economy, 1990, 98: 12-37.
    [7]EHRLICH I, LU F T. Intergenerational Trade, Longevity, and Economic Growth[J].Journal of Political Economy, 1991, 99: 1029-1059.
    [8]FOUGERE M, MERETTE M. Population Ageing and Economic Growth in Seven OECD Countries[J].Economic Modeling, 1999, 16: 411-427.
    [9]CARNEIRO, HECKMAN. Inequality in America: What Role for Human Capital Policy?[M].MIT Press, 2003: 77-240.
    [10]SEBNEM K O. A Stochastic Model of Mortality, Fertility, and Human Capital Investment[J].Journal of Development Economics, 2003, 70: 103-118.
    [11]SADAHIRO A, SHIMASAWA M. The Computable Overlapping Generations Model with an Endogenous Growth Mechanism[J].Economic Modeling, 2002, 20: 1-24.
    [12]BLACKBURN, CIPRIANI. A Model of Longevity, Fertility and Growth[J].Journal of Economic Dynamics and Control, 2002, 26: 187-204.
    [13]ANDERSON B. Scandinavian Evidence on Growth and Age Structure[J].Region Studies, 2001, 26: 377-390.
    [14]ZHANG JIE, JUNSEN ZHANG, LEE R. Rising Longevity, Education, Savings, and Growth[J].Journal of Development Economics, 2003, 70: 83-101.
    [15]GRADSTEIN, KAGANOVICH. Ageing population and education finance[J].Journal of Public Economics, 2004, 88: 2469-2485.
    [16]王德文，蔡昉，张学辉．人口转变的储蓄效应和增长效应[J].人口研究，2004(5): 2－11.
    [17]郭剑雄．人力资本、生育率与城乡收入差距的收敛[J].中国社会科学，2005(3): 27－40.
    [18]郭震威，齐险峰．“四二一”家庭微观仿真模型在生育政策研究中的应用[J].人口研究，2008(2): 5－15.
    [19]刘永平，陆铭．从家庭养老角度看老龄化的中国经济能否持续增长[J].世界经济，2008(1): 65－77.
    [20]邵宜航，刘雅南，张琦．存在收入差异的社会保障制度选择——基于一个内生增长世代交替模型[J].经济学季刊，2010(4): 1559－1574.^