2.关于货币的供给函数
任何一种商品的供给都是来自于它的生产者。而在现代银行体系下,货币的直接供给者是商业银行,而商业银行的背后是中央银行。所以,弗里德曼与施瓦兹[27]在其合作的经典著作《美国货币史(1867—1960)》一书中给出了后来成为标准教科书中重要内容的货币供给公式:

即:M1=H×k或者M1=(Cu+R)×k (2)
又因为,狭义货币供给量(M1)被定义为:通货(Cu)+贷款总额(D),即,M1=Cu+D。所以,货币创造乘数就表示为:
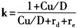 (3)
(3)
其中,Cu/D表示现金存款比;rd表示法定准备率;re表示超额准备率。
在货币的供给机制中,基础货币(又称高能货币H)被认为是由中央银行完全控制的,而“货币创造乘数”则较为复杂。根据公式(3),法定准备率(rd)是由中央银行完全控制的,外生的。而超额准备率(re)是由银行与借贷者共同决定的。影响它的因素很多,其中就包括“贷款利率”。如果假设其他因素保持不变,那么当贷款利率提高时,商业银行会有增加贷款的动力,从而降低它的超额准备率(re)。而r。的下降,会导致货币创造乘数的提高,从而增加货币供给量。因此,如果我国的货币供给是内生的(且供给曲线向右上方倾向),即,货币供给量受利率的影响,那么其中的机理就在于此。当然,是否内生还需要在后文中加以证实,因为虽然这种机制在理论上存在,但在现实中这种作用机制是否明显还需要定量的分析。
根据上述论证,本文认为“货币的供给函数”可构造为如下的一般形式:
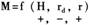
其中,M表示货币供给量;H表示基础货币,它与M之间应该呈正相关关系;rd表示法定准备率,它与M之间应该呈负相关关系;r表示贷款利率,如果货币供给是内生的,那么它与M之间应该呈正相关关系。
3.货币供求函数的计量模型
综合以上分析,本文所构造的货币的供求函数方程组的一般形式可表示如下三个模型。
模型一:
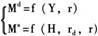 (5)
(5)
模型二:
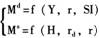 (5)′
(5)′
模型三:
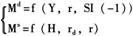 (5)″
(5)″
对于实际的计量分析,需要给出具体的函数形式,本文将具体的形式设定为:
模型一:
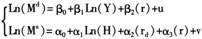 (6)
(6)
模型二:
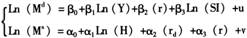 (6)′
(6)′
模型三:
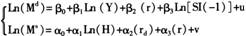 (6)″
(6)″
之所以设定为半对数函数形式,原因是:首先,需求函数是遵循了大多数学者进行同类研究时所采取的形式;其次,供给函数之所以被设定为线性形式,其机理是:通过对(2)式的左右两边同时取对数得到:Ln(Ms)=Ln(H)+Ln(k)。之后,进一步假设Ln(k)与rd、r,以及常数之间,呈近似的线性关系,从而可得(6)式、(6)′式以及(6)″式中的半对数线性形式。此外,采用上述形式还有一个好处:每个解释变量前的系数都有明确的经济含义。
四、计量分析
本文将以联立方程组(6)—(6)″式为基础,使用2004—2009年的季度数据进行回归分析。
1.数据处理
第一,对于“名义收入(Y)”,由于是季度数据,所以该序列呈现明显的季节波动,该波动将严重影响回归的质量,因此在进行回归分析之前,需要进行季节性调整。本人使用X11对原序列进行调整,之后再进行对数处理。
第二,对于“利率r”,本文使用“一年期贷款名义利率”。由于该变量没有现成的季度数据,所以本文先构造该变量的月度数据,然后再构造成季度数据。在构造月度数据的过程中,采用加权平均的方法,比如,2006年8月份,前19天利率为5.85,从第20天开始变为6.12,那么该月的平均利率=5.85×19/31+6.12×(1-19/31)≈5.95。从月度数据向季度数据转换时,使用Eviews的自动转换功能(加权平均)。
第三,法定准备率(rd)也需要进行手工处理,方法及过程“利率”的处理方法相同。
第四,股票指数。本文选用上证指数在每个季度的最大值。
第五,货币数量使用M1。
数据总结如表1所示。
表1 2004—2009年季度数据
|
时间 |
GDP(亿元) |
X11处理后的GDP |
一年期贷款利率(%) |
基础货币(H)(亿元) |
法定准备金率(%) |
上证指数(最高值) |
M1(亿元) |
|
2004Q1 |
33 420.60 |
85 318.54 |
5.31 |
50 461.59 |
7.00 |
1 845.80 |
231 654.60 |
|
2004Q2 |
70 405.90 |
89 731.87 |
5.31 |
51 305.77 |
7.36 |
1 870.01 |
238 427.50 |
|
2004Q3 |
109 967.60 |
94 151.85 |
5.31 |
53 150.02 |
7.50 |
1 570.04 |
243 757.00 |
|
2004Q4 |
159 878.30 |
96 567.46 |
5.50 |
58 856.11 |
7.50 |
1 507.98 |
253 207.70 |
|
2005Q1 |
39 117.00 |
99 833.29 |
5.58 |
57 588.32 |
7.50 |
1 394.58 |
264 588.90 |
|
2005Q2 |
81 913.00 |
104 415.90 |
5.58 |
57 360.22 |
7.50 |
1 315.76 |
275 785.50 |
|
2005Q3 |
126 657.00 |
108 441.80 |
5.58 |
60 771.21 |
7.50 |
1 285.68 |
287 438.30 |
|
2005Q4 |
184 937.00 |
111 691.00 |
5.58 |
64 343.13 |
7.50 |
1 233.62 |
298 755.50 |
|
2006Q1 |
45 316.00 |
115 621.10 |
5.58 |
62 551.31 |
7.50 |
13 76.85 |
310 490.70 |
|
2006Q2 |
95 429.00 |
121 708.30 |
5.77 |
63 096.19 |
7.50 |
1 781.64 |
322 756.40 |
|
2006Q3 |
147 341.00 |
126 209.20 |
5.98 |
66 187.10 |
8.23 |
1 848.43 |
331 865.40 |
|
2006Q4 |
216 314.00 |
130 551.20 |
6.12 |
77 757.83 |
8.75 |
2 839.92 |
345 577.90 |
|
2007Q1 |
54 756.00 |
139 755.00 |
6.16 |
76 990.09 |
9.60 |
3 441.19 |
364 104.70 |
|
2007Q2 |
115 999.00 |
148 048.60 |
6.47 |
82 663.98 |
10.80 |
4 545.60 |
377 832.20 |
|
2007Q3 |
180 101.00 |
154 316.80 |
6.90 |
88 212.33 |
11.78 |
5 836.24 |
393 098.90 |
|
2007Q4 |
265 810.00 |
160 320.00 |
7.31 |
101 545.40 |
13.12 |
6 429.68 |
403 401.30 |
|
2008Q1 |
66 284.00 |
169 228.90 |
7.47 |
104 224.20 |
14.94 |
5 796.72 |
423 054.50 |
|
2008Q2 |
140 478.00 |
179 435.50 |
7.47 |
115 353.10 |
16.34 |
3 972.95 |
443 141.00 |
|
2008Q3 |
217 026.00 |
186 050.20 |
7.43 |
117 336.10 |
17.50 |
3 096.66 |
452 898.70 |
|
2008Q4 |
314 045.00 |
189 257.00 |
6.23 |
129 222.30 |
16.83 |
2 381.34 |
475 166.60 |
|
2009Q1 |
69 754.80 |
178 179.00 |
5.31 |
124 276.70 |
15.50 |
2 522.74 |
530 626.70 |
|
2009Q2 |
148 080.70 |
189 252.60 |
5.31 |
123 929.70 |
15.50 |
3 146.61 |
568 916.20 |
|
2009Q3 |
231 139.40 |
198 139.80 |
5.31 |
133 406.60 |
15.50 |
3 651.20 |
585 405.30 |
|
2009Q4 |
340 506.90 |
205 135.00 |
5.31 |
143 985.00 |
15.50 |
3 525.59 |
610 224.50 |
数据来源:国家统计局网站、中国人民银行网站。
2.各变量的平稳性检验
在进行回归之前,需要对所有变量进行平稳性检验。本文使用Eviews 6.0中的ADF单位根检验法得到的结果如下:变量Ln(M1)、Ln(H)、Ln(SI)、rd,以及r均为I(2)过程。经过X11处理后的名义GDP的对数值Ln(Y)是一个I(1)过程。由此可见,被解释变量Ln(M1)是I(2)过程,解释变量中最高也是I(2)过程,因此在它们之间有可能呈现“协整关系”(这里只给出结果,如需检验过程,请与作者联系)。
3.应用两阶段最小二乘法(TSLS)估计供求函数的各项参数
需求函数和供给函数的估计结果如表2、表3所示。
表2 被解释变量:Ln(M1)
|
解释变量 |
模型一 |
模型二 |
模型三 |
|
C |
-0.59(-1.31) |
0.25(0.75) |
0.49(1.07) |
|
Ln(Y) |
1.10(25.03) |
0.95(26.40) |
0.92(17.19) |
|
r |
-0.10(-4.71) |
-0.12(-6.69) |
-0.14(-5.02) |
|
Ln(SI) |
|
0.13(4.49) |
|
|
Ln(SI(-1)) |
|
|
0.16(3.31) |
|
R2 |
0.97 |
0.99 |
0.98 |
|
|
0.97 |
0.99 |
0.98 |
|
DW |
0.84 |
1.39 |
1.67 |
注:括号内的为t值。
表3 被解释变量:Ln(M1)
|
解释变量 |
模型一 |
模型二 |
模型三 |
|
C |
-2.31(-1.71) |
-2.15(-1.80) |
-2.11(-1.74) |
|
Ln(H) |
1.27(10.32) |
1.26(11.29) |
1.26(11.15) |
|
Rd |
-0.05(-3.90) |
-0.05(-4.31) |
-0.05(-4.26) |
|
R |
0.03(1.27) |
0.03(1.45) |
0.02(1.15) |
|
R2 |
0.97 |
0.98 |
0.98 |
|
|
0.97 |
0.97 |
0.97 |
|
DW |
1.23 |
1.32 |
1.50 |
注:括号内的为t值。
4.模型残差的平稳性检验
经检验,三个模型的需求函数及供给函数的残差都是平稳的,因此可以说三个模型都不太可能出现“伪回归”的问题。当然三个模型拒绝“伪回归”的可能性是不一样的,相对而言,模型三以更大概率拒绝。同时考虑其他的显著性指标后,笔者认为模型三最可靠。因此,如果要估计我国货币的需求函数,可以考虑使用模型三中需求函数的形式(这里只给出结果,如需检验过程,请与作者联系)。
5.计量结果
首先,三个模型的拟合度都很高,主要变量都通过了显著性检验(常数项除外),各项系数的正负号也与理论预计的相一致,而且残差经检验都是平稳的,所以可以认为这些模型的建立是成功的。
其次,计量结果显示,在考察期内,三种模型都显示出:货币供给函数中利率系数的估计量都没有通过显著性检验。因此,无法拒绝“利率前的系数是零”的结论。换言之,在(r,LnM1)的坐标系中,货币供给曲线最有可能的形态是垂直的。因此,本文得出结论:在现阶段我国的货币供给依然可视为外生变量。
6.对可能的批评提供的补充说明
(1)三个模型中的货币供给曲线的常数项都没有通过显著性检验,因此如果去除掉结果会怎样?笔者对三种情况都进行了尝试。结果是利率同样不显著。
(2)如果表示机会成本的变量中引入“通货膨胀”变量,结果会怎样?本人对三种情况都进行了尝试。结果是:通货膨胀变量本身都不显著,而且利率依然不显著。原因是,上述研究使用都是名义量,价格变化的因素已经包含其中了。
(3)如果使用其他利率变量,结果会怎样?笔者使用一年期存款利率,结果是一样的,而且显著程度均有所下降。
(4)货币的供给曲线会不会是非线性的?有可能,但笔者没有进行研究。
由于篇幅所限,上述计量的过程省略。
五、总结
根据本文计量分析的结果,目前我国的货币供给依然是一个外生变量。其中的原因很复杂,但直接原因显然只能是:商业银行的货币供给行为对利率不敏感。因为如果货币供给是内生的,即供给曲线是一条向右上方倾斜的曲线,那么就意味着,当利率上升时,商业银行会多提供贷款。而现实中,一方面贷款利率的提高不一定意味着“利差”的扩大;另一方面,贷款利率的上升在提高了收益的同时也加大了贷款的风险。因此,两方面原因导致商业银行的货币供给行为对利率并不敏感。此外,在我国,存贷款利率还不能完全反应出市场的供求,这也是我国货币供给外生性的另一个重要原因。
货币供给的外生性意味着,在短期内我国的央行依然可以通过相机抉择的货币政策干预社会的经济生活。但与此同时,一些关于“货币外生供给”似是而非的论断也需要做出澄清:
1.货币供给具有外生性并不意味着货币政策的中间变量应该选择货币数量
一个变量是否适于作为央行的中间目标与该变量是否为内生变量没有关系。在许多国家中,作为中间目标的“利率”本身就是一个内生变量。虽然有越来越多的国家把利率(而不是货币数量)作为中间变量,但主要原因是货币数量的信息不容易获得,决策者在得到该信息时会有较长的时滞与信息失真,因此控制起来难度很大;相反,对利率信息的获悉则非常便捷,因此调控起来相对容易得多。所以,本文在论证了我国货币供给依然是外生变量之后,并不认为应该将货币数量作为中间目标。
2.货币供给具有外生性并不意味着一国的央行在货币供给上可以“为所欲为”
央行在决定货币供给量时一定有自己的目标,如通货膨胀率目标、经济增长目标、汇率目标等等。因此,绝不可能在货币供给上“为所欲为”。但这样一来是否出现矛盾?因为通常许多人认为“货币供给外生论”等同于认为央行可以任意移动垂直的供给曲线。这里需要澄清的是:判断一个变量的外生与否,取决于我们考察的系统范围。经济学将判断货币供给外生与否的定义确定为货币供给量是否与“利率”相关,即明确了考察的系统边界是“利率一货币供给量”。而如果我们扩大了这个边界,比如考虑整个经济系统,那么货币供给量当然就是内生的,因为央行的决策一定会受到其他变量的影响。这就是为什么许多学者利用格兰杰因果检验的方法验证了我国的货币供给是内生的,因为他们检验出的实际上是在更大的系统中,类似经济增长、通货膨胀等经济变量内生引起了货币供给量。
基金项目:北京交通大学基本科研业务费项目“收入差距的变化对经济增长影响的计算机模拟分析”(2011JBM237)
注释:
①因为如果货币供给是内生的,即货币供给曲线是倾斜的,那么用单方程估计就会产生系统性的偏差。
参考文献:
[1]奥利维尔·布兰查德.宏观经济学[M].刘新智等译,北京:清华大学出版社,2010.
[2]鲁迪格·多恩布什,斯坦利·费希尔,理查德·斯塔兹.宏观经济学[M].王志伟译,北京:中国人民大学出版社,2010.
[3]胡宗伟.外生与内生货币供给理论评述[J].上海金融学院学报,2006,(1).
[4]Basil, J. M. The Endogenous Money Supply [J].Journal of Post Keynesian Economics, 1988,10(3):372 -385.
[5]Thomas,
[6]史永东.我国货币供给内生性和外生性的实证研究[J].统计研究,1998,(1).
[7]魏巍贤.中国货币供给的超外生性检验[J].系统工程理论与实践,2000,10).
[8]Engle, R. F., Hendry,D. F., Richard,J. F. Exogeneity [J].Econometrica,1983,51(2):277-304.
[9]易纲.中国的货币供求与通货膨胀[J].经济研究,1995,(5).
[10]刘斌,黄先开,潘虹宇.货币政策与宏观经济定量研究[M].北京:科学出版社,2001.
[11]吴卫华.中国货币需求函数的协整分析[J].上海财经大学学报,2002,(1).
[12]汪红驹.用误差修正模型估计中国货币需求函数[J].世界经济,2002,(5).
[13]易行健.中国的长期均衡与短期动态货币需求模型估计(1978—2002)[C].2003年经济学年会论文.
[14]王莉.中国货币需求函数的误差修正模型估计:1995-2004[J].上海金融,2005,(10).
[15]蒋瑛琨,赵振全,刘艳武.中国货币需求函数的实证分析——基于两阶段(1978-1993、1994-2004)的动态检验[J].中国软科学,2005,(2).
[16]王晓芳,王学伟.中国股票市场对货币需求的影响[J].财经科学,2008,(3).
[17]巴曙松.转轨经济中的货币乘数波动与货币控制[J].国际金融研究,1998,(1).
[18]孙伯银.货币供给内生的逻辑[M].北京:中国金融出版社,2003.7.
[19]崔建军.货币供给的性质:内生抑或外生[J].经济学家,2005,(3).
[20]王国松.货币供给的制度内生与需求内生实证研究[J].财经研究,2008,(6).
[21]李晓华,侯传波,陈学彬.我国货币内生性问题的实证研究[J].上海财经大学学报,2003,(10).
[22]宁咏.内生货币供给:理论假说与经验事实[M].北京:经济科学出版社,2002.
[23]黄武俊,陈漓高.外汇资产、基础货币供应与货币内生性——基于央行资产负债表的分析[J].财经研究,2010,(1).
[24]李少斌,刘朝阳.我国货币需求函数结构比较研究[J].上海金融,2007,(9).
[25]何运信.货币需求函数中到底要不要引入制度变量[J].中国物价,2006,(3).
[26]张笑冰.中国股市市值对货币需求影响的实证分析[J].经济师,2007,(1).
[27]米尔顿·弗里德曼,安娜·J.施瓦茨.美国货币史(1867-1960)[M].巴曙松等译,北京:北京大学出版社,2009.
责任编辑:夏雨

 2
2