贝叶斯视角下时变参数VAR建模（上）——兼论“斜率之谜”

内容提要：中国渐进式的改革实践要求中国宏观时间序列的建模能够允许参数平滑变化，而传统的VAR模型对此无能为力。本文详细阐述了在贝叶斯估计框架下，如何利用MCMC算法，建立时变参数VAR模型的过程，并利用该模型对徐高（2008）的数据重新进行了拟合，发现其文中提出的“斜率之谜”现象不复存在，因此时变参数VAR模型在拟合中国宏观时间序列方面更为精准。
    关键词：贝叶斯 时变参数 VAR “斜率之谜”
    作者简介：孙焱林，陈普，华中科技大学经济学院；熊义明，上海交通大学安泰经济管理学院。
    引言
    自Sims（1980）提出向量自回归（VAR）模型以来，该技术得到了广泛的应用和发展。特别地，联系着短期约束、长期约束，以及新近发展的符号约束（Sign Restrictions）、异方差约束（Heteroskedasticity Restrictions）的结构向量自回归（SVAR）模型在宏观时间序列分析中发挥着越来越重要的作用，而且包含在该模型内的脉冲响应和方差分解也往往能够给出十分直观的经济含义。
    尽管如此，该项建模技术仍然存在着极大的局限性。其中最令人感到缺乏真实性的是，该模型假定估计的系数是不变的，这就意味着，无论在该样本期内是否发生了经济结构的某种平滑变化，该模型对此无能为力。如果不能捕捉这种变化，那么得到的结果很可能失真。
    实际上，自1978年来，中国渐进式的改革实践必然会对宏观经济数据带来某种平滑变化。毫无疑问，传统的VAR或者SVAR模型无法捕捉这种变化，那么由传统的VAR或者SVAR模型得出的结论在某种程度很可能偏离了经济实际。事实上，国内已经有部分文献在讨论一些令人诧异的经济现象。徐高（2008）提出了“斜率之谜”的概念，即在Blanchard和Quah（1989）的长期约束下，通胀率对供给冲击和需求冲击的脉冲响应的方向和经典IS-LM宏观经济理论出现了矛盾，从而使得总需求曲线斜率为正，总供给曲线斜率为负。无独有偶，高士成（2010）也发现了类似的现象。我们不排除该现象的出现可能会有其他原因，但是如果能够有机会拟合一些估计系数随机变化的VAR模型，然后再来检查“斜率之谜”，如果该现象消失了，那么经济系统的平滑变化应该得到相当程度的确认，则传统的VAR模型在此处应该存在着模型误设。
    幸运的是，Cogley和Sargent（2001）、Cogley和Sargent（2005）、Primiceri（2005）在建立系数随机变化的VAR模型方面做出了巨大的贡献。考虑到允许系数随机变化时，待估系数将成倍增加，他们无一例外地均选择了带有一定先验约束的贝叶斯估计框架，在该框架下，他们建立的模型很好的捕捉了一些传统模型无法捕捉的经济现象。特别地，在该模型下，徐高（2008）提到的“斜率之谜”现象也消失了。
    考虑到中国渐进式的改革实践，该类模型对于中国的宏观经济时间序列拟合应是十分贴切的。不过，由于该模型在设定和估计上均存在一定的复杂性，国内理论以及实证文献鲜有触及。本文力图清晰阐述该模型的建立过程，为提高国内实证研究水平略尽绵薄之力。
    一、模型的构建
    系数随时间变化（Time Varying Parameters）的VAR模型有两类，一类是假定VAR误差项的方差—协方差不随时间变化，简称TVP-VAR；一类假定误差项的方差—协方差也是时变的（Stochastic Volatility），简称TVP-VAR-SV。本节先从TVP-VAR开始，然后再扩展至TVP-VAR-SV。
    1.TVP-LVAR模型
    （1）TVP-VAR模型的设定。TVP-VAR模型是一个系数随时间变化的VAR模型，通过系数的变化来捕捉系统的结构变化。一般地，一个诱导型VAR可以书写如下：
    
    因为本文使用的是贝叶斯估计框架，按照通常的做法，我们对式（1）的数据堆积形式进行一些变换，以便陈述在该框架下的估计方法。易知对每一个观测数据，有：
    
    
    其中，服从独立同分布N（0，Q）。式（2）一般称为度量方程，可以看到除了误差项的分布有些许异样外，其具备经典多元回归方程的标准形式，式（3）称为状态方程，它们就是TVP-VAR的基本模型设定——一个系数随时间变化的VAR模型。
    在继续往下阐述之前，此处先给出一个在贝叶斯估计理论中的经典结论，它会在后面的建模过程中多次使用。
    
    式（4）和式（5）的结论在文后会多次使用。
    （2）TVP-VAR模型的估计。式（2）和式（3）需要估计的参数包括时变的，的方差—协方差矩阵∑和的方差—协方差矩阵Q一共三个参数块。类似这样的模型，一般均通过卡尔曼滤波利用极大似然估计得到，但应该可以理解，在这样一个非线性高维空间取极值是一件非常困难的事情。这也是选择贝叶斯估计的原因之一。
    贝叶斯估计的关键是要求能够得到参数块（如，∑和Q）的后验联合分布，在过去，这样的联合分布求取同样十分困难，但自从MCMC（Markov Chain Monte Carlo）算法②在贝叶斯估计中的广泛使用以来，这样的联合分布求取不再令人望而生畏。因为通过MCMC算法，可以把一些高维的问题分解成一个个低维的问题来解决。或者说，其可以将一个联合分布的估计问题利用MCMC算法的Gibbs抽样或者Metropolis-Hastings抽样将其转化成一个一个的条件分布来解决，一般而言，这些条件分布往往十分容易得到。
    
    接下来，分别阐述先验分布如何设定，后验分布如何求取。
    第一，先验分布的设定。对于其先验分布，可以借鉴Primiceri（2005），而不使用平凡先验③。首先从样本中选取一部分譬如τ个观测值，作普通的最小二乘估计，从而可以得到最初状态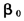的一些先验信息，从而得到先验分布：
    
    
    
    看到式（6）这种分解，可以理解这又是一个将高维分解为低维的抽样过程，根据前述对式（2）和式（3）的线性假设，易知式（6）右边的项均服从正态分布，关键是求得这些正态分布的均值和方差，我们便可以进行抽样了。
    接下来，我们来求取式（6）右边各项中各正态分布的均值和方差。
    
    再来看式（6）右边其他所有连乘项，它们均是利用后一期的信息来校正前一期的估计（即该类文献中所常称的后向递归），上述标准的卡尔曼滤子公式不再适用了。但是可以换一种思考方式，这种校正模式体现在状态方程式（3）中，可以将向量看作是在第t期时逐步增加M（1+Mp）个观测值的过程，这样的话，式（3）本身又看作了一个度量方程，于是比照标准卡尔曼滤子更新方程式（7）和式（8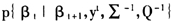），的均值和方差可以写为：
    
    至此，则可以获得所有待估参数的后验条件分布，然后就可以使用Gibbs抽样来得到联合分布，得到所有参数的估计值。
    （3）TVP-VAR模型的识别。通过上述步骤，可以得到诱导VAR在各个时期的系数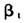，及方差协方差阵∑和Q。此时可以通过对式（1）中的系数矩阵右乘一个识别矩阵C，来获得结构VAR系数矩阵，再将其变换为向量移动平均形式，从而获得脉冲响应。本文后续的实证分析中，就是通过长期约束来获得C，从而获得结构VAR系数。
    2.TVP-VAR-SV模型
    如果放弃式（2）中∑的时常假设，转而考虑∑的时变性，模型将更为艰深，但其脉络依然清晰。我们仍然可以从最简单的情况譬如单变量的随机波动开始，然后再将其扩展至多变量即VAR的情形。
    （1）单变量的随机波动。Jacquier等（1994）为单变量随机波动提供了经典的建模方法，Kim等（1998）为使算法更为有效，做出了改进。一般地，在他们的文献中均假设：
    
    实际上，在TVP-VAR-SV模型的假设中，都假定φ=1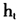，是一个随机游走，这样实际上大大简化了上述模型，我们有
    
    
    

（未完待续）