rt*选取的是美国10年期国债收益率,其他变量的含义与数据来源如表2所示。所有变量均经过移动平均进行季节调整,财政支出数据经过名义GDP剔除规模效应。此外,为避免资产价格与消费物价指数的共线性过于强烈,我们选择中国房地产价格指数(house)作为资产价格(h)的代理变量,且认为名义汇率具有静态预期的形式(Etet+1=et),简记变量ret=rt*+Etet+1=rt*+et。关于样本期间选择,由于中国人民银行资产负债表在2002年之前并未披露国外负债项目,另外,从2011年开始储备货币口径进行了较大调整,因此,本文选取2002年1月至2010年12月间的月度数据加以分析,各变量月度数据均经过移动平均方法进行季节调整。各变量均为跨期变化量,即一阶差分后的数据,经过ADF单位根检验均显著拒绝原假设,即验证为平稳过程,直接进行回归分析的结果是可靠的,不存在伪回归的问题。
表2 变量选取与数据来源
|
实证变量 |
含义 |
表达式 |
数据来源 |
|
mm |
广义货币乘数,广义货币供给量(M2)与基础货币(MB)之比 |
|
PBC |
|
Δmm |
广义货币乘数的变化量 |
Δmmt=mmt-mmt-1 |
PBC |
|
Δp |
CPI表征的通货膨胀率 |
Δpt=ln(CPIt)-ln(CPIt-1) |
WIND |
|
Δreer |
实际有效汇率(REER)变化率 |
Δreert=ln(reert)-ln(reert-1) |
BIS |
|
re |
美国10年期国债收益率(r*)与间接标价法下人民币对美元名义汇率(e)之和 |
Ret=rt+et |
FRS |
|
Δre |
re的变化量 |
Δret=ret-ret-1 |
FRS |
|
gap |
实际产出(y)缺口,实际潜在产出y*由HP滤波方法给出 |
|
WIND |
|
Δg |
政府支出(G)占名义产出(GDP)之比的变化量 |
|
Bloomberg |
|
Δhouse |
房地产景气指数(house)的变化量 |
Δhouset=houset-houset-1 |
WIND |
(二)中国货币冲销操作的描述性分析
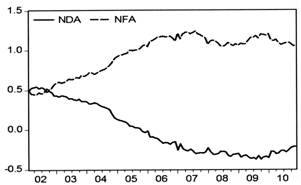
图2 国内信贷(NDA)与外汇占款(NFA)
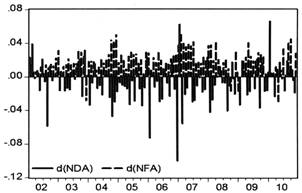
图3 国内信贷增量与外汇占款增量
图2和图3分别显示了国内信贷(NDA)与外汇占款(NFA)、国内信贷增量(ΔNDA)与外汇占款增量(ΔNFA)的变化关系,从中可以看出近年来中国货币当局持有国内外净资产的规模变化及其所进行的冲销操作情况。自2001年加入WTO以来,中国的经常账户与资本账户“双顺差”规模迅速扩大,导致中国央行持有的国外净资产规模急剧增加。从2002年到2010年,国外净资产绝对值从17510.54亿元增加到188670.61亿元,增长了9.77倍,国外净资产与基础货币的比例也从0.49上升到1.07,峰值为2007年年中的1.24。与此相对应,国内净资产绝对值从2002年初的21512.86亿元下降到2010年末的-26632.50亿元,与基础货币的比例从0.49下降到-0.22,峰值为2009年年末的-0.37。从变化量来看,在全部样本期的107个月中,73个月中ΔNFA与ΔNDA的符号相反,其中68个月ΔNFA为正而ΔNDA为负,表明央行大部分时期都在对冲外汇储备过多引发的流动性过剩。可见,2002年以来,针对国外净资产的被动性快速增加,中国央行较为显著地主动调整其资产负债结构,国内净资产不断下降,使之与国外净资产呈反向走势,以抵消国外净资产的增加对于基础货币的影响。总的来看,中国央行进行了较为充分的冲销操作。
(三)冲销系数的估计与回归分析
现有文献对于冲销系数的估计方法主要包括普通最小二乘法(OLS)、联立方程模型以及向量自回归模型(VAR模型)。VAR模型的主要缺陷在于难以观测到即期冲击的响应,而联立方程模型主要是为了解决OLS法可能存在的变量内生性问题。在本文中,考虑到冲销操作的即期冲击效应较为明显故未采取VAR模型,而对ΔNDA和ΔNFA数据进行Hauseman检验后认为并不存在内生性问题,此时OLS法的效果更好,因而本文采取OLS法进行回归分析。
表3 回归分析结果
|
因变量 |
自变量 |
所有变量(回归①) |
剔除不显著变量(回归②) |
剔除线性相关及不显著变量(回归③) |
剔除线性相关及不显著变量(回归④) |
|
ΔNDA |
c |
0.01019*** (4.15178) |
0.00925*** (3.93240) |
0.00729*** (3.36707) |
0.01221*** (5.45750) |
|
ΔNFA |
-0.59989*** (-7.39217) |
-0.55776*** (-7.37118) |
-0.55825*** (-7.02534) |
-0.62705*** (-7.71584) | |
|
ΔNFA(-1) |
-0.22032*** (-2.72947) |
-0.17940** (-2.33559) |
-0.14558 (-1.91388) |
-0.22990*** (-2.96150) | |
|
ΔNFA(-2) |
-0.13321* (-1.69606) |
-0.16825** (-2.22268) |
-0.09843 (-1.26961) |
-0.18055** (-2.25526) | |
|
Δmm |
-0.19049*** (-18.35524) |
-0.19387*** (-20.35134) |
-0.19635*** (-20.41663) |
-0.18952*** (-19.51799) | |
|
Δp(-1) |
-0.55553*** (-3.49526) |
-0.53298*** (-3.51578) |
-0.49496*** (-3.248180) |
-0.52262*** (-3.33268) | |
|
Δreer |
-0.12555 (-1.45998) |
|
-0.143076* (-1.66787) |
-0.16373* (-1.89036) | |
|
Δre(-1) |
-0.04126 (-1.25675) |
|
|
| |
|
gap(-1) |
-0.00221*** (-2.88973) |
-0.00229*** (-3.23137) |
-0.00286*** (-4.47637) |
| |
|
Δg(-1) |
-0.71828 (-0.86066) |
|
|
| |
|
Δhouse(-1) |
0.15702** (2.28575) |
0.164129** (2.42110) |
|
0.24691*** (3.99221) | |
|
冲销系数 |
-0.95341*** |
-0.90542*** |
-0.80227*** |
-1.03749*** | |
|
|
(-8.31590) |
(-8.20623) |
(-8.06444) |
(-9.86556) | |
|
R2 |
0.82314 |
0.82147 |
0.815961 |
0.80928 | |
注:“***、“**”、“*”分别表示在1%、5%、10%的水平上是统计显著的。
考虑到月度数据的政策滞后效应可能较为明显,在OLS回归中直接加入自变量的滞后项又可能导致估计结果的偏差,故本文采用阿尔蒙多项式分布滞后模型对ΔNFA及其滞后项的系数进行估计。具体设置上,我们选择一个季度为政策响应的周期,即估计的最大滞后期为两期,且响应系数设定为二次型系数。也正是由于月度数据存在较为明显的滞后效应,我们将每期的冲销系数定义为回归方程中ΔNFA的即期、滞后1期、滞后2期的三个系数之和。结合理论分析结果,本文的实际回归方程为:
ΔNDAt=μ0t-(β0ΔNFAt+β1ΔNFAt-1+β2ΔNFAt-2)-μ2tΔmmt-μ3tΔpt-1-μ4tΔreert-μ5tΔret-1-μ6tgapt-1-μ7tΔhouset-1
其中β按照阿尔蒙二项式分布定义为:
βi=α0+α1i+α2i2,i=0,1,2。
冲销系数定义为STER=β0+β1+β2=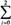 βi。
βi。
1、对全样本期的整体回归
回归结果如表3所示。在对所有变量的整体回归结果中,为检验回归结果的稳健性,本文在对所有变量回归的基础上依次根据t值剔除了回归结果中最不显著的变量以及根据相关系数先后分别剔除了线性相关度较高的gap和Δhouse变量,得出了表3中的回归结果。资产价格代理变量Δhouse的系数符号与理论模型预测相反,这可能与央行对资产价格是否具有泡沫成分的判断、政策反馈时间较长以及货币政策在应对资产价格波动方面是一种“迟钝”的工具有关,其他变量均符合理论模型的预测。根据表3中的回归②到回归④的结果,可以看出各变量的回归系数均较为显著,且与回归①相比估计值变化不大。例如在各回归结果中Δmm参数估计值的变动区间为-0.18952—-0.19635,Δp参数值的变动区间为-0.49496—-0.55553,调整后的R2在0.809—0.823之间变化,冲销系数在-0.8—-1之间变化,均表明回归结果具有较高的稳健性。
从冲销系数来看,中国央行进行了相当充分的冲销操作。图4显示了中国央行对于即期及滞后期国外净资产增量的冲销力度的变化,与回归结果中反映的趋势相同:即冲销操作对即期冲击响应最大,随着滞后期的延长冲销效应逐渐趋弱。其中,对ΔNFA即期变化的冲销系数约为-0.55—-0.63,对其滞后1期的冲销系数约为-0.15—-0.23,对其滞后2期的冲销系数约为-0.1—-0.18。这表明,中国央行近年来的冲销操作具有较好的及时性和灵活性。
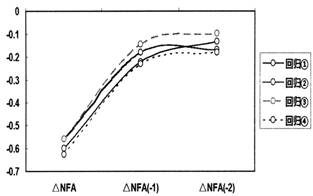
图4 对外汇占款增量(ΔNFA)各滞后期的冲销系数
2、以24个月为周期的滚动回归
为了进一步研究中国央行进行货币冲销操作力度的动态变化及其对国内经济产生的影响,本文在对全样本期整体回归后进行了以24个月为周期的滚动回归。与之前相关研究文献不同的是,本文认为将从第t-23期到第t期样本回归作出的冲销系数反映的是这一时间区间内的平均水平,以此作为第t期这个时点的冲销系数未必科学。本文采取的方法是将第t-23期到第t期回归往后依次滚动到第t期到第t+23期,将得出的24个冲销系数的平均值作为第t期的冲销系数,最后23期数据不足但信息已经包含在之前的平均冲销系数中,故采用自回归方法预测形成,最终得到2004年4月至2010年12月的冲销系数STER(图5)。
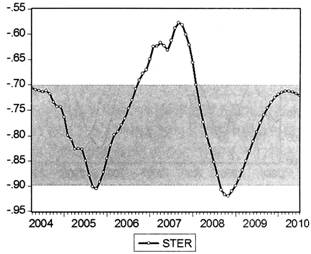
图5 24月为周期滚动回归得出的动态冲销系数
从图5中可以看出,近年来中国央行的冲销系数基本在-0.7—-0.9之间波动,可以说对不断攀升的国外净资产进行了比较充分的冲销操作。具体来看,冲销系数的动态变化具有两个特点:一是虽然整体上冲销力度较为充分但也并非一成不变,主要表现为在一定区间内呈现向均值回归的波动态势,我们很难区分这种波动究竟是央行的主动行为还是迫于多方面被动因素考虑后的无奈选择,但其对国内经济的影响却是值得我们重点关注的;二是在2006年至2007年期间冲销系数大幅上升形成一个异常突出的波峰(亦即冲销系数绝对值大幅下降,冲销力度大幅削弱),下面我们将重点考察这次波峰出现的成因和经济后果。
四、中国货币冲销操作对宏观经济的影响
按照货币冲销程度对宏观经济的影响机制,本文选取基础货币增速(MB)、实际同业拆借利率(REALCHIBOR)、产出缺口(GAP)、消费物价指数(CPI)来研究央行冲销操作对国内宏观经济的影响。其中MB为基础货币增速经年度移动平均去除季节因素后得到,REALCHIBOR的计算方法为: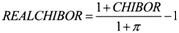 ,CHIBOR为年化名义同业拆借利率,π为以CPI为表征的年度通胀率。
,CHIBOR为年化名义同业拆借利率,π为以CPI为表征的年度通胀率。
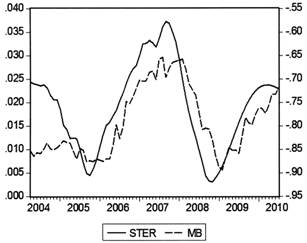
图6 动态冲销系数(STER)与基础货币增速(MB)
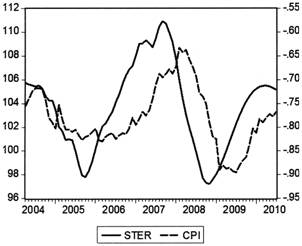
图7 动态冲销系数(STER)与CPI
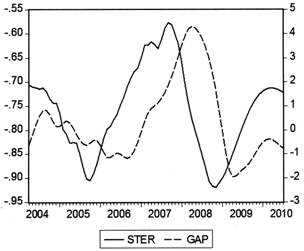
图8 动态冲销系数(STER)与产出缺口(GAP)
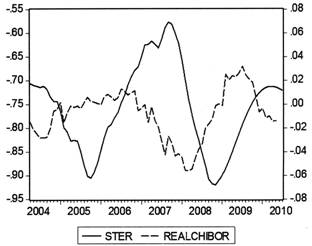
图9 动态冲销系数(STER)与实际同业拆拆借利率(REALCHIBOR)
动态冲销系数STER与各经济变量间关系如图6至图9所示。可以看出,冲销系数是各经济指标非常好的先行作用因素,作用时滞一般在4—14个月之间,且作用方向符合理论:冲销系数上升,即冲销系数绝对值下降、冲销力度减弱时,基础货币增速加快、实际同业拆借利率水平随之下降、产出缺口上升为正且逐步扩大、物价水平上涨加快。具体而言,2004年到2005年期间中国央行的冲销力度逐渐加大,较好地抵消了国外资本流入对中国基础货币的冲击,使基础货币增速在这两年间保持相对平稳,实际同业拆借利率和产出缺口也波动较小,物价水平呈整体小幅下降的趋势;2006年开始冲销力度大幅下降直到2008年中期才回复到均值水平,这一轮冲销力度的下降很快促使基础货币增速飙升,继而伴随实际同业拆借利率水平的下降、产出缺口的显著增大以及物价水平的连续冲高;2008年中期开始冲销系数逐渐回复至正常区间波动,直到2009年中后期开始持续至2010年上半年冲销力度再次趋弱,这也带来了基础货币增速、产出缺口和物价水平的相应上涨,只是幅度并没有2006—2007年期间那么剧烈。
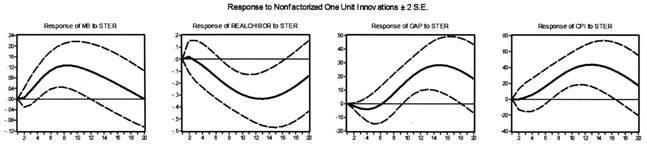
图10 VAR模型中各变量对冲销系数的脉冲响应
为了定量分析冲销系数与其他变量间的动态相互作用,我们将这些变量建立起一个向量自回归(VAR)模型,滞后期根据SIC规则选择为2,且通过单位根稳定性检验。首先基于这样的VAR系统进行格兰杰因果检验(表5),结果表明,冲销系数在该动态系统中均构成了其他经济变量的格兰杰原因,且与基础货币增速之间的格兰杰因果关系最为明显。其次,观察各经济变量对1单位冲销系数变化所产生的脉冲反应,结果如图10所示,冲销系数对各经济变量的影响与前面的描述一致,作用方向均符合理论设想,对基础货币作用最快,在6—8月达到作用峰值,对实际同业拆借利率的作用在12个月左右达到峰值,对产出缺口和物价水平的作用在14个月左右达到峰值,这也符合之前所述的经济变量传导的逻辑顺序。
表5 基于VAR模型的格兰杰因果检验
原假设:冲销系数STER不是A的格兰杰因
|
因变量(A) |
MB |
REALCHIBOR |
GAP |
CPI |
|
p值 |
0.002*** |
0.050** |
0.071* |
0.086* |
注:“***”、“**”、“*”分别表示在1%、5%、10%的水平上是统计显著的。
五、货币冲销系数动态变化的影响因素分析
在考察了冲销水平的变化对经济产生的影响后,我们进一步从冲销成本因素和国内净资产调整规模限制因素两个方面,分析中国央行冲销水平波动的原因。
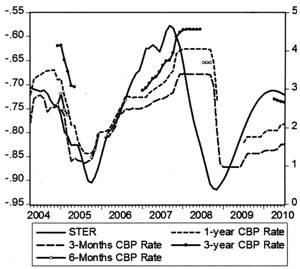
图11 动态冲销系数与央行票据发行利率
责任编辑:夏雨

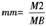

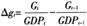
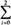 βΔNFA(-i)
βΔNFA(-i)