含有变结构点的面板循序检验方法研究

内容提要：针对含有变结构点的面板数据易产生“伪单位根”现象，提出面板循序检验方法：首先给出检验模型和检验步骤，其次通过Monte Carlo模拟得到检验统计量的临界值，最后结合我国各地区的GDP数据进行实证分析。研究发现：中国GDP数据为带有结构突变的趋势平稳序列。
    关键词：面板数据 变结构点 循序检验 单位根
    作者简介：陈海燕(1982-)，女，重庆人，博士生，研究方向：计量经济学，非参数统计；杨宝臣(1966-)，男，河北唐山人，教授，博士生导师，研究方向：经济与金融的计量方法。天津大学管理学院（天津300072）
    引言
    经济结构随着国家政策和经济运行的环境变化而变化。当重大的经济政策和制度发生变化，重大的政治革命发生，重大的技术革命和技术创新发生时，均可能导致经济结构的变化。因此，分析社会经济系统不能只局限在不变的系统之中，必须考虑经济系统建模中变结构问题。序列结构上的突变常常会使得单位根检验的功效降低，将具有结构突变的平稳序列误判为非平稳的单位根过程，产生“伪单位根”现象，还将导致对序列协整关系的误判。
    时间序列变结构问题的研究是经典计量经济学研究的一个重要问题，涉及变结构点的检测、变结构协整问题、变结构模型的建立和应用等方面。面板数据是在时间序列上取多个截面，并在这些截面上同时选取样本观测值所构成的数据形式，能多方位的反映数据信息，提供更大的自由度和更高的估计效率。近年来对于面板数据模型的研究已在国内外掀起一股热潮，其研究领域也逐步扩大。面板数据变结构模型即是研究面板数据的变结构问题，这不仅将传统时间序列里存在的变结构问题进行了深化，而且扩大了数据研究形式，更能适应经济社会发展的需要，更能体现经济金融市场上的变化。面板数据的变结构问题直接影响着面板数据单位根检验的有效性和协整检验的准确性。
    对于面板数据变结构问题的研究与应用是非平稳面板计量经济学的重要内容。Emerson和Kao对波动检验和Wald检验进行了扩展，提出适合检验面板数据变结构的统计量，给出了统计量的极限分布和临界值表，并用提出的检验方法对OPEC国家等的GDP、消费增长和生产率增长进行了变结构检验[1,2]。Han和Park提出了适合面板数据变结构模型的CUSUM检验[3]。Schroeter和Fenn应用面板数据CUSUM检验对香烟需求进行了变结构检验[4]。Perron提出当时间序列的变结构点已知时，在ADF检验式中加入描述结构突变的虚拟变量可以检测原序列是否为单位根序列[5]。他还研究了变结构点未知的情况，对去势处理后的序列进行ADF检验，同时对所有可能的变结构点重复进行这一过程来判断原序列是否为单位根序列[6]。Banerjee、Lumsdaine和Stock采取在原样本范围内连续抽取不同子样本的方式提出3种含有结构突变点的单位根检验方法：递归检验、滚动检验和循序检验[7]，3种检验方法得到的都是一个单位根检验统计量值的序列，并从中选择最小的一个值与临界值比较，从而判断原序列为单位根过程还是带有结构突变的趋势平稳过程。
    在建立变结构模型时，如果已知变结构点则可以快而准的给出模型形式，如果变结构点未知，只能对模型中所有可能的结构突变点进行检验对比，所以变结构点是否已知对于变结构模型的建立起着至关重要的作用。
    一、含有变结构点的面板循序检验
    
    50，模拟次数H=10000，对序列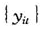按照(1)式的形式进行估计得临界值如表1。
    表1临界值表
    
    比如对于N=10，T=25，根据数据生成过程式(3)得到面板数据序列，首先可考虑a=0.15，b=0.85时，确定结构突变的时间范围为[3,23]，让t分别在区间[3,25]，[4,25],…,[22,25]内循序取值，对式(1)进行估计，得到系数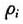的t统计量值的平均值序列，从而得到序列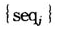，j=1,…,20。如此循环10000次，就可以得到当N=10，T=25时不同显著性水平下变结构点的临界值。
    相对于Banerjee、Lumsdaine和Stock研究中时间序列数据变结构循序检验的临界值，本文模拟得出的面板数据变结构循序检验的临界值稍微大一些，主要原因在于面板数据的特殊数据形式，它将截面数据和时间序列数据相结合，从而具有更大的自由度，提供更为详细的数据信息，在数据形式上划分更为具体。
    三、实证研究
    下面将结合中国各地区的GDP数据对上述检验方法进行实证分析。面板数据样本区间为1992～2005年，截面个数为30（除了重庆外，包括全国其余30个省份），单位为亿元，数据按照当年价格计算。图1给出了30个省份GDP数据的图形，整体而言，各地区GDP每年都有上升趋势。
    
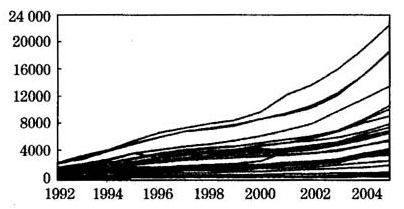
    图1各地区GDP数据图
    
    表2面板单位根检验表
    
    
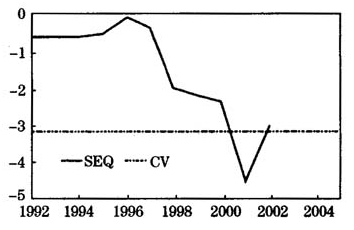
    图2序列变结构点检验得到的序列图
    
    四、结论
    针对含有变结构点的面板数据单位根检验问题，本文结合时间序列变结构点检验的循序检验方法，提出了含有变结构点的面板循序检验，并通过Monte Carlo模拟给出部分样本的临界值，最后应用此检验方法对中国30个省份的面板数据序列GDP进行了实证分析。对1992～2005年样本区间内的GDP序列进行传统面板单位根检验，发现GDP序列为非平稳面板序列，但通过变结构循序检验得出GDP序列实为带有结构突变的趋势平稳序列，且2001年为变结构点。
    参考文献：
    [1]Emerson J, Kao C. Testing for structural change of a time trend regression in panel data: part I [J]. Journal of Propagations in probability and statistics, 2001, 2 (1): 57-75.
    [2]Emerson J, Kao C. Testing for structural change in panel data: GDP growth, consumption growth, and productivity growth [J]. Economics Bulletin, 2006, 3 (14):1-12.
    [3]Hah A K, Park D. Testing for structural change in panel data: application to a study of U. S. foreign trade in manufacturing goods [J]. The Review of Economics and Statistics, 1989, 71 (1): 135-142.
    [4]Schroeter J, Fenn A. Structural change in cigarette demand: CUSUM tests using panel data [J]. Economics Bulletin, 2005, 9 (8):1-11.
    [5]Perron P. Testing for a unit foot in a time series regression with a changing mean [J]. Journal of Business and Economic Statistics, 1990, 8 (2):153-162.
    [6]Perron P. Further evidence on breaking trend functions in macroeconomic variables [J]. Journal of Econometrics,1997, 80 (2): 355-385.
    [7]Banerjee A, Lurmsdaine R L, Stock J H. Recursive and sequential tests of the unit-root and trend-break hypothesis: theory and international evidence [J]. Journal of Business and Economic Statistics, 1992, 10 (1): 271-287.