基于稳健主成分回归的统计数据可靠性评估方法（下）

（二）数据处理
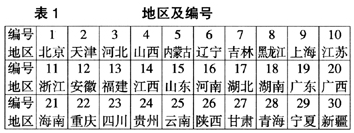
    本文以2008年我国地区横截面数据为例，说明稳健主成分回归方法在数据可靠性评估方面的应用。为此，本文搜集了2007年和2008年各地区的经济增长以及前文所述的12个指标的数据，除银行信贷数据来源于相应年份的《中国金融年鉴》外，其他的数据都来源于《中国统计年鉴》。由于西藏缺失电力消费数据，未列入本文的分析，因此，实际列入本文分析的有30个地区，各地区及其相应的编号见下页表1。
    
    对于搜集到的数据，还需要将其转化为增长率的形式。对于2008年各地区的环比地区生产总值指数，本文直接将其减100，即得到各地区的经济增长率数据；对于其他表现为绝对数的总量指标，本文用2008年的数据除以2007年的数据减去1再乘以100的方法②。由于按现价计算的价值指标所求得的增长率都是名义增长率，因此，有必要对其调整，消除数据中通货膨胀的影响。本文用美国的消费价格指数（CPI）对各地区出口额的名义增长率进行调整，用各地区的生产者价格指数（PPI）对银行信贷名义增长率进行调整，用各地区的CPI指数对其他价值指标的名义增长率进行了调整。最终整理出各地区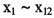各指标相对应的增长率数据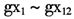（单位：%），各地区经济增长率（y）以及相关指标增长率（）。
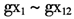    四、诊断结果及分析
    根据前文所选的2008年30个地区的横截面数据集，本文以地区经济增长（y）为因变量，以12个相关指标的增长率（）为自变量，运用基于稳健主成分回归（RPCR）的异常值诊断方法对地区经济增长数据的可靠性进行评估，并与经典的主成分回归分析（CPCR）诊断结果进行比较。在分析的过程中，由于事先并不知道数据集中异常数据的可能比例，本研究直接将可能包含的异常值的比例设为允许的最高限50%。利用Matlab软件稳健分析工具箱LIBRA，进行稳健主成分回归及诊断的步骤如下。
    （一）稳健主成分分析及主成分空间异常值诊断结果
    1.稳健主成分分析及主成分数目的选择
    稳健主成分回归分析的第一步是进行稳健主成分分析（ROBPCA），并选择最优数目的主成分。
    如果研究的目的只是进行主成分分析，可以直接根据主成分的方差贡献率和碎石图来选择主成分的数目。然而，本文的目的是进行稳健主成分回归，还要考虑所选主成分对因变量的预测能力和拟合能力。因此，本文根据前文介绍的稳健主成分选择统计量（下称RCS）选择最优主成分数目。根据前文提供的各相关指标增长率的数据集，使用Matlab软件的RPCR函数可直接绘制当γ=0，0.5和1时的RCS曲线图，见图1。
    
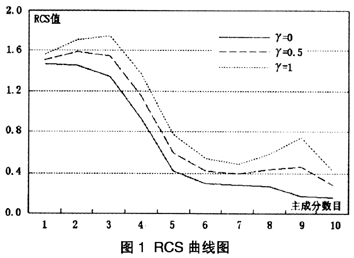
    由图1可见，当k=6时，RCS曲线变得较为平缓，并且当k=6时与k=10时的预测误差差异很小。为了避免维度诅咒问题，一般建议n＞5k[8]，因此，在ROBPCA中本文选择保留6个稳健主成分，这6个稳健主成分的方差贡献达97.57%。同时，为便于对比，在CPCA中也选择保留了6个主成分。
    2.主成分空间异常值的诊断
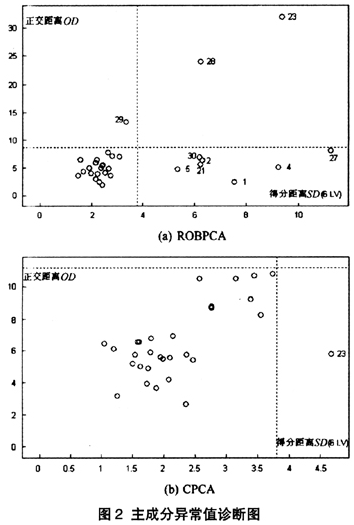
    在ROBPCA以及CPCA分析过程中，可以使用正交距离OD对得分距离SD诊断图识别出主成分空间的异常值，两种方法得分距离SD的临界值都为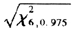=3.80；但正交距离OD的临界值不同，ROBPCA分析中正交距离OD的临界值为8.63，CPCA分析中正交距离的临界值为11.21。超过这些临界值的点可被诊断为主成分异常点。ROBPCA以及CPCA诊断图见图2（a）、（b）。
    由图2（a）ROBPCA诊断图可见，四川（23）、青海（28）等省份的相关指标增长率数据被诊断为坏的主成分杠杆点，这些观测值对CPCA有很大的破坏作用；宁夏（29）的相关指标数据被诊断为正交异常值，这一数据点距主成分子空间的正交距离很大，但对CPCA没有影响；而北京（1）、天津（2）、山西（4）、海南（21）、甘肃（27）和新疆（30）等省份的数据被诊断为好的主成分杠杆点，这些观测值虽然远离正常观测值，但其距主成分子空间的距离很近；除此之外，其他省份的数据都是正常观察测值。与之相比，由于受异常值本身的影响，CPCA诊断图仅识别出四川（23）的数据为好的主成分杠杆点（见图2（b）），而其他省份相关指标的数据都为正常观测值。可见，ROBPCA方法能更好地诊断出主成分空间的异常值。
    
    （二）稳健主成分回归及异常值诊断结果
    1.稳健主成分回归结果及分析
    稳健主成分回归分析（RPCR方法）的第二步是在由ROBPCA提取的稳健主成分的基础上，进一步运用稳健的LTS估计方法，将因变量对主成分得分进行回归，以克服异常值对估计结果的影响。根据上文所选的6个稳健主成分，可计算稳健主成分得分变量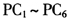，并进一步运用稳健的LTS估计方法，将经济增长率（y）与这些主成分得分变量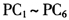（）进行回归分析，并得到稳健回归结果，见表2③。作为比较，表2同时给出了由CPCA保留6个主成分时，进一步使用OLS估计方法得到的CPCR估计结果。
    
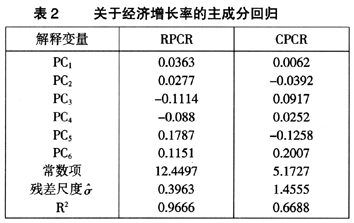
    由表2可见，由LTS估计得到的稳健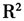达0.9666，稳健LTS回归模型拟合效果很好，说明这些主成分得分对经济增长率有很强的解释能力。相比之下，受可能存在的异常值的影响，由OLS估计得到的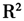只有0.6688④。
    为了验证经济增长率与各相关指标是否匹配，根据稳健主成分特征向量及上述回归系数，将这些系数还原为各相关指标增长率的系数（即经济增长率对各相关指标的偏导数，也是地区生产总值对各相关指标的弹性），具体见表3。作为比较，表3也列出了使用CPCR方法且保留6个主成分时，最后还原得到的各相关指标增长率的系数。
    
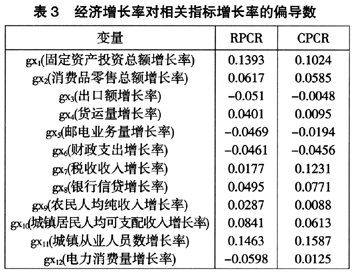
    由RPCR分析结果可见，除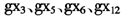等指标外，其余各指标增长率的系数均为正，符合经济学的规律。出口增长率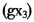的系数为负，反映了2008年我国受国际金融危机影响，外部需求显著减少、出口明显下滑，经济增长主要靠内需拉动的现实；邮电业务增长率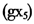的系数为负，可能是由于该指标存在测量误差，近年来，随着现代信息技术的快速发展，邮电业务的形式发生了很大改变，而邮电业务的统计口径却仍保持不变；财政支出增长率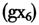的系数为负，可能原因是2008年重大自然灾害频繁发生，为应对灾害，受灾地区财政支出增长较快，而灾害对地区经济增长也具有一定负面影响；电力消费增长率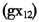的系数为负，说明2008年我国地区电力消费增长与经济增长率出现不同步现象，这也是包括华尔街日报、国际能源署在内的一些境内外媒体和国际组织对中国经济数据可信度质疑的原因之一，国家能源局（2009）从产业结构变化、高载能产品“去库存化”、产业能耗下降等方面对此现象做了解释说明[9]。总之，基本可以认为地区经济增长数据与相关指标数据是匹配的。
    CPCR的分析结果中，除电力消费增长率之外，其余各指标增长率系数的符号都与RPCR的分析结果相同。然而，这些系数的大小不尽相同，有些差异还比较大，如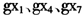等。相比之下，由于RPCR考虑了数据中可能存在的异常值的影响，其分析结果相对更加可靠。
    2.稳健主成分回归中异常值诊断结果及分析
    
    
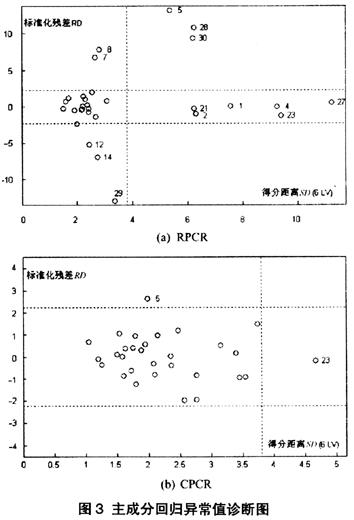
    由图3（a）RPCR残差诊断图可得如下结论：北京（1）、天津（2）、山西（4）、海南（21）、四川（23）、甘肃（27）等地区的得分距离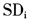都超出了临界值，但其标准化残差绝对值很小，这些地区的数据被诊断为好的杠杆点；内蒙古（5）、青海（28）、新疆（30）等地区的得分距离和标准化残差绝对值都很大，因此可看作是坏的杠杆点；吉林（7）、黑龙江（8）、安徽（12）、江西（14）、宁夏（29）等地区的得分距离虽然很小，但其标准化残差绝对值都很大，因此可看作是纵向异常点；其余地区的数据可看作是正常观测值。相比之下，由图3（b）CPCR诊断图可见，只有四川（23）被诊断为好的杠杆点，内蒙古（5）被诊断为纵向异常点。可见，由稳健的RPCR方法克服了异常值的影响，诊断出了更多的异常值，可以有效地解决基于经典的CPCR的诊断方法容易出现的多个异常点的掩盖现象。
    结合异常值产生的背景，对2008年各地区经济增长数据的可靠性进行判断。根据稳健的RPCR的诊断结果，北京（1）、天津（2）、山西（4）、海南（21）、四川（23）、甘肃（27）等地区的稳健得分距离虽然被诊断为异常点，但这些地区的数据对模型拟合得很好，因此，可以认为这些地区的经济增长数据是可靠的；内蒙古（5）、青海（28）、新疆（30）等地区的数据被诊断为坏的杠杆点，这些地区的得分距离和标准化残差都表现为异常，这一方面可能是这些地区的经济增长及相关指标数据的可靠性存在问题。另一方面有可能与这些地区的特殊发展背景有关，如自2002年以来内蒙古经济增速蝉联我国第一，“内蒙古现象”全国瞩目。2008年内蒙古经济增速达17.2%，与其能牢牢抓住产业转移机遇，把自然资源禀赋比较优势化为竞争优势等多方面的因素有关；吉林（7）、黑龙江（8）、安徽（12）、江西（14）、宁夏（29）等地区的数据被诊断为纵向异常点，说明在现有的数据集中，这些地区经济增长数据的可靠性可能存在问题。其中，吉林（7）、黑龙江（8）等地区的经济增长数据可能被高估，而安徽（12）、江西（14）、宁夏（29）等地区的经济增长速度数据反而有被低估的可能。
    五、结论
    总结全文，本文首先介绍了Hubert和Verboven（2003）提出的稳健主成分回归（RPCR）及相应的异常值诊断方法，然后选取了理论上与经济增长相关的12个指标，运用RPCR方法对2008年我国地区经济增长横截面数据的可靠性进行了评估，并将评估结果与经典的主成分回归（CPCR）方法的结果进行了比较。研究结果表明：①稳健的RPCR方法能更好地克服异常值的影响，估计结果相对更加可靠，并诊断出了更多的异常值，有效地解决了基于经典的CPCR的诊断方法容易出现的多个异常点的掩盖现象；②根据RPCR的估计结果以及异常值诊断结果，并结合2008年的具体背景，基本可以认为2008年地区经济增长数据与相关指标数据是匹配的，但是部分地区的经济增长数据可能存在可靠性问题。经济增长数据的可靠性评估是一个非常复杂的问题，本文所做的研究为相关部门及时掌握有关信息提供了可供选择的工具。
    注释：
    ①LIBRA是包含了包括RPCR等诸多稳健统计方法在内的Matlab程序工具库，由比利时鲁汶大学数学系和安特卫普大学数学和计算机科学系的稳健统计研究组开发。LIBRA可从以下网址下载：http://wis.kuleuven.be/stat/robust/.
    ②本文没有采用对数差分求近似增长率的做法，因为对于很小的变化，变量的增长率相当于对变量做对数差分处理，而对于有较大变化的变量，对数差分求得的增长率误差较大。
    ③虽然可以由加权的LTS估计得到如系数的t统计量等推断结果，但其对应的P值只是近似的，通常并不知道该P值是否是真实。因此，这里仅输出了LTS回归的系数，没有给出各系数对应的t统计量。
    ④由ROBPCA估计得到的主成分得分和由CPCA估计得到的主成分得分是不一样的，因此，直接比较LTS和OLS两种方法估计得到的主成分得分变量的系数并没多大意义。
    参考文献：
    [1]Klein, L. R. and Ozmucur, S. The Estimation of China's Economic Growth[J]. Journal of Economic and Social Measurement, 2002(28): 187-202.
    [2]阙里，钟笑寒.中国地区GDP增长统计的真实性检验[J].数量经济技术经济研究，2005(4)：2-12.
    [3]Hubert, M., Verboven, S. A Robust PCR Method for High-dimensional Regressors[J]. Journal of Chemometrics, 2003(17): 438-452.
    [4]Hubert, M., Rousseeuw, P. J., Vanden Branden, K., ROBPCA: A New Approach to Robust Principal Components Analysis[J]. Technometrics, 2005(47): 64-79.
    [5]Rousseeuw, P. J. Least Median of Squares Regression[J].Journal of the American Statistical Association, 1984(79): 871-880.
    [6]Pison, G., Van Aelst, S. and Willems, G. Small Sample Corrections for LTS and MCD[R]. Metrika, 2002(55): 111-123.
    [7]Engelen, S. and Hubert, M. Fast Model Selection for Robust Calibration Methods[J]. Analytica Chimica Acta, 2005(544): 219-228.
    [8]Rousseeuw, P. J. and van Zomeren, B. C. Unmasking Multivariate Outliers and Leverage Points[J]. Journal of the American Statistical Association, 1990(85): 633-651.
    [9]国家能源局.能源消费与经济增长不同步的分析[OL].http://www.stats.gov.cn/tjfx/fxbg/t20090610_402564397.htm，2009.