随机系数离散值时间序列模型（下）

    
    从表1的模拟结果可以看出，对于五种密度函数的每一种类型样本均值与真实值都相差不大，同时相对误差MAPE与均方根误差RMSE也比较小。下面以（α＜1，β＜1）这种情况为例，进行详细阐述。它的最高绝对偏差是0.0200、最低绝对偏差是0.0040，无论哪一个值都与真值3差别不大；同时相对误差MAPE最高为0.1109、均方根误差RMSE最高为0.4068，说明这些估计值的波动范围不大，大都落在真值3附近。从样本容量来看，随着样本容量的增大越来越接近于真实值，因为Bias一直在减少。同时随着样本容量变大，波动范围也在迅速变小，因为MAPE与RMSE的减少幅度较大。例如RMSE，当样本容量从50变到100时，RMSE的取值减少了27.21%；当样本容量从100变到300时，RMSE的取值减少了49.67%。对于同一样本容量，例如N=100时，随着Beta参数（α，β）的变化，这四个统计指标、Bias、MAPE、RMSE都无明显规律性。关于对于（α，β）取值的其他情况，都和（α＜1，β＜1）情况差不多，不再赘述。根据表1的结果可推知：无论哪一种密度函数，Bias、MAPE、RMSE都较小，说明从偏差与波动程度来看，受（α，β）取值的影响程度较小。
    从表2可以看出，对于同一样本容量，随着滞后阶数q的增大，Bias的取值比较小，但它的变化无明显规律性；而MAPE与RMSE的取值均较小，不过它们一直在增加，但增加的幅度不大。例如样本容量N=100时，Bias的绝对值最大的是0.0324，说明估计结果离真值相当近；样本容量N=100时Bias取值正负都有，其绝对值的大小随着q的增加既有变大又有变小，无明显趋势。样本容量N=100时，MAPE的取值为0.0671、0.0760、0.0843、0.0963、0.1055，说明估计量的波动程度相当小；随着滞后阶数的增加，它的增加幅度依次为13.26%、10.92%、14.23%、9.55%，以上数字说明MAPE的增加幅度不大。由于RMSE的增加情况与MAPE类似，不再赘述。根据表2的结果可知：对于不大的滞后阶数，Bias都相当小，体现波动程度的MAPE与RMSE从绝对量来看也较小，所以滞后阶数的不同对估计结果影响也较小。
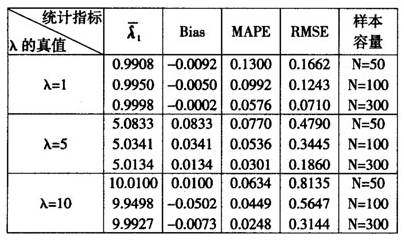
    从表3可以看出随着λ变大，对于相同样本容量的估计量：Bias的变化并无规律；MPAE在一直减小；RMSE在一直增大。Bias有时增大、有时减小，例如对于样本容量N=50时，Bias的绝对量先从0.0092增加到0.0833，再减小到0.01；而N=100时，Bias的绝对量一直在增加，先从0.005增加到0.0341，再增加到0.0502。而MAPE减少的幅度先大后小，例如N=300时MAPE减少的幅度为47.74%、17.60%，N=50时MAPE减少的幅度为40.76%、17.66%。RMSE的增加幅度均较大，例如N=100时RMSE增加的幅度为177.15%、63.91%，N=50时RMSE增加的幅度为188.21%、69.83%。此外对于相同的λ，随着样本容量的增加，Bias、MPAE、RMSE均一直减小。根据表3的结果可知：对于常用的不大的λ值，偏差Bias都比较小，波动程度MAPE与RMSE从绝对量来看也较小，所以λ的不同对估计结果影响也较小。
    综合表1、表2和表3的结果可知，本文得到的一致估计量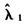的小样本性质、大样本性质均较好；无论从随机系数密度函数的变化、滑动平均滞后阶数的变化、样本容量大小的变化与参数λ取值的变化来看，估计量的误差均较小，说明估计结果比较稳健。在定理5中的其余三个估计量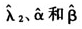也有类似结果，限于篇幅，不再赘述。
    五、结论
    最近30年来，关于离散值时间序列的国外文献资料汗牛充栋。国外学者大多从事理论研究，具有一定深度；而国内大多集中在实证研究上，理论研究的深度和广度都很欠缺。国内外的研究热点主要集中在参数估计、平稳性与模型定阶上。
    本文的主要工作在于推广了q阶固定系数整值滑动平均模型，允许系数是随时间（或者指标t）变化而变化的Beta分布的随机变量。得到该随机过程的一维分布与一、二阶矩，证明了该随机过程是宽平稳过程，均值与协方差具有遍历性，求得了系数的矩法估计，并证明了矩法估计具有遍历性。模拟结果显示估计量的统计性质较好。
    连续时间序列模型的定阶处理比较完善，但离散值时间序列的模型定阶是一个公开的问题，具有一定难度。而随机系数的模型定阶则更复杂，故这个问题是以后研究方向之一。现在大多数国外文献热衷于理论研究，实际应用的案例较少，特别是证券与金融的相关案例更少。如何结合实际数据改造现有模型是一个值得注意的研究方向。统计模型还有一个大的内容是参数的检验，在离散值时间序列中这类文献很少，应该是理论界关注的重点。
    参考文献：
    [1]Mardia. Some results for dams with Markovian inputs[J]. Stoch. Proc. And Appl, 1973(8):199-209.
    [2]Harvey, A.C. and C. Fernandes. Time series models for count or qualitative observations[J]. J. Bus. Econ. Statist, 1989(7):407-422.
    [3]Hujer, Reinhard, Vuletic, Sandra and Kokot, Stefan. The Markov Switching ACD Model[J/OL]. www.ssrn.com, 2002.
    [4]Ferland, Rene, Latour, Alain and Oraichi, Driss. Integer-Valued GARCH Process[J]. J. Time Series Anal, 2006,27(6):923-942.
    [5]Andersson J. and Karlis D. Treating missing values in INAR(1) models: An application to syndromic surveillance data[J]. J. Time Series Anal, 2010,31(1):12-19.
    [6]Al-Osh M. and Alzaid A. Integer-Valued Moving Average (INMA) Process[J]. Statistical Paper, 1988(29):281-300.
    [7]Brannas, K. and Quoreshi, A.M.M.S. Integer-Valued Moving Average Modelling of the Number of Transactions in Stocks[J]. Applied Financial Economics, 2010(20):1429-1440.
    [8]Zheng, H.T., Basawa, I.V., Datta, S. Inference for pth order random coefficient integer-valued autoregressive processes[J]. J.Time Series Anal, 2006(27):411-440.
    [9]Steutal, Van Harn. Discrete analogues of self-decomposability and Stability[J]. Ann. Prohab, 1979(7):893-899.
    [10]Thmas A, Severini. Elements of Distribution Theory[M]. Cambridge University Press, 2005.
    [11]Brockwell, P.J. and R.A. DavisTime Series: Theory and Methods. 2nd[M]. Springe-Verlag, 1991.
    [12]Samuel Karlin and Howard M. Taylor. A First Course in Stochastic Process[M]. Academic Press, 1975.
    [13]Victor Enciso-Mora, Peter Neal and Tara Subba Rao. Efficient order selection algorithms for integer valued ARMA processes[J]. J. Time Series Anal, 2009(30):1-18.
    [14]Feike C. Drost, Ramon van den Akker, Bas J.M. werker. Efficient Estimation of Autoregression Parameters and Innovation Distributions for Semiparametric Integer-Valued AR (p) Models[J]. J.R. Statist. Soc. B, 2009(71):467-485.