噪声、跳跃与高频价格波动

    内容提要：高频数据中的噪声和价格跳跃使得波动的估计缺乏一致性，本文提出用门限预平均实现波动的方法估计同时存在市场微观结构噪声和价格跳跃时高频价格波动，该方法是资产价格实际波动的一致估计，并有最优的收敛速度。模拟发现，门限预平均实现波动和常用的高频波动估计方法相比，有更小的均方误差。中国证券市场的实证分析表明，门限预平均实现波动能减少波动预测误差，得到更为精确的风险管理价值。
关键词：噪声/跳跃/门限预平均实现波动作者简介：马丹，统计学博士，西南财经大学统计学院副教授，Email:madan@swufe.edu.cn（四川成都610071）；尹优平，经济学博士，研究员，北京大学光华管理学院博士后（北京100871）。
        
        一、引言
    正确估计金融资产价格波动对金融风险管理具有非常重要的意义，是长期以来理论界和实务界关心的焦点。随着金融统计方法的发展，用实时交易数据（也称为高频数据）估计资产收益波动成为研究的热点。“实现波动”（Andersen和Bollerslev，2000，2001，简称为RV）是一类主要的利用高频数据估计价格波动方法。当资产价格服从连续路径的It过程时，RV是波动的一致估计量。但是，高频数据通常会受到市场微观结构噪声和价格中的跳跃成分的“污染”。微观结构噪声和跳跃使RV是波动的有偏且不一致估计量，特别在采样频率非常高的时下，RV更主要地估计了噪声的波动而不是，资产价格的波动。
    针对“实现波动”的缺陷，许多学者提出了各种修正微观结构噪声或者价格跳跃的方法。修正微观结构噪声的方法可以分为稀疏抽样和预平均法两大类。稀疏抽样是通过降低抽样频率，减少微观结构噪声的影响，例如用五分钟、十分钟甚至更低频率的数据估计波动。稀疏抽样虽然降低了微观结构噪声，但采样频率的降低会损失有用信息。另一种方法是Jacod等（2009）提出的预平均法（Pre-Averaging），该方法是用连续函数对高频数据进行光滑处理，减少微观结构噪声的影响。预平均法包括了一大类平滑降噪的方法，例如，Zhang等（2005）提出的双尺度实现波动、Barndorff-Nielsen等（2006）提出的核光滑实现波动等都可以视作预平均法的特例。当资产价格只受到噪声的影响时，预平均法能够得到资产价格波动的稳健估计量，并有最优收敛速度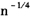①。然而，资产价格存在跳跃成分时，如果仍然利用预平均法估计积分波动，不但不能减少跳跃成分的影响，反而会出现增加跳跃点个数，使得估计的积分波动是有偏的。
    另外有些学者对资产价格存在跳跃时资产价格波动的估计问题进行了研究。Barndorff-Nielsen和Shephard（2004）提出的双幂次实现波动（记为BPV）是修正价格跳跃成分常用的方法。这种方法是利用相邻资产价格绝对值乘积的形式估计有跳跃时候的资产价格波动。Corsi等人（2009）指出，在有限样本下，如果某个时刻价格发生了跳跃，该时刻价格的绝对变化将增大，BPV会出现高估资产价格波动的偏误。他们提出用门限剔除价格跳跃，然后再用双幂次实现波动估计价格波动，即门限双幂次方法（记为TBPV）。模拟与实证研究表明TBPV能较好地估计价格变化中有跳跃成分时候的资产价格波动。Mancini（2011）在连续布朗运动模定理基础上提出了剔除价格跳跃的方法，并建议用门限的方法去掉跳跃，再用RV方法估计资产价格波动。以上方法在剔除价格跳跃时具有较好的性质，但当价格中存在微观结构噪声时，这些方法估计的价格波动仍然是有偏和不一致的。
    由于价格的跳跃破坏了价格服从连续随机过程的一系列假定，估计同时存在噪声和跳跃时的价格波动比较困难，因此大多文献是分开讨论噪声或者跳跃的影响，而同时考虑噪声和跳跃的文献较少。Fan和Wang（2007）提出了一种噪声和跳跃同时存在时波动估计方法，在资产价格序列满足Hlder连续条件假定下，利用线性小波识别和剔除跳跃上，再用双尺度实现波动方法估计价格波动。Fan和Wang（2007）的方法存在两个方面的问题：一是资产价格序列满足Hlder连续时才能使用该方法识别跳跃，在采样频率降低时，该条件难以成立；二是识别跳跃的小波估计统计性质不明确，限制了该方法的应用。Podolskij和Vetter（2009）提出了一种先消除噪声再剔除跳跃的方法，他们首先用预平均法对收益率序列进行降噪处理，然后用双幂次变差修正跳跃的影响，这种方法被称为修正的双幂次变差（MBV）。MBV是相邻序列取绝对值后的乘积，是噪声和跳跃同时存在时价格波动的一致估计。但是，MBV应用了双幂次实现波动的形式去掉跳跃，因此与双幂次实现波动一样，在有限样本下会高估资产价格波动。另外，Anderson等（2010）在将顺序估计量与预平均法结合提出了高频价格波动的一致估计，但在噪声比例比较大的情况下，该估计量的效果并不理想。
    综合现有研究，分别考虑噪声或者跳跃会使估计的资产波动是有偏和非一致的，而同时考虑噪声和跳跃的研究较少，这将是用高频数据进行风险管理的重要研究趋势。本文探讨存在跳跃时预平均修正的收益率性质，在此基础上将动态门限方法引入预平均框架，提出一种噪声和跳跃同时存在时，价格波动的估计方法。本文的贡献主要体现在以下三个方面：（1）在现有研究基础上，提出资产价格服从带有跳跃的噪声随机扩散过程时，新的高频波动估计方法——门限预平均实现波动。该方法避免了Podolskij和Vetter（2009）提出的修正双幂次变差在有限样本下高估价格波动的缺陷，并且是积分波动的一致估计，并能到最优收敛速度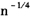；（2）探讨了利用预平均和门限方法结合使用时，预平均参数和门限参数的选择，修正了Corsi等（2010）提出的门限估计方法，避免了多次迭代运算和多个门限参数的主观设定；（3）利用模拟数据和实证数据对各类高频波动方法的效果进行了比较研究，特别是利用中国证券市场数据从波动预测、VaR计算方面比较了各类高频波动方法的估计效果，为使用中国证券市场高频交易数据估计价格波动提供方法选择。
    本文的研究框架如下。第二部分提出门限预平均实现波动并讨论其统计性质。第三部分通过模拟带有噪声和跳跃的常数随机波动模型和Heston-jump模型，比较门限预平均实现波动和五种高频波动估计方法效果，通过不同采样频率下各类方法的均方误差和平均误差分析，验证门限预平均实现波动能够分解出各种波动成分，具有较好的估计效果。第四部分利用中国证券市场高频数据进行实证分析，从波动预测方面比较了门限预平均实现波动和BPV的预测效果，在预测基础上，比较了门限预平均实现波动计算的风险价值和基于偏t分布GARCH的风险价值、RiskMetrics方法计算的风险价值。第五部分是本文的结论。
    二、门限预平均实现波动
    （一）门限预平均实现波动的提出
     
     
     
     
     
     
     
     
     
    三、模拟研究
    （一）主要的高频波动估计方法
    估计高频波动的方法可以分为三大类。第一类是有微观结构噪声时资产价格高频波动估计模型，这类方法的代表是Zhang等（2005）提出的双尺度实现波动（TSRV）和Jacod等（2009）提出的预平均实现波动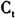（）。在没有跳跃时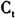，与TPRV是一致的，但存在跳跃时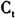，是波动的有偏估计，而TPRV仍然是一致估计。第二类是价格服从跳跃扩散过程的高频波动模型，这类方法的代表是Barndorff-Nielsen和Shephard（2004）提出的双幂次实现波动（BPV），该方法广泛应用于分解波动中的各种成分，而Crosi等（2010）证明了存在跳跃时BPV系统性地高估资产价格波动，并且进一步对该方法进行了修正，提出门限双幂次实现波动（TBPV），TBPV是有跳跃时资产价格的一致估计。第三类方法是同时存在微观结构噪声和价格跳跃时的高频价格波动模型，其典型的代表是Podolskij和Vetter（2009）提出的修正双幂次实现波动（MBV），该估计量是噪声和跳跃环境中，资产价格的一致估计量。
    我们将以上五种方法归纳为表1，并列出每种方法的具体计算形式。
     
    （二）模拟数据的产生过程
     
    其中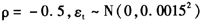，。模型参数为μ=[0.05/250，0.06/250，0.07/250]，κ=[5/250，6/250，7/250]，α=[0.05/250，0.06/250，0.07/250]，γ=[0.06/250，0.07/250，0.08/250]，这样产生三个不同的Heston-jump模型。由于中国证券交易所每日有4个小时的交易时间，目前价格的最高刷新频率为1秒/次。因此，最高采样频率为1秒。考虑到有限样本下估计量可能对样本大小很敏感，为比较采样频率对各估计方法的影响，我们模拟了分别以1分钟、30秒钟、10秒钟、5秒钟、2秒钟和1秒钟的为采样间隔的数据，对应的样本容量分别为240、480、1440、2880、7200和14400。每个样本容量的数据分别进行1000次模拟计算。
    （三）模拟结果的分析
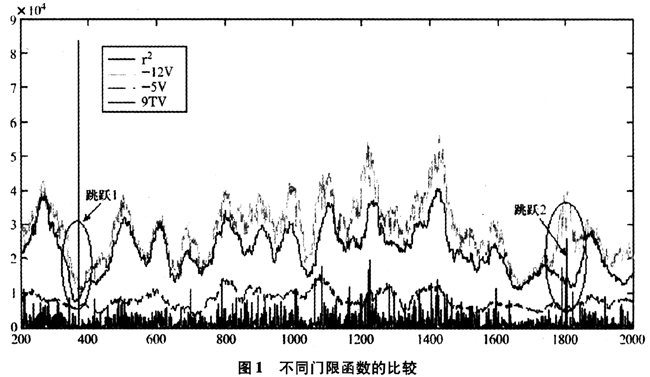
    在估计TPRV和MBV时，需要计算参数K的取值。在模拟时，分别计算了K取1到50整数时的均方误差（MSE），并以最小均方误时的K作为最后取值。图2是不同样本容量下TPRV估计量的对数均方误差情况。从图中可见，样本容量越小最优K值越小。当样本容量为240时最优K约为3，当样本容量为480时，最优K约为4，样本量为1440时，最优K为7，当样本量为14400时，最优K为26。
     
     
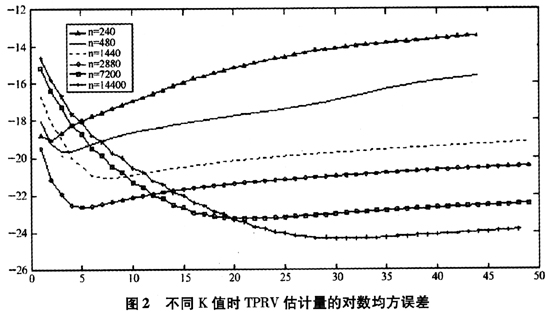
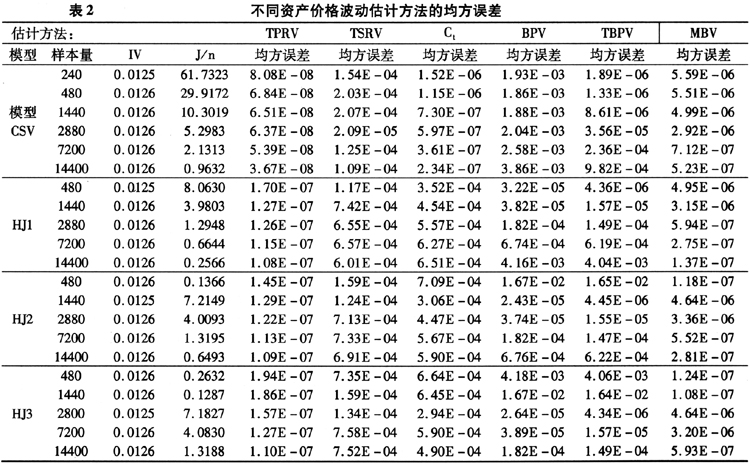
    表2给出了各种方法估计的资产价格波动均方误差。从均方误差来看，四个模型模拟数据均反映出TPRV模型有较小的均方误差，特别是CSV模型中，TPRV的均方误差非常小。从样本容量来看，在7200以上样本容量时，MBV的均方误差也比较小，但是TPRV在较小样本小的误差比MBV小的多。进一步可以发现，随着取样间隔的增加，高频数据中的微观结构噪声增多，跳跃和噪声比（J/n）下降。跳跃和噪声比很大和很小时，TPRV方法仍然得到最小的均方误差。TPRV对样本容量并不是非常敏感，这点在实际应用时很重要。中国证券市场流动性高的股票每日大约也只有2000笔交易，而中等流动性股票每日只有1000笔交易左右，还有许多流动性较差的股票每日只有200笔左右的交易。因此较小样本容量时估计量是否有稳定的表现，对于实践中正确估计资产价格波动非常重要。TSRV方法在跳跃和噪声比很小，即跳跃成分很小时得到的均方误差更小，BPV方法则在跳跃和噪声比很大时得到的均方误差更小，这说明这两种方法分别适用于仅有噪声或者仅有跳跃时资产价格波动的估计。
     
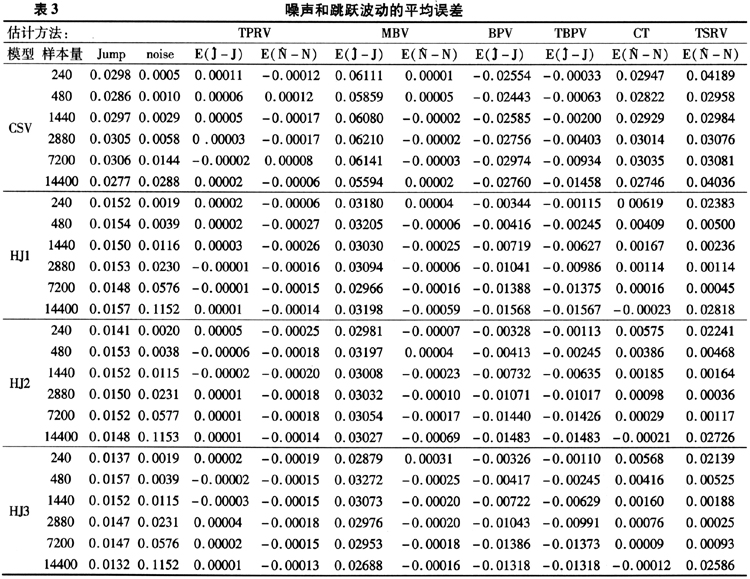
    表3给出了用六种方法估计的噪声和跳跃波动的平均误差。其中TPRV和MBV能够同时估计噪声和跳跃的波动，而BPV和TBPV只能估计跳跃的波动，Ct和TSRV方法只能给出噪声波动的估计。从六种方法估计结果来看，TPRV方法得到的绝对平均误差较小，MBV估计的结果并不理想。BPV、TBPV的资产价格波动中可能存在跳跃，因此剩下的跳跃估计误差较大。而CT和TSRV估计的噪声方差可能包含了跳跃的方差，有明显的高估。
    TPRV方法和MBV方法都同时能够估计资产价格波动、跳跃波动和噪声波动，从模拟结果来看，TPRV效果更好，特别在小样本下估计效果更理想。由于估计参数K随着样本量减少而减少，在小样本下K值较小。MBV是通过采用间隔为K的数据来避免跳跃的连续影响，但是当K值很小时，跳跃的连续影响可能持续到K期以后，因此MBV方法的效果并不理想。
    四、中国证券市场的实证分析与比较
    （一）资产价格波动预测效果的比较
    国内一些学者（如马丹和尹优平，2007；邵锡栋和殷炼乾，2008）对中国证券市场高频波动进行了实证研究，但大部分都只讨论了跳跃或者噪声情况下的波动问题，特别是用BPV方法估计有跳跃时的高频波动。我们选用中国石化2005年1月2日到2009年3月31日的高频数据分别用BPV和TPRV这两种方法估计高频价格波动，并分解出跳跃等波动成分，用HAR-RV-CJ模型对二者的预测效果进行比较。
    考虑到采样频率对估计结果存在影响，我们采用了分笔交易数据、15秒钟、30秒钟、1分钟和5分钟的分时交易数据，数据来源于CSMAR数据库。为了检验门限预平均方法的估计效果，我们将整个样本区划分为估计区和预测区，用估计的跳跃波动和连续成分波动对实现波动进行预测。2005年1月2日到2008年11月14日，共计900个交易日的数据用于估计资产价格波动，2008年11月15日到2009年3月31日共计90天作为预测窗口。分别利用TPRV方法和BPV方法得到资产价格波动、噪声引起的波动和跳跃引起的波动如表4所示。
    从估计结果来看，随着采样间隔的增加，实现波动逐渐降低。双幂次变差BPV的估计结果对采样频率非常敏感，分比交易数据的平均交易间隔是5秒钟，此时的噪声波动最大，而BPV高达0.0021，非常接近实现波动，这是由于BPV统计量并没有考虑微观结构噪声。随着采样频率的降低，噪声波动成分减少，BPV与TPRV估计结果趋近一致。用TPRV估计的资产价格波动对采样频率的变动敏感性已有所降低。跳跃引起的波动约占实现波动的2.01%—12.56%，这个结果与Fan和Wang（2007）的研究基本一致。噪声引起的波动随着采样频率的减少而递减，在5分钟数据中，噪声的比重仅占12.22%。在不同采样频率下，BPV估计的资产价格波动始终高于TPRV，这说明忽略微观结构噪声将导致资产价格波动的高估。
    为比较不同估计方法的效果，我们采用Crosi（2004）提出用HAR-RV-CJ模型对预测窗口期的实现波动RV进行预测。模型的形式为：
     
     
     
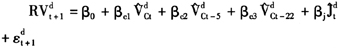
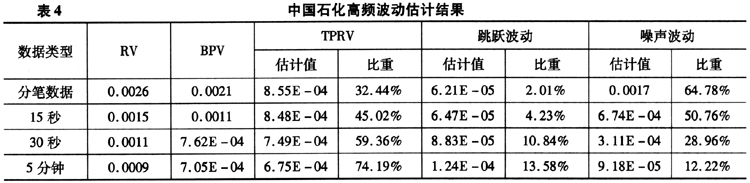
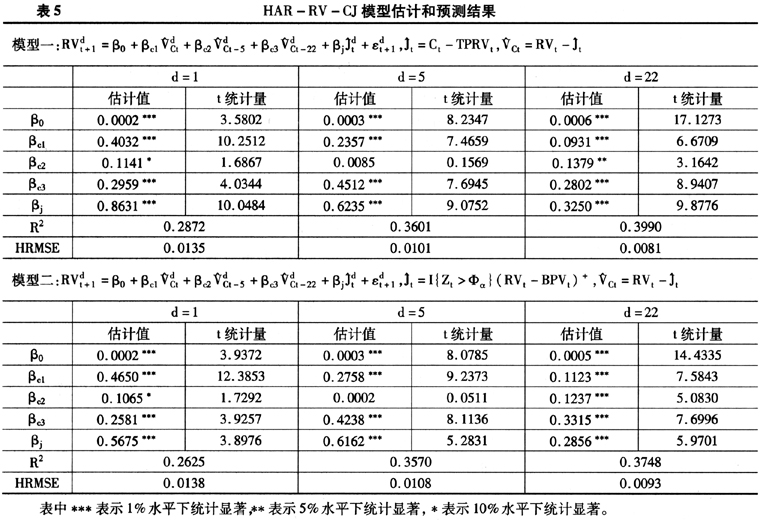
    表5给出了用两类HAR-RV-CJ模型的估计结果。从样本内拟合效果来看，随着数据频率的降低，两模型的拟合效果均有所提高。BPV和TPRV方法得当的跳跃成分对RV均具有显著的影响，但模型一中的跳跃成分显著性水平更高，Corsi等（2009）指出门限方法能够显著提高跳跃成分在HAR类模型中的显著性，与我们的研究结论一致。另外，无论是1天、1周或1月的RV模型来看，模型一的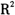都大于模型二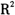，说明门限预平均方法分解的连续成分波动和跳跃成分波动对RV具有更好的解释力。
    我们利用前900个交易日数据对后90个交易日的RV进行预测，并比较了两种模型的预测效果。在比较模型的预测效果时，选择异方差调整均方误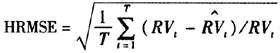作为比较标准。从两类模型的预测效果来看，随着数据频率的降低，两类模型的预测效果均有所提高。模型一的异方差调整均方误更小，预测效果比模型二更为理想。
    （二）基于门限实现波动的风险价值
    HAR-RV-CJ模型得到波动预测，进而可以计算风险价值（VaR）。在计算VaR时，通常分别计算多头和空头头寸的VaR值，其具体计算方法是：
     
     
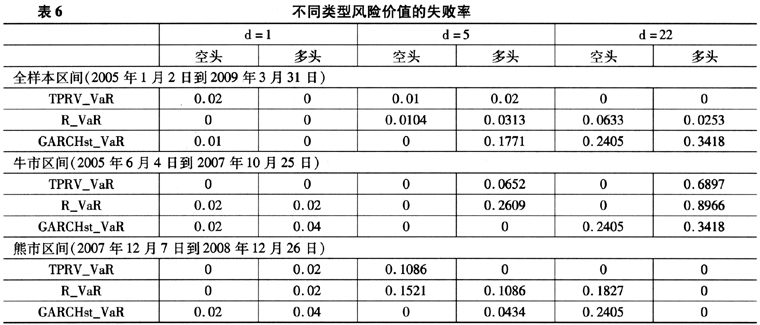
    2005年1月2日到2009年3月31日，中国股市经历了牛市和熊市，不同市场行情中，各种风险管理方法表现大相径庭，因此我们计算了全样本区间和牛市、熊市下的VaR值。在计算时，采用滚动样本的方法以避免异常值对计算结果的影响，并分别计算了1天、1周和1月的风险价值。表6给出了在不同时间段，基于门限实现波动的风险价值（TPRV_VaR），基于偏t分布GARCH的风险价值（GATCHst_VaR）和RiskMetrics方法计算的风险价值（R_VaR）计算效果。
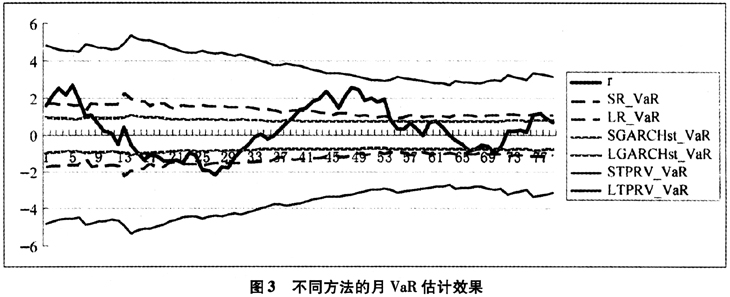
    从表6可见，与常用的风险价值计算方法相比，TPRV_VaR的失败率比较低，特别是在全样本区间，TPRV_VaR的效果明显比其他方法更好。图3绘制了全样本区间的三种估计方法得到的月VaR（d=22）和实际月收益。
    从图3可以看出，月收益率均有超出GARCHst_VaR和R_VaR的情况，这两种方法得到风险价值偏低，TPRV_VaR能够较好预测可能的损失。导致这种情况的原因在于，TPRV_VaR是利用了日内信息计算的，而且在TPRV_VaR预测时，单独考虑了价格跳跃因素的影响，特别在价格变化幅度加大时，对预测未来波动具有重要意义。
    从不同时间区间的计算结果来看，牛市的风险价值估计效果比熊市差，特别是在熊市中，TPRV_VaR的长期风险管理（d=22）效果显著优于其他方法，这是由于在TPRV_VaR预测波动时，利用了HAR-RV-CJ模型，这实际上是一种混合频率模型，对波动预测考虑了短期、中期和长期因素，而GARCH仅用短期（通常是1天）信息进行预测，RiskMetrics虽然可以利用多天信息，但当平滑窗口确定时，RiskMetrics也是固定频率模型，因此在各时间区间，TPRV_VaR具有较好的长期风险管理效果。此外，在牛市中，三种方法计算的VaR均表现不佳，特别是月VaR的失败率较高，这是由于我们在计算时有意识的选取了牛熊市转折期作为预测起点，由于三种模型均不能考虑转折期的影响，导致月VaR的预测结果不理想，加入markov机制转换等反映数据阶段变化的因素可能会提高VaR预测的准确性。
     
     
    五、结论
    本文提出用门限预平均实现波动估计同时存在微观结构噪声和价格跳跃时的资产价格波动，通过模拟与实证分析得到以下结论：
    1.门限预平均实现波动是同时存在微观结构噪声和价格跳跃时的资产价格波动的一致估计，该方法不仅能够估计出资产价格变化，并能分解资产价格波动因素，例如噪声引起的波动和跳跃波动等。与现有的门限预平均类方法相比，门限预平均方法在两方面有所改进，一是修正了估计，得到积分波动的一致估计，避免了MBV估计在有限样本下高估积分波动的问题，并通过模拟验证了TPRV在小样本下估计效果明显优于MBV；二是改进了Corsi提出的门限函数设定方法，提出的门限函数能够避免门限值设定的主观性，通过一次运算即可得到较好的结果，无须多次迭代运算。
    2.利用中国石化分笔数据、15秒、30秒和5分钟交易数据建立了HAR-RV-CJ模型，并对1天、1周和1月的波动进行预测。实证结果表明，门限预平均方法能够更好的拟合HAR-RV-CJ模型，与常用的BPV方法估计的HAR-RV-CJ相比较，具有更小的预测误差。
    3.用门限预平均实现波动分解出资产价格波动因素，能够计算风险价值，该方法计算的风险价值与常用的GARCH和RiskMetrics相比，能利用日内、短期、中期和长期价格信息，因此预测VaR的准确率更高。但是值得指出的是，用HAR-RV-CJ模型预测波动并没有考虑状态转换等因素，在行情转折期进行风险管理时应该在HAR-RV-CJ模型中加入Markov机制转换等方法以提高预测效果。
    感谢匿名评审人的意见。
    注释：
     
    ③由于篇幅限制，略去了对门限预平均统计量性质的数理证明，感兴趣的读者可以向作者索要。
    ④Patton（2010）指出当波动估计方法是有偏误的时候，MSE仍然是比较各类波动模型的稳健损失函数。
     
参考文献：
        [1]邵锡栋、殷炼乾，2008，《基于实现极差和实现波动率的中国金融市场风险测度研究》，《金融研究》第6期，第109～121页。
    [2]马丹、尹优平，2007，《交易间隔、波动性和微观市场结构——对中国证券市场交易间隔信息传导的实证分析》，《金融研究》第7期.第165～174页。
    [3]Andersen, T. G., Bollerslev, T., Diebold, F., et al., 2000, "Exchange rate returns standardized by realize volatility are(Nearly)Gaussian," Multinational Finance Journal, 3(4), pp. 159～179.
    [4]Andersen, T. G., Dobrislav Dobrev, Ernst Schaumburg Dobrislav Dobrev, Ernst Schanmburg, 2010, "Jump-robust volatility estimation using nearest neighbor truncation," NBER Working Paper No. 15533. http://www.nber.org/papers/w15533.pdf?new_window=1.
    [5]Barndorff-Nielsen, O. E., Shephard, N., 2004, "Power and bipower variation with stochastic volatility and jumps," Journal of Financial Econometrics, 2(1), pp. 1～48.
    [6]Barndorff-Nielsen, O. E., Barndorff-Nielsen, O. E., P. R. Hansen, A. Lunde, and N. Shephard ,2006, "Designing realised kernels to measure the ex-post variation of equity prices in the presence of noise," Econometrica , 76(6), pp. 1481～1536.
    [7]C Mancini and Roberto Ren, 2011, "Threshold estimation of Markov models with jumps and interest rate modeling realized volatility," Journal of Econometrics, 160(1), pp. 77～92.
    [8]Fan, J. and Wang, Y, 2007, "Multi-scale jump and volatility analysis for high-frequency financial data," Journal of American Statistical Association,(102), pp. 1349～1362.
    [9]Fulvio Corsi, Davide Pirino and Roberto Ren, 2010, "Threshold bipower variation and the impact of jumps on volatility forecasting," Journal of Econometrics, 159(2), pp. 276～288.
    [10]Jacod, J., Li, Y., Mykland, P. A., Podolskij, M., et al. 2009, "Microstructure noise in the continuous case: The pre-averaging approach," Stochastic Processes and Their Applications,119(7), pp. 2249～2276.
    [12]K. Christensen, R. Oomen and M. Podolskij, 2011, "Realised quantile-based estimation of the integrated variance," Journal of Econometrics, 159(1), pp. 74～98.
    [13]Mark Podolskij and Mathias Vetter, 2009, "Bipower type estimation in the noisy diffusion setting," Stochastic Processes and Their Applications , 119(9), pp. 2803～2831.
    [14]Zhang, L., Mykland, P. A., Ait-Sahalia, Y., 2005, "A tale of two time scales: Determining integrated volatility with noisy high-frequency data," Journal of the American Statistical Association,(100), pp. 1394～1411.