股票市场微观结构噪声、跳跃、流动性关系分析

    内容提要：在金融高频数据研究领域，学者们关于不同类型风险的内在关系并未深入探讨。从高频数据角度，本文首次对市场微观结构噪声、波动率跳跃之间的关系进行了理论分析。估计出微观结构噪声方差，通过构造新的跳跃分离方法，分离出波动中跳跃成分，给出流动性度量指标，并以上证综合指数为例，对微观结构噪声、跳跃、流动性三者关系进行实证分析。结果表明噪声越大指数发生跳跃的可能性越高；流动性越强指数的噪声越小，并且发生跳跃的可能性越低，并对此现象给出相应的解释。
    关键词：微观结构噪声/跳跃/流动性
    作者简介：唐勇（1970-），男，汉族，江苏洪泽人，福州大学管理学院副教授，博士，研究方向：金融计量、风险管理；寇贵明，福州大学管理学院（福建福州350002）。 
        1引言
    对微观结构的研究一直是金融市场研究的重要议题之一。金融高频数据的广泛使用为研究金融市场微观结构提供了新的途径和方法。当前，国内外关于金融高频数据的研究主要集中在波动率的研究上，其主要有两大研究领域：一是关于微观结构噪声性质的研究以及基于微观结构噪声（后文均简称噪声）给出的噪声稳健型积分波动估计量的研究：如Zhang等（2005）[1]提出的双尺度已实现波动（TSRV），Zhang（2006）[2]提出的多尺度已实现波动（MSRV），Barndorff-Nielsen等（2009）[3]提出的已实现核估计以及Jacod等（2009）[4]提出的前项平均（Pre-Average）方法等；二是基于伊藤半鞅过程，研究波动率的跳跃行为。这一领域的研究主要分为两个方面：一方面主要是关于跳跃稳健型积分波动的估计，如Barndorff-Nielsen与Shephard（2006）[5]提出的双幂次变差（BPV），Mancini（2009）[6]提出的门限双幂次变差（TRV）与门限多幂次变差（TMRV），Andersen等（2010）[7]提出的最小已实现波动（MinRV）与中位数已实现波动（MedRV），以及Christensen等（2010）[8]提出的基于分位数的已实现波动（QRV）等；另一方面则主要是对跳跃检测统计量的研究，如Barndorff-Nielsen与Shephard（2006）[5]的BN-S检验统计量，Jiang与Oomen（2008）[9]的J-0检验统计量，Lee与Mykland（2008）[10]的L-M统计量，以及Ait-Sahalia与Jacod（2009）[11]的A-J检验统计量等。
    目前研究基本放在波动率的估计上，对于利用金融高频数据研究噪声、跳跃与流动性关系的文献还相对较少。Ait-Sahalia与Yu（2009）[12]研究表明流动性越大的股票所包含的噪声越小；Andersen等（2007）[13]、Lahaye等（2010）[14]在分析跳跃产生的原因及跳跃与宏观经济信息发布关系时，认为一般波动率的跳跃发生在宏观信息的发布之后，但是没有说明宏观信息通过什么方式导致跳跃；Jiang等（2010）[15]则从普遍认为导致噪声发生的宏观信息的发布出发，认为宏观信息的公布使得市场产生流动性冲击（liquidity shocks），从而使资产价格的波动发生跳跃行为；Giot等（2010）[16]考虑了已实现波动、跳跃波动与成交量的关系，并从交易的活跃性等流动性指标分析价量关系，得出跳跃与成交量的关系并非显著为正。
    从现有的研究上看，关于微观结构噪声、跳跃、流动性之间的关系还没有系统的研究与分析。分析三者之间的关系，能够使我们更为准确地对波动率进行度量，提高风险度量准确性，并且能够分清市场风险类型，探究噪声行为、金融市场异常风险、流动性风险之间的关系，从而更为有力的对不同类型的风险进行防范与管理。鉴于此，本文尝试从理论和实证上对此问题进行探讨，以便理清三者之间的关系。
    2理论分析
    2.1理论基础
     
    而当资产价格过程存在着有限跳跃时，在给定的过滤概率空间下，资产价格过程服从伊藤半鞅过程.具有如下的形式：
     
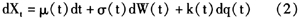
    其中μ（t）是一个连续的、局部有限漂移函数，σ（t）是一个适应的左极限存在、右连续的随机波动过程（adapted càdlàg stochastic volatility process），W（t）是一个标准布朗运动，q（t）是具有一定强度的计数过程，k（t）反映了价格过程的跳跃大小。
    运用金融高频数据度量资产收益的波动率，一般是通过二次变差（quadratic variation，QV）过程来实现的[13]。式（2）的二次变差过程为：
     
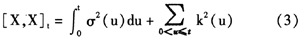
    因此，资产收益的波动率可分为两部分：连续样本路径方差与不连续的跳跃。连续样本路径方差可以被看成是正常事件所引起的资产价格平滑的波动，跳跃则可看成是极端事件所导致资产价格的跳跃波动。将波动率分成这两类方差能够使我们更好地对波动率进行度量，分析波动率的性质，并且依据这两种不同性质的风险可以对资产进行重新定价。
    由二次变差理论可知，当抽样时间间隔无限小时，已实现波动（RV）依概率收敛于二次变差增量过程[13]，形式如下：
     
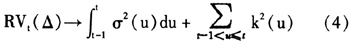
    显然，RV的估计包含了积分波动与跳跃成分。关于两类波动率方差的划分上，现有的学者从连续样本路径的方差着手，更注重分析资产价格的积分波动，即在一定时期内金融资产价格变动的度量。积分波动形式为：
     
    其中t的选择取决于研究的目的。如果研究关注日（周）波动率，那么t就代表着一天（周），得到也是一天（周）的波动率。
    由式（4）与式（5）相减得到的差，就是波动率的跳跃成分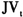，即为：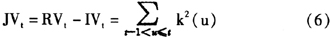
     
    因此，理论上在无噪声情况下，可以通过式（6）得到跳跃成分，分析市场的不平滑的跳跃波动以及跳跃的相关性质。
    2.2跳跃与噪声关系讨论
    现实金融市场是一个有摩擦的市场。由于闭市效应、买卖的局限性、价格变动的离散性、不同步交易等因素导致我们所观察到的价格过程是一个包含噪声的过程。特别是在高频数据环境下，价格包含着信息丰富的市场微观结构噪声。一般所观察到的对数价格过程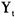包含了不能观察到的对数有效价格过程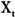和噪声成分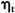，相应的收益率表示为：
     
    因此，从上述式子中可以看出，不仅二次变差的估计受到噪声的影响，已实现波动、积分波动与波动率跳跃的估计同样受到噪声的影响。
     
    （记：噪声方差为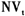）。因此，由（11）式可以看出跳跃与噪声之间会相互影响。在度量跳跃与波动时，过低或过高估计噪声都不能正确度量市场的波动率跳跃，但是（11）式不能确定噪声与跳跃之间的关系。因此，下面本文选择适当方法，来探讨两者之间的关系以及它们与流动性之间的关系。
    3估计方法与统计量选择
    现有的研究提出了许多噪声与跳跃的分离方法，每种方法建立的假设前提都不太相同。对跳跃估计时要基于两方面考虑：一方面要选择一个对于噪声与跳跃都稳健的积分波动估计量，另一方面则必须选择跳跃检验统计量来对是否发生跳跃进行检验。同样的，流动性的度量指标有很多，本文对流动性指标的选取是基于我国股票市场现实交易机制下进行选择。
    3.1噪声方差估计方法的选择
    许多学者对噪声分析时，都是建立在式（10）的假设之上，选择信噪比方法来估计噪声方差。本文选择常用的Bandi与Russell（2006）[17]方法来估计噪声方差，此方法利用不同抽样频率下的抽样矩得到了噪声方差的一致估计量。
    3.2积分波动估计方法的选择
    由于高频数据当中不仅存在着跳跃、噪声，有时还存在着异常值。在几种常见的稳健型积分波动估计量当中，Christensen等（2010）[8]提出了QRV，并进行改进得到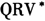作为积分波动的估计量，其对噪声、跳跃以及异常值都是稳健的，并且对于积分波动拥有最快的收敛速度。因此，本文选择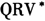作为积分波动的一致估计量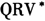，的定义如下：
     
    3.3跳跃检验统计量的选择
    在几种跳跃检验统计量中，Ait-Sahalia与Jacod（2009）[11]所提出的A-J检验统计量所需要的假设较少，并且A-J检验统计量针对有限活动的跳跃与无限活动跳跃都有效，这又有利于在区分度量误差与较小跳跃的基础上，能够比较准确的甄别跳跃行为。因此，本文选择A-J检验统计量来对是否发生跳跃行为进行检验。
    A-J跳跃检验统计量是通过两个不同抽样频率幂变差之比来判别波动率是否发生跳跃行为，令：
     
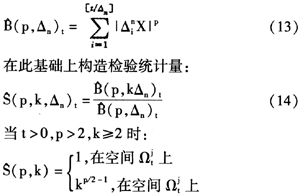
    因此可以通过判断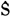（p，k）接近于1来进行分析是否发生跳跃行为。但是在实际的计算当中，较难判断一个数值是否接近1。因此，Ait-Sahalia与Jacod（2009）[11]提出了跳跃检验统计量判别的临界值，当原假设为没有跳跃行为时，拒绝区域为：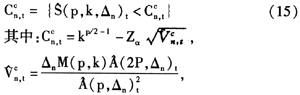
     
    则根据Andersen等（2007）[13]，在考虑噪声的情况下构建新的跳跃波动，其可以表示为：
     
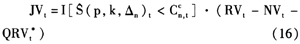
    其中I[·]代表示性函数。
    3.4我国股票市场流动性度量指标选择
    市场的流动性是一个较为抽象的概念，一般是通过一些指标来进行刻画。我国股票市场是一个订单驱动市场，与美国等的报价驱动市场存在着一定的区别，因此在构造流动性指标时也存在着一定的差异。本文参照Ait-Sahalia与Yu（2009）[12]的方法，利用高、低频数据选取国内学者[18]常用的流动性度量指标对股票市场的流动性进行刻画。
    日内流动性度量指标向量H为：
    H=（LTS，LT）
    其中：LTS为对数平均每笔交易量，LT为对数每日成交笔数。
    日间流动性度量指标向量D为：
    D=（LV，LOGP，TO，ILLIQ）
    其中：LV为对数日成交量，LOGP为对数收盘价，TO为每日换手率，ILLIQ为Amihud（2005）[19]提出的非流动性指标，其具体计算公式为：
    ILLIQ=|R|/（P*VOL）（17）
    其中：R为每日收益率，P为收盘价，VOL为每日成交量，则总的流动性度量指标为：
     
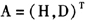
    4实证分析
    4.1数据选择与处理
    本文选取2007年1月4日至2010年3月1日上证综合指数分笔数据、1分钟数据，这些数据包含换手率、成交量、成交额等指标，除掉不完整的交易数据之后，共775个交易日。
    4.2噪声、跳跃估计
    由Bandi与Russell（2006）[17]所提出的噪声方差一致估计量，估计出噪声方差。
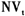    进行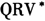估计时，基于式（10）假设的前提下，在消除噪声的基础上，采用子抽样方法来代替分块方法得到估计量。其中，需要确定几个参数：子抽样K的选择，m的选择以及分位数λ的选择。在此与Christensen等（2010）[8]的选择一样，选择λ=｛0.80，0.85，0.90，0.95｝。而由于利用的是1分钟的高频数据，因此选择m=40。一般情况下，K值一般在0-25之间，而本文所采用的数据是1分钟抽样频率的数据，每天只有240个交易数据，因此采用枚举法来对2-6之间的K进行选择，并根据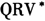的对数均方误差（logMSE）的大小来确定K值。本文所用软件为Matlab7.0，其中编程代码源自Podolskij（2009），并在其基础上进行相应修改。计算不同K值下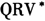的logMSE，如表1所示。从表1可以看出当K=6时，计算出的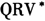的logMSE值达到最小，因此选择K=6来对数据进行前平均处理，其中所使用的核函数为h（x）=min（x，1-x）。通过相应计算得到RV、NV和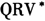序列，并由式（11）可以得出JV序列。
    RV、NV、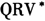、JV序列的统计特征如表2所示。从以上四种方差的统计特征上看，四个方差都呈现出尖峰的特征，LB检验统计量都显示出四个序列的分布都非正态分布。
     
     
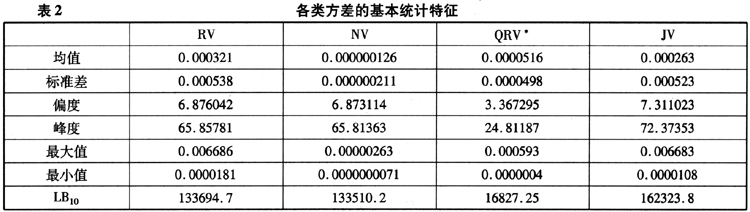
    通过Eviews5.0软件得出四种方差序列的图形，如图1所示。从图形当中可以看出，已实现波动、噪声方差与跳跃序列图极为相似。特别是噪声方差与跳跃序列图的相似性，需要进一步分析二者之间的关系。
     
    4.3噪声与跳跃的关系分析
    由于不同跳跃检验统计量检验出的跳跃有所差异，为了避免跳跃检验统计量的因素影响跳跃与噪声关系的分析，所以分别对检验前与检验后的跳跃与噪声的关系进行分析。
    4.3.1检验前的跳跃与噪声的关系分析。
    在忽略度量误差的基础上，分析由（11）式得出的跳跃方差与噪声方差之间的关系。检验两个序列的平稳性，得到表3。
     
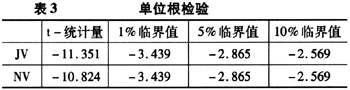
    从检验的结果上看，在1%、5%、10%的置信水平下，跳跃方差序列与噪声方差序列都是平稳的。由跳跃方差的自相关检验可以得到检验前的跳跃方差存在一阶自相关，同时为了考虑前一期噪声对于当期的影响，因此进行如（18）式的线性回归，其结果如表4所示。
     
     
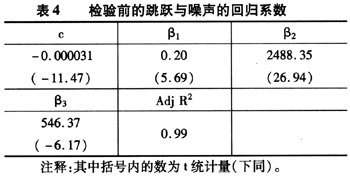
    从回归的结果上看，回归系数较为显著。跳跃方差序列与噪声方差序列之间存在着明显的正相关关系。为了进一步确认两者之间的关系，将两个序列进行格兰杰因果关系检验。由AIC与SC准则确定滞后阶数为3，则两者之间的格兰杰因果关系，检验结果见表5。
     
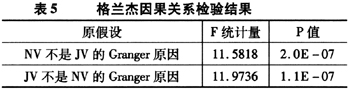
    从表5格兰杰因果检验的伴随概率可以拒绝原假设，即认为噪声与跳跃之间互为因果关系。由于上面所得到的跳跃是在假设不存在度量误差的基础上得到的，但是度量出来的较小的跳跃可以视为连续抽样样本上的一部分，或者是由于度量上的误差所引起的，因此下面本文选择跳跃检验统计量来甄别出跳跃序列。
    4.3.2检验后的跳跃与噪声的关系分析。
     
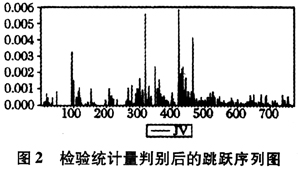
    在引入临界值后，发现α=0.05时，拒绝率为0.26。由式（16）得到检验后的跳跃，如图2所示。与图1相比，从图2中可以看出，上证指数发生连续跳跃的情形较小。通过自相关检验，发现检验后的跳跃序列本身不存在自相关性。
     
    用A-J方法进行跳跃检验后，即根据（16）式得到跳跃方差序列。进行平稳性检验后发现，检验后的跳跃方差与噪声方差仍都是平稳的，并将二者序列进行回归。由于检验后的跳跃方差序列不存在一阶自相关，因此选择（19）式的回归形式，得到表6的回归结果。
     
     
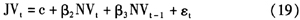
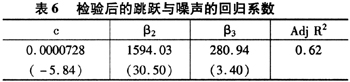
    从回归系数上看，回归系数依然显著。因此，跳跃方差序列与噪声方差序列之间存在着正相关关系。同样将两个序列进行格兰杰因果关系检验，发现二者之间仍互为格兰杰因果关系，见表7。
     
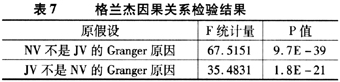
    因此，由上面的分析可以看出：无论是检验前的跳跃序列还是检验后的跳跃序列，它们与噪声方差序列的关系显著为正，即指数的噪声越大更易于发生波动率的跳跃，并且它们都与噪声互为因果关系。
    4.4跳跃与流动性的回归分析
    通过计算得到流动性度量指标的数据之后，将上面得出跳跃方差序列（包含检验前与检验后的序列）与流动性指标进行线性回归。考虑到引起跳跃的流动性因素对跳跃的影响是短暂的，因此本文仅考虑了前一期的流动性与当期流动性对于跳跃的影响。由前文知，检验前的跳跃方差序列存在着一阶自相关性，而检验后的跳跃方差序列不存在自相关性，因此分别利用式（20）和式（21）进行回归。
     
     
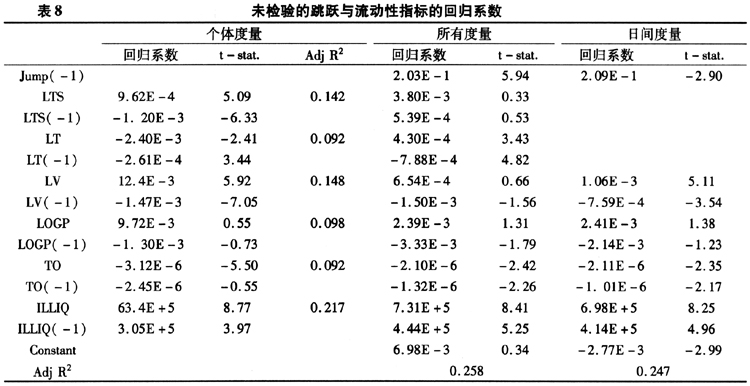
    为了比较高低频数据得到的流动性指标对于跳跃的不同程度的影响，本文将检验前与检验后的跳跃方差序列与向量A中的流动性度量指标进行多元线性回归，分别得到表8与表9中的“所有度量”部分的系数；将跳跃方差序列与向量D中的流动性度量指标进行多元线性回归得到“日间度量”部分的回归系数。其中：未检验跳跃方差序列与流动性指标的回归方程为式（22）与式（23），检验后的跳跃方差序列与流动性指标的回归方程为式（24）与式（25）。
     
     
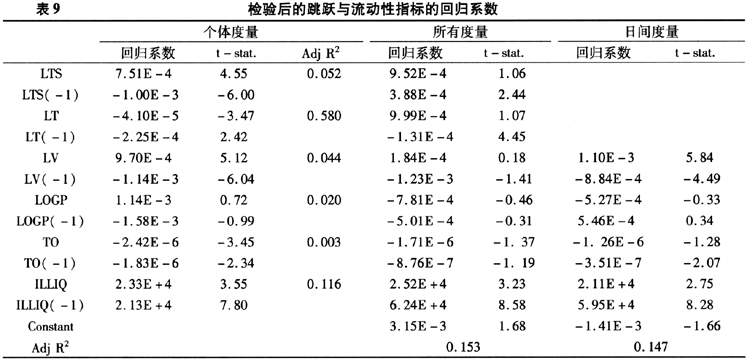
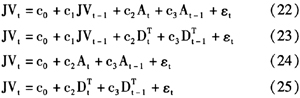
    由表格8与表格9的回归结果可以得到以下结论：（1）前一期与当期的非流动性指标与跳跃之间呈现出正相关关系，而非流动性指标越大反映出市场的流动性越弱，这种正相关体现出流动性与跳跃之间为负相关关系；（2）成交笔数与换手率反映了市场的交易活跃程度，所有的系数均为负数，也就是说流动性越大则发生跳跃的可能性也就越小；（3）前一期与当期的对数平均每笔交易规模、对数成交量、对数收盘价三个指标对跳跃的影响有所差异。对数平均每笔交易规模、对数成交量反映的是成交的规模的大小。前一期的交易规模的放大可能使得当期的动能不足，反而使得当期股市发生跳跃的可能性降低，因此前一期的对数平均每笔交易规模、对数成交量与当期跳跃的回归系数为负。而当期对数平均每笔交易规模、对数成交量与跳跃的回归系数为正则可以解释为交易规模的突然放大引起波动率发生跳跃行为；（4）多元线性回归的回归结果显示，多元回归的系数与一元线性回归的结构差别不大。从拟合效果上看，考虑了由高频数据获取的日内指标的拟合优度更高，因此考虑日内的流动性度量指标更能充分地分析流动性与跳跃之间的关系。
    总体上看，无论是一元线性回归还是多元线性回归，回归系数显示流动性与跳跃之间呈现出的是一种负相关关系，即流动性较高的时候市场发生异常风险的可能性越小。
    4.5噪声与流动性的回归分析
    前文的回归结果显示跳跃与噪声之间关系为正相关，跳跃与流动性之间的关系为负相关，可以猜测噪声与流动性之间的关系为负相关。为了证实两者之间的关系，同样将噪声方差序列与流动性度量指标进行回归。与文献[12]的回归不同，此处考虑了前一期的噪声和流动性对于当期噪声的影响，回归方程如下（结果见表10）：
     
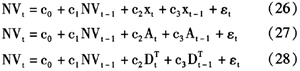
    表10中回归系数的符号与表8、表9的回归系数符号较为相似。由于噪声的值较小，因此回归的系数也相对较小。从表10回归的系数看，可以得出以下结论：（1）在个体度量当中，噪声与对数成交笔数、对数收盘价、换手率等指标的回归系数不管在是在当期还是在上期都显著为负；对数平均每笔成交量、对数成交量对噪声的影响在前一期与当期有所差别。当期噪声与前一期的对数平均每笔成交量、对数成交量关系为负，而与当期为正；非流动性指标与噪声的回归系数为正，显示出流动性越强，则噪声越弱。（2）从所有度量的回归结果上看，当将所有的流动性度量指标与噪声进行回归时，只有前一期的对数平均每笔成交量发生变化，其他系数均未改变符号。（3）调整的显示，考虑日内与日间的流动性度量指标的回归较只考虑日间流动性度量指标的回归效果有所提高。
     
    总体上看，几个流动性度量指标与噪声之间的关系为负，因此可以得出噪声与流动性之间的关系为负，即指数流动性越强噪声越小，该结论与文献[12]得出的结论一致。
    4.6原因分析
    与国外成熟市场相比，我国股票市场还不成熟，研究表明我国股票市场是弱式有效的。从数量上看，机构投资者占少数，数量众多而分散的中小投资者占据主导地位。由于信息披露等监管制度尚不规范，一些大投资机构往往是知情交易者（informed trader），他们能掌握足够的特定的公开信息，甚至是私有信息，并有可能进行内部交易，严重损害了中小投资者的利益。这些中小投资者也往往是噪音交易者（noise trader），他们由于时间、精力等方面的限制，无法及时获得信息并做相关处理，所以存在信息的严重不对称。中小投资者往往采用正反馈交易策略，倾向于进行“追涨杀跌”，因此，中小投资者或者噪音交易者往往也会成为非理性交易者[20]。在这种背景下，中国股市表现出特有的特征。
    前文基于高频数据波动度量方法，对上证综指噪声、跳跃与流动性关系做了实证分析，为何上海股市中这些金融变量会呈现这样的关系，迄今鲜有给出合理的解释。为此，此处尝试给出一些分析。一方面，就噪声与跳跃而言，表面上来看噪声是由于买卖价差、交易离散程度等价格信息原因引起的，实际上是由特定的相关信息引起的。目前跳跃形成机理研究结论远未达到一致，但是特定的相关信息会造成跳跃的发生，这一点是一致的[21]。这些特定的信息首先被一些知情交易者所捕获，在股票市场表现为往往是股票价格发生跳跃，这就必然导致买卖价差加大、交易离散程度提高，导致了噪声程度提高。同时，市场上的知情交易者远非只有一个，有时他们为了各自的利益，可能存在博弈过程。一些知情交易者为了自己利益，有时利用掌握的特定信息改变价格信息（例如加大买卖价差等），这样会导致噪声程度提高。另外一些知情交易者为了自己的利益，也会利用自己掌握的特定信息，可能会对此作出巨大的反应，使得股票价格往往会有跳跃的发生，甚至有极端的报复行为使价格发生大幅跳跃，极短时间内把价格直接拉到涨停或者跌停。也就说，噪声和跳跃发生是总会是同方向的，从统计角度看二者的关系是正相关的，而且是互为因果关系。
    另一方面，随着时间的推移和交易的进行，知情交易者将根据交易情况不断修正他们对所掌握特定信息的理解，一些噪音交易者也将从交易中不断推测和学习这些特定信息，再加上资讯传播的迅速，信息的不对称性大大降低。由于这些噪音交易者往往具有“追涨杀跌”倾向，必然造成交易量增加，交易活跃度提高，市场流动性水平也随着提高。同时，中国股市采用限价委托驱动的交易机制，交易活跃度提高使得大量竞争性的限价委托出现，这样有助于缩小买卖价差，交易信息连续性增强，交易离散程度降低，必然使得噪声程度降低，也会使得股票价格发生跳跃的可能性大大降低。也就说，流动性水平高的市场，发生跳跃的可能较小，噪声程度降低。从统计角度看，跳跃和噪声与流动性水平的关系分别是负相关的。
    由此看出，噪声、跳跃与流动性之所以呈现出这样的关系，根源于中国股市的现状和交易制度。
    5结语
    目前提高波动率的度量精度成为高频数据研究的焦点，而对于不同类型风险之间的内在联系的研究相对较少。因此本文从理论上与实证上分析了金融市场微观结构噪声、波动率跳跃、流动性之间的内在关系。以上证指数为例，本文选择方法分离出噪声、波动率跳跃并计算出流动性度量指标，对三者之间关系进行探讨。实证结果显示：（1）无论是未检验还是检验后的跳跃序列与噪声方差之间存在着显著地正相关关系，即这意味着噪声越大，波动率跳跃发生的可能性越高。由此可知在未能有效剔除噪声的情形下会导致市场上高估跳跃，因此若将噪声与跳跃同时考虑到波动率的度量当中，能够更好的度量市场的风险水平以及市场的异常风险；（2）从回归系数的符号上看，流动性与检验前与检验后的跳跃序列的关系都为负相关关系，流动与噪声之间的关系同样为负。这意味着流动性越大，上证指数的噪声越小，发生波动率跳跃的可能性越小。之所以会呈现这样的关系，原因在于中国股市现状和交易制度。
    三者之间的相关关系，反映出金融市场内部的噪声交易行为、异常风险与流动性风险之间存在着联系。因此，理清三者之间的关系能够更好的对市场的不同风险类型进行分类，从而更好地对市场风险类型及其内在联系机制进行识别，提高风险管理的水平。
        参考文献：
    [1]Zhang, L., Mykland, P., Ait-Sahalia, Y.. A tale of two time scales: Determining integrated volatility with noisy high frequency data[J]. Journal of the American Statistical Association, 2005, 100(472): 1394-1411.
    [2]Zhang, L.. Efficient estimation of stochastic volatility using noisy observations: A multi-scale approach[J]. Bernoulli, 2006, 12(6): 1019-1043.
    [3]Barndorff-Nielsen, O. E., Hansen, P. R., Lunde, A., Shephard, N.. Realised kernels in practice: Trades and quotes[J]. Econometrics Journal, 2009, 12(3): 1-33.
    [4]Jacod, J., Li, Y. Y., Mykland, P. A. et al. Microstructure noise in the continuous case: The pre-averaging approach[J]. Stochastic Processes and their Applications, 2009, 119(7): 2249-2276.
    [5]Barndorff-Nielsen, 0., Shephard, N.. Econometrics of testing for jumps in financial economics using bipower variation[J]. Journal of Financial Econometrics, 2006, 116(5):1-30.
    [6]Mancini, C.. Nonparametric threshold estimation for models with stochastic diffusion coefficient and jumps[J]. Scandinavian Journal of Statistics, 2009, 36(2): 270-296.
    [7]Andersen, T. G., Dobrev, D., Schaumburg, E.. Jump robust volatility estimation using nearest neighbor truncation[R]. Federal Reserve Bank of New York Staff Reports, 2010.
    [8]Christensen, K., Oomen, R., Podolskij, M.. Realized quantile-based estimation of integrated variance[J]Journal of Econometric, 2010, 159(1):74-98.
    [9]Jiang, G. J., Oomen, R. C. A.. Testing for jumps when asset prices are observed with noise: A "swap variance" approach[J]. Journal of Econometrics, 2008, 144(2):352-370.
    [10]Lee, S., Mykland, P.. Jumps in financial markets: A new nonparametric test and jump dynamics[J]. Review of Financial Studies, 2008, 21:2535-2563.
    [11]Ait-Sahalia, Y., Jacod, J.. Testing for jumps in a discretely observed process[J]. Annals of Statistics, 2009, 37(1): 184-222.
    [12]Ait-Sahalia, Y., Yu, J.. High frequency market microstructure noise estimates and liquidity measures[J]. Annals of Applied Statistics, 2009, 3(1): 422-457.
    [13]Andersen, T., Bollerslev, T., Diebold, F.. Roughing it up: Including jump components in the measurement, modeling, and forecasting of return volatility[J]. Review of Economics and Statistics, 2007, 89(4): 701-720.
    [14]Lahaye, J., Laurent, S., Neely, C. J.. Jumps, cojumps and macro announcements[J]. Journal of Applied Econometrics, 2010.
    [15]Jiang, G. J., Lo, I., Verdelhan, A.. Information shocks, jumps, and price discovery: Evidence from the U. S. treasury market[J]Journal of Financial and Quantitative Analysis, 2011,46:527-551.
    [16]Giot, P., Laurent, S., Petitjean, M.. Trading activity, realized volatility and jumps[J]. Journal of Empirical Finance, 2010, 17(1): 168-175.
    [17]Bandi, F., Russell, J.. Separating Microstructure noise from volatility[J]. Journal of Financial Economics, 2006, 79(3): 655-692.
    [18]孟卫东，杨万里.连续竞价市场个股流动性的度量方法、指标与模型[J].当代财经，2006，(8)：22-26.
    [19]Amihud, Y., Mendelson, H., Pedersen, L. H.. Liquidity and asset prices[J]. Foundations and Trends in Finance, 2005, 1(4): 269-364.
    [20]攀登，施东晖.中国个人投资者采用股价趋势交易策略的经验研究[J].世界经济，2003，(11)：71-77.
    [21]刘庆富，许有传.国内外非同步期货交易市场之间的跳跃溢出行为：基于风险事件的视角[J].系统工程理论与实践，2011，(4)：679-690.^