内容提要:Bongaarts和Feeney提出的去进度效应总和生育率引起了学术界广泛争议、讨论和各种新的尝试。文章梳理了这一研究上的理论争论,简要介绍在此方法方面的重要进展。十年来,去进度效应方法的应用已经从总和生育率扩展到平均预期寿命以及时期婚姻指标。文章还简要介绍了Yamaguchi和Beppu在改进去进度效应生育指标时的重要发现及其研究思路的创新。文章特别介绍了Bongaarts和Sobotka的最新研究成果,他们新提出了TFRp[*]指标,用以分析欧洲国家近年生育率的回升,发现TFR回升的主要原因是时期效应的减少和消失,而时期生育的数量水平其实相当平稳。在此就时期调整指标方面研究的进展做些评论,并讨论需要进一步思考的问题。
关键词:生育水平/时期指标/队列指标/进度和孩次构成效应
作者简介:郭志刚,北京大学中国社会发展研究中心研究员、社会学系教授,北京100871
1问题与背景
20世纪90年代,低生育率成为一个区域性和世界性的问题,在除美国外的其他欧、美、大洋洲的发达国家以及东亚一些新兴国家和地区,总和生育率(TFR)已经降至远低于更替水平。1997年时,全球已经有51个国家和地区、44%的全球人口处于低生育水平,联合国为此曾于1997年专门召开了专家会议,讨论低生育水平的问题。Bongaarts和Feeney(1998)指出,常规TFR会因为时期中生育年龄变化的影响(即时期进度效应)而产生显著的失真。而当时几乎所有低生育率人口同时存在着显著的生育年龄推迟,意味着这些人口的很低TFR水平在相当程度上是因为进度效应的扭曲。Bongaarts和Feeney(1998)建议了一种去进度效应总和生育率指标(TFR*)①,以便测量在如果没有进度效应时时期生育的数量水平(fertility quantum)②,进而还可以根据TFR*与TFR之差来测量时期进度效应的扭曲幅度。这种方法并不要求太多的数据,计算方法也很简单,但是却提供了一个新的视角来认识低生育率的形成。这一方法在后来的文献中常被简称为B-F方法。
针对TFR经常被同时当作队列终身生育率的表征,B-F方法原创者旨在用这种方法的分析结果说明,当时极低TFR水平是因为受到了进度效应的扭曲,但并不意味着这些人口的终身生育水平将会同样之低。B-F研究提供的应用例证是美国和中国台湾,分析结果揭示出,尽管这两个人口的TFR已远低于更替水平,但去进度效应后的TFR*却仍然在更替水平附近。尽管原创者并未明确地说,但给人的印象是他们也许认为生育率转变下降到更替水平会自然停止。于是,后来很多研究对此提出了批评,因为更多的实际数据测算揭示出,即使采用TFR*测量的生育水平也并没有在更替水平处停止,而是下降到了更低水平。B-F研究在理论和方法角度引发了国际人口学界一系列的激烈争论和相关研究,因而极大地推动了这一方面的理论探讨、方法改进和实际数据检验评价。
中国人口在20世纪90年代也进入了低生育率时期,多次全国人口调查结果反复显示出很低甚至是极低的生育率,然而当时人们基本否定了这样的结果,认为极低的生育率只是由于调查中严重出生漏报导致的虚假统计。但是,笔者较早认识到B-F方法提供了认识低生育率的新视角和定量方法,于是便在国内介绍了B-F研究的重大学术价值与实际意义,并全文翻译了原创论文,认为B-F方法的新视角不仅有助于推进对中国低生育率的认识,而且也有助于更好地认识我国以往的计划生育史和生育转变史(郭志刚,2000)。
十多年来,国内对去进度效应方法同样有不同看法,有关讨论间或有之(郭震威,2000;姜全保,2006;郭志刚,2006)。最近的一篇是郝娟和邱长溶(2012)用中国生育数据对TFR*进行了检验与讨论,检验的结果自然不好。其主要原因之一,正如大量文献所批评过的那样,是TFR*指标本身的确存在缺陷,导致其敏感性强、波动性大。笔者同时认为,检验结果不好也可能有数据缺陷的原因。这两方面的问题都很重要,都需要专门的研究与探讨。
笔者仅就数据问题做三点简要评论。第一,由于大量人口流动,且以青壮年为主,近年全国人口变动抽样调查以及其他全国人口抽样调查都显示出对青壮年流动人口存在明显遗漏(郭志刚,2010)。第二,该研究所用数据实际上来自于全国人口普查、全国1%人口抽样调查以及各年度人口变动调查(抽样比约为1‰)。这些调查的覆盖面不同,数据方面的偏差特点也有所不同。笔者也曾经做过一些尝试性分析,发现将这些不同来源数据构成一个系列后,无论是生育率还是平均生育年龄都存在明显的波动,分孩次以后波动更大,并且最大的波动存在于不同类型调查的衔接年份。第三,至于将生育数据再划分为城乡,那么由于乡→城人口流动以及城→乡的回流,城乡两者分别都不再是封闭人口,因此由于城乡序列各自的一致性,自然问题更复杂。
笔者注意到,郝、邱论文中索引的文献都是好几年以前的,特别是该研究认为去进度效应时期指标主要问题是因现实不满足调整核心公式的假定条件以至平均生育年龄不能反映真实进度效应变化,这种看法类似于以往文献的批评,然而却与最新研究的实证研究结论正好相反。因此,笔者觉得当务之急还是先介绍一下国际学术界在这一方面研究的最新进展,以便使我们自己的研究和探讨能够建立在一个更新更好的基本框架之上。去进度效应研究在学理与操作两个层面都极为复杂,文献甚多,而本文目的则是在有限篇幅里对最主要的新进展做一尽量通俗易懂的勾勒,并加以简要评论。
2对去进度效应方法的主要批评和其他尝试
B-F研究自1998年一发表,即引起热烈争论,争论焦点在以下几个方面。首先,从实际应用角度的批评。许多学者用实际数据应用和检验TFR[*]指标后,均发现其结果对平均生育年龄过于敏感,导致其波动甚大,甚至导致难以捕捉变化趋势。接着,学者们便追究效果不好的原因。这导致了多种并存的理论和方法上的研究和探讨。比如,所谓进度效应的本质到底是队列变化效应还是时期变化效应。又比如,进度效应是否一定造成偏差,以及应该用什么作为参照去测量时期效应。再有,TFR[*]指标的本质到底是时期真实生育水平的量度,还是通过时期生育特征测量对终身生育水平的一种估计。有的学者认为B-F方法虽然简单,但背后的假定却过于简单生硬,难以反映更为复杂的实际情况,于是尝试更复杂的方式来测量进度效应,试图弥合模型结果与实际结果的背离。当然,也有学者根本否定B-F方法及TFR*指标,认为其无论在学理上还是实用中都没有什么意义。毫无疑义,这些批评、讨论和新的尝试都是进度效应研究发展的推动力。
很多争论发生在去进度效应的调整指标到底是在测量什么这个问题上。Bongaarts和Feeney(2006)称根据时期孩次别平均生育年龄变化推算出来的调整因子(1-r)为“时期失真指数”。要是深究一步,所谓时期指标TFR失真的参照标准到底是什么?原创者的回答是在TFR基础上用时期失真指数调整出来的去进度效应TFR[*],因为所谓进度效应偏差就是TFR与TFR[*]之间的差。那么,TFR[*]又是什么,原创者认为它是一个反事实的时期生育的纯数量水平,即不存在进度扭曲时的时期生育的数量水平。那么,证明TFR[*]或类似的其他调整指标是否较好地反映时期生育的数量水平的标准又是什么?尽管这些调整指标是否趋势稳定可以反映自己的信度,但是它们却不能自己证明自己的效度更好。于是,方法论上的逻辑便出现了断裂,我们要测量一个东西,而又无法检验这种测量好不好,因为这个东西在现实中不存在。
如果回到最早人口学中关于TFR指标的进度效应失真,其实说的就是在终身生育率CFR不变的情况下,由于时期进度变化,TFR会偏离CFR。但是,TFR*原创者却一直明确否认去进度效应指标不是对终身生育水平的估计。笔者猜想,这大概是因为具体测量指标尚存在较大缺陷,其效用仍与研究目的相距过大。关于调整指标TFR*到底在测量什么上的含糊性就成了引发早期批评和反批评的焦点(Kim and Schoen,2000;Bongaarts and Feeney,2000;Van Imhoff, 2000,2001;Zeng and Land,2002),而且在后来也一直延续着。
总之,国际学术界对于B-F方法的批评可以简单划分成两大类。第一类态度是基本否定B-F方法,或者认为其逻辑有误,或者认为这根本是做不到的,或者认为这类研究并无实用价值。第二类态度则是基本肯定B-F方法的逻辑,认为这类研究有用,甚至是意义重大,但B-F方法存在缺陷、需要改进,或者需要另辟蹊径建立新方法。Luy(2010)对进度效应研究的本质进行阐发,而且对不同观点进行了比较详细的评论。他认为,“无疑,现有在生育和死亡方面的进度调整方法还存在一些缺陷,下一步的研究应该以改进这些技术为目标。……然而,没有一种批评B-F方法的理由能比存在进度效应的问题更为严重。真正的问题是,在什么时候、什么样的条件下,应该用进度调整指标来替代或辅佐常规时期指标(p438)。”笔者很同意Luy对进度效应研究的这种判断。
按笔者的梳理,从B-F方法自1998年提出以来,进度效应研究上不光有争论和批评,而且在以下方面取得了重要的实质性进展。
第一,进度效应问题并不局限于时期生育指标,而且普遍存在于人口各方面的时期指标上。
常规人口学指标体系尽管看起来已经完备定型,但在学理上其实仍然存在许多不足。最容易得到的是时期指标,其实用性也特别强。但是,几乎所有主要人口方面最基本的年龄别时期指标最终都是通过假设队列的方式来取得经典的概括性指标。在生育方面就是常规的总和生育率,在死亡或寿命方面就是人口平均预期寿命,与此类似的还有总和迁移率、总和结婚率等等。为什么非要把时期指标以队列口径反映出来呢?其原因是为了用以往的人口规律性来预测人口发展,比如,总和生育率和平均预期寿命都是最基本的人口预测参数。
既然常规总和生育率可能受到进度效应的影响,那么同理,按照假设队列方式建立的人口平均预期寿命指标自然也可能受到进度效应的影响。Bongaarts和Feeney(2002,2003)提出了对常规预期寿命指标的进度效应调整问题。顺便提一句,婚姻方面也已经有进度效应调整的研究(Winkler-Dvorak and Engelhardt,2004;Bongaarts and Feeney,2006)。
笔者曾在2003年参加的一次国际学术讨论会上听到Bongaarts本人介绍其对平均预期寿命指标的去进度效应研究,席间很多学者表示了异议。有学者认为,如果说生育是多次重复事件,生育时间表发生变化可能带来时期进度效应还尚可理解;而人的一生只经历一次死亡,那么进度效应如何表现?笔者当时觉得这个问题对平均预期寿命也存在进度效应的逻辑具有强大的颠覆力。但是后来笔者想明白了。其实对于一名妇女而言,一孩生育在其一生中也只可能有一次,所以这一事件与死亡一样也具有不可重复性。既然分孩次TFR(1)会受进度效应影响,那么同理,平均预期寿命指标自然也可能受到进度效应影响。
本文并不想具体介绍Bongaarts和Feeney将去进度效应方法引入平均预期寿命方面的细节,而是想说明两点:首先,进度效应问题是多种时期人口概要指标所共有的问题,因此这一方法对人口统计具有更为普遍的意义。其次,从笔者现在的理解来看,其实当Bongaarts和Feeney将去进度效应研究引入寿命研究以后,就已经隐含着他们已经找到了解决TFR[*]指标的内在缺陷的正确途径。而且,这与笔者自己的一个长期未解的疑惑也紧密相连。笔者在回应姜全保(2006)对年龄别递进比和TFR*指标理解的文章的脚注③曾经提到过常规人口预测中的这种不对称,即人口死亡或存活的预测用的是生命表中的死亡概率或存活概率,而在生育预测上却没有相应的转换,直接使用年龄别生育率。
也就是说,TFR[*]的实用效果不好,主要并不是像有的学者批评的那样,是因为用平均生育年龄来表示进度变化过于简单化。问题的根源其实在于调整对象TFR指标自身还存在着另外的基础性缺陷,而这些缺陷只靠调整进度变化效应是不能被消除的。这个缺陷则源于在建构TFR时,生育率没有被转换为生育概率。于是,由这一点引发了下面的研究进展。
第二,进度效应偏差的构成和产生原因要比B-F方法设想的更复杂。
简而言之,常规总和生育率是年龄别生育率的直接合计,因此这种指标不是风险概率(hazards,又称第一类率)的概括,而是事件发生率(incidence rate,又称第二类率)的概括。由于经过生命表这种转换,所以平均预期寿命指标是对一套风险概率的概括。然而,当Bongaarts和Feeney将去进度效应方法应用于平均预期寿命调整时,便已经自然而然地摆脱了最初创建的TFR[*]指标基于发生率所含的另一个以前未被认识的偏差问题。
近30多年来,国际学术界出现了人口统计与通用统计日益打通的趋势。比如,用泊松回归对某一年数据取得的离散年龄的回归系数就是年龄别生育率;又比如,回归分析与生命表的结合产生了事件史分析。在通用统计中,发生率与风险率两种概念的差别非常清晰。著名的事件史方法专家K. Yamaguchi与另一位作者M.Beppu的参与有力地推进了生育指标的进度效应研究。
Yamaguchi和Beppu(2004)认为常规TFR指标存在两个问题:第一个问题是人口学界已知的,即TFR的基础不是概率的集合,才会导致TFR(1)>1这种不正常的统计现象,所以常规TFR指标的效度较差,不能很好地测量时期总和生育水平这个理论概念。第二个问题在以往文献中从未提到过,也是该研究的主题,即在时期TFR指标存在进度效应时,其实进度效应中包含着两种不同成分:一种是真实进度偏差,即队列终身生育率CFR与有效的时期总和生育水平测量值之间的差,但它通常只能在强假定之下来估计。另一种是虚假进度偏差,即常规TFR指标由于是将生育事件发生率当作风险率来用,因而在生育进度变化时所产生的系统性偏差。
简而言之,常规的年龄别生育率的分母是本年龄的全部妇女数,而分子是本年龄妇女所生育的子女数,计算分孩次的年龄别生育率时,分母仍是该年龄全部妇女数,只是将分子换成所属孩次的生育数。其实,已经生育了二孩的妇女便不可能再生一次二孩了,也就是说已经生育了两个及以上孩子的妇女根本不存在再生育二孩的风险。所以,计算二孩生育风险率时分母就不能包括已经生育过两个及以上孩子的妇女。如果再严格一点,尽管存在多胞胎或一年生育两次的情况,一般而言,其实从未生育过的妇女也不大可能一步跳到生育二孩,因此计算这种更严口径的某一孩次生育风险率时的分母只能是本年龄那些已经生育过前一孩次但尚未生育这一孩次的妇女。后者就是年龄别孩次递进比。换句话说,生育的发生率和以上所述两种风险率的差别在于它们分母的定义不同。在统计学中,前一种风险率称为不可重复事件的风险率,只要尚未经历该孩次生育事件的妇女都视为历险人口。而后一种风险率则称为可重复事件风险率,只有处于前一孩次妇女才是下一孩次生育的历险人口。而与生育风险率相对的则是留存率,即在风险期内不发生生育的概率。与上述两种生育风险率相对,留存率也有两种。Yamaguchi和Beppu的研究分别在这两种生育事件留存率的基础上尝试建立了两种时期生育总和生育水平指标,以及相应的去进度效应指标。
Yamaguchi和Beppu的研究证明,真正的风险率总是大于发生率,因此基于生育率基础上的常规TFR测量值总是会低估按理论定义的真实的时期生育水平。并且,由于虚假进度偏差的方向与真实进度偏差的方向一致,所以虚假进度偏差的存在使总的进度效应膨胀。这个研究还通过公式推导证明,将生育率当作风险率来用还存在另一个重大的缺陷,它的失真并不仅仅是由于本年的进度变化,而且还依赖于以前年份进度效应的积累。
笔者认为,Yamaguchi和Beppu的研究独到地揭示出常规TFR存在的两种不同成分的进度效应,以及虚假进度效应还依赖于以往进度效应的积累,并导致总的进度效应膨胀,这些分析实际上比较清楚地解释了,为什么B-F方法建议的TFR[*]的实际应用效果并不太好,即它的结果很不稳定。
更重要的是,他们从理论上和日本生育数据的应用分析结果证明,当改用真正的时期风险率来取代发生率时,不需要再做任何强假定便可以消除虚假进度偏差,取得一个效度更高的时期生育水平测量指标,进而可以更准确地测量真实进度效应的幅度。他们对基于上述两种生育风险率的时期生育指标均进行了试验和讨论,但是作为进度调整指标,他们建议用第一种(即不可重复事件)风险率的指标为好,因为它与终身生育率CFR的关系比较明确,而且它的结果也较为可靠。
3生育调整指标的最新发展
Bongaarts和Sobotka(2011,2012)新近提出了一种进度与孩次调整的总和生育率指标(tempo-and parity-adjusted total fertility rate,标注为TFRp[*],沿用文献习惯,简称为B-S方法或B-S研究)。在Bongaarts和Feeney将进度效应研究引入生命表的平均预期寿命方法的基础上,将其思路重新引入生育率研究,并且用这一新方法应用于4个数据可得的欧洲国家(捷克、荷兰、西班牙和瑞典),旨在分析和解释欧洲国家近年来常规TFR水平的回升。
生育率分析方法中本来就有与生命表类似的生育表分析方法,它描述了一个假设队列从初始状态(全部尚未生育时)起随年龄(或按结婚及各次生育之间的间隔年数)而发生各孩次生育的概率,同时也反映了尚未生育各孩次的留存概率。B-S研究依据生育表概率建立新的生育指标并加以失真(distortions,即进度效应和孩次结构效应的统称)调整的原理与上述Yamaguchi和Beppu(2004)用留存概率建立生育指标的原理是相通的。按笔者理解,B-S方法所说的孩次结构效应调整其实就是在排除Yamaguchi和Beppu所说的TFR中含有以前年份进度效应积累的问题,因为一个时期妇女的孩次结构状况是由以前多年的生育所决定的。这两项独立的研究殊途同归,他们对B-F方法的TFR[*]进行改进的本质就是用生育概率取代了生育率。
B-S方法将各次生育视为分别的不可重复事件来计算年龄别风险概率,而这也正是Yamaguchi和Beppu所建议的。这种风险率的分母是该年龄所有尚未生育过孩次i的妇女,即处于孩次i-1、i-2、……、0上的所有妇女。B-S方法在这种生育概率基础上,先建立了TFRp指标取代常规TFR指标来测量时期总和生育水平,其收益是排除了常规TFR指标中存在的孩次结构变化效应。
B-S方法仍然沿用时期孩次别平均生育年龄的变化指数(1-r[,t,i])来代表进度变化,但是在应用它来调整时期生育率的方式与B-F方法有所不同,最后取得新的调整指标TFRp[*]。
B-S研究应用TFRp[*]指标对若干欧洲国家生育数据进行了分析。作为比较,研究中同时应用了另外两种调整指标。其一是颇具争议的B-F最初的调整指标TFR[*]。其二是由Kohler和Ortega(2002)提出的另一种调整指标(PATFR[*]),其建构基于对TFR[*]指标的一种主要批评,即TFR[*]的调整中并未考虑妇女人口中的孩次结构变化(Van Imhoff and Keilman,2000;Kohler and Ortega,2002;NíBhrolcháin,2011)。PATFR(即Parity and Age TFR)是由Rallu和Toulemon(1994)提出,建构于可重复事件风险率(即年龄别孩次递进比)模型之上。而PATFR[*]即在PATFR基础上进行进度效应调整,其调整因子则是按年龄别风险率的平均年龄变化来测量。
计算结果(见图1,即原文图10)表明:TFRp[*]的水平相当稳定,显著优于TFR[*]和PATFR[*],也就是说在B-S方法的一系列改进的确提高了测量的可靠性。这也就表明,TFR[*]剧烈波动的主要原因并不在于用分孩次平均生育年龄来测量时期进度效应,因为TFRp[*]在这一方面与其并无变化。而PATFR[*]的水平相对较低,与常规TFR值的差相对较小,也就是说,它的去进度效应的效果并不太好,并且它的波动还相当大。
如前所述,稳定性反映的是测量的信度要求,一个指标稳定性较高并不能说明这个指标就好,更重要的是它的效度要高,也就是说它必须正确反映它所要测量的事物。那么,去进度效应指标到底要反映什么,用什么作为标准来测试这些去进度效应指标的效度呢?实际上,这个问题一直在困扰去进度效应研究。
在Bongaarts和Sobotka(2012)的论文中专设了一节来讨论时期生育率与队列生育率的比较。作者指出,TFR[*]旨在从常规TFR中消除进度效应,而PATFR[*]和TFRp[*]除了消除进度效应外,还同时要消除妇女孩次结构变化的效应。如果能够很好地消除这两种时期效应,调整指标便是时期生育数量水平的估计,它们是纯粹的时期指标。这类调整指标既不是要预测队列终身生育率,也不是要预报未来的时期生育率。
然而Bongaarts和Sobotka(2012,p103)接着就指出,在一定的条件下,比较队列生育率与去进度效应时期生育率是合理的。比如,当队列终身生育率CFR不变时,由于存在时期扭曲效应,TFR会变化,而调整指标则会保持稳定,而且会等于CFR。当然上述条件还需要假定,时期生育率的年龄分布形状不变,并且妇女的孩次构成随着生育进度表而变化。在当代欧洲人口中,队列生育率变化很慢,没有显著波动,而时期生育率的分布形状也变化很小,因此这时进度效应就成为导致时期生育率和队列生育率之间差异的主要因素。在这种情况下,用较长一段时期调整时期指标的平均数(以避免年份指标波动影响)与队列指标的比较,有助于评价哪一种进度调整指标更好。
图1不分孩次的观测和各种进度调整的总和生育率
Figure 1Observed and Tempo-adjusted Total Fertility Indexes for All Birth Orders
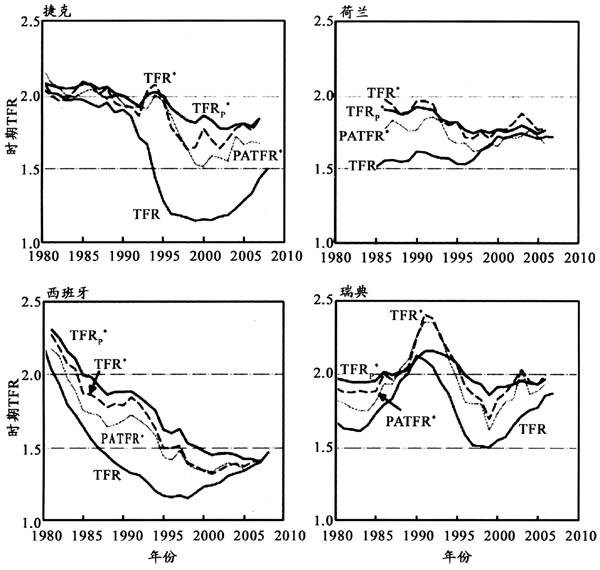
资料来源:直接引自Bongaarts和Sobotka(2012)论文的图10(Bongaarts,John and Tomas Sobotka.2012.A Demographic Explanation for the Recent Rise in European Fertility. Population and Development Review 1:102)。
B-S研究总结了以往此类比较的经验,认为最好将一定时期的进度调整指标值与那些在同时期内已达平均生育年龄妇女队列滞后取得的终身生育率值相比较,于是该研究采取的方式是对C年出生队列的终身生育率与t年的修匀时期调整指标进行比较。比如,如果1969年出生队列的平均生育年龄为30岁,那么就用这个队列的终身生育率与(1969+30=)1999年的调整指标比较,而1999年时期指标值就简单采用该指标的5年移动平均数。他们这种比较结果(见图2,即原文图11)表明,参加比较的5种生育指标总体上存在着的关系。除了捷克结果中TFRp[*]略偏高外,其他国家的TFRp[*]都非常接近终身生育率CFR,并且TFR[*]相对来说也还不错,尽管PATFR[*]与CFR之差较大,但是仍然显著高于常规TFR水平,说明它也确实起到了消除常规TFR中时期偏差的一定作用。
图21967年(捷克为1968年)出生队列的终身生育率CFR与该队列达到平均生育年龄的年份时3种调整的生育指标及常规时期TFR的比较
Figure 2Comparison of the Completed Fertility Rate(CFR)among Women Born in 1967 with Three Adjusted Fertility Indicators and with the Conventional Period TFR in the Year this Cohort Reached the Mean Age at Childbearing
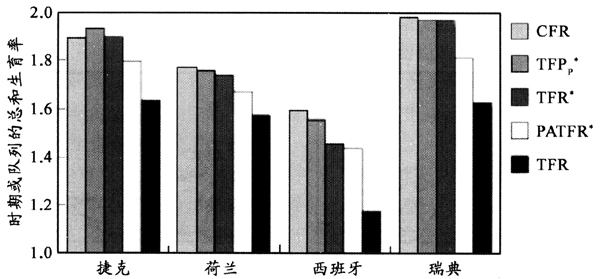
资料来源:直接引自Bongaarts和Sobotka(2012)论文的图11(Bongaarts,John and Tomas Sobotka. 2012. A Demographic Explanation for the Recent Rise in European Fertility. Population and Development Review 1:104)。
B-S研究还细致地列表比较了这些指标在分孩次生育水平测量上的表现,所有四国结果中的所有孩次上,TFRp[*]与CFR都吻合较好,因此从消除进度和孩次构成的扭曲效应而言是最好的指标。孩次别调整指标的结果还说明,以前那种认为去进度效应指标会夸大时期生育水平的说法并没有得到证明。并且,TFR[*]指标和新提出的TFRp[*]指标都可以大幅度地消除常规生育率TFR与队列生育率CFR之间的差距,尤其是TFRp[*]的效果最好,消除了两者差距中的80%~90%。PATFR[*]指标在孩次1上的效果还不错,但是在较高孩次上的效果变得很差。B-S研究认为,PATFR的基础生育概率是严格递进性质的,高孩次的计算依赖低孩次的结果,因而可能逐级夸大较高孩次上进度影响。在其附录1中还提到,高孩次的PATFR计算值特别低,甚至低于常规TFR的水平③。在不分孩次、孩次1和孩次3上比较了各调整指标相比CFR的误差率后,Bongaarts和Sobotka(2012)认为:“正如在所有孩次上的情况一样,TFRp[*]对各国孩次3的生育度量也是最好的,其表现远超过了我们的期望”(p107)。4从TFRp[*]指标看近年欧洲TFR水平的回升
对于近年欧洲国家TFR水平回升,人口学方面有两种视角的解释:其一是从时期因素出发,认为由于更早一段时期生育年龄不断推迟的势头在近十几年中显著减缓,因而时期进度效应的减小使TFR水平向真实数量水平回归。其二是从队列因素出发,认为当妇女队列处于较晚生育年龄时,会促使其将以前推迟的生育做弥补性完成。前者的依据是时期生育年龄推迟减缓,后者的依据是高龄生育者显著增多。
Bongaarts和Sobotka(2011,2012)的研究目的是分析和认识欧洲国家近年TFR水平的回升。他们对上述争论的看法是:第一,时期因素为主的观点其实与队列视角的推迟-弥补解释是完全一致的,因为时期和队列不过是同一事物的两个侧面,两者不可能断然分开。第二,这两种解释争论的焦点在于哪一个是欧洲生育率回升的主要原因。第三,实际上这两种单纯视角都不足以解释欧洲生育率回升。比如,即使在TFR长期没有变化时,背后也完全可能存在时期生育进度变化或者是队列的推迟-弥补现象。
图3近年欧洲10个国家的时期TFR回升与其他去进度效应指标的比较
Figure 3Period TFR during the Phase of Its Recent Increase as Compared with Two Tempo-adjusted Indicators in Ten European Countries
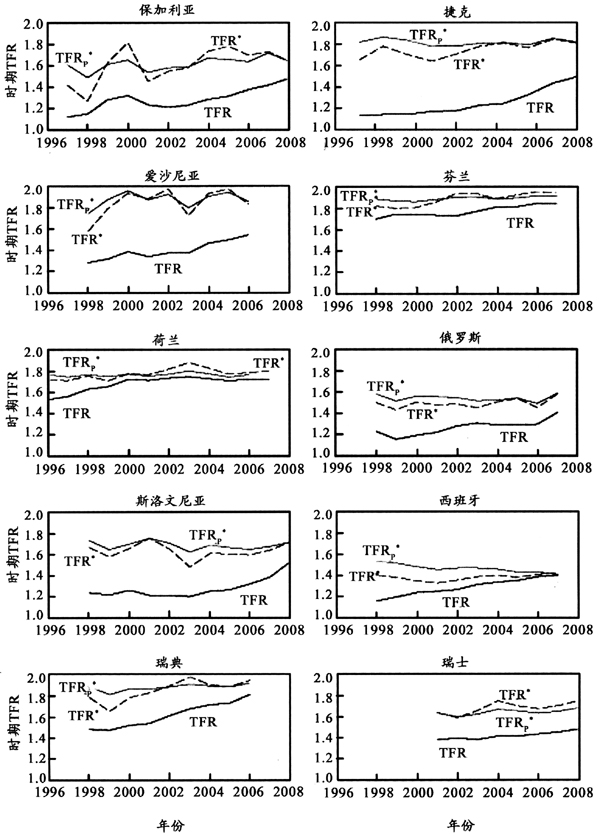
注:直接引自Bongaarts和Sobotka(2012)论文的图12(Bongaarts,John and Tomas Sobotka. 2012. A Demographic Explanation for the Recent Rise in European Fertility. Population and Development Review 1:108)。
实际上,B-S研究在提出新的TFRp[*]指标之前花了相当大的篇幅用模拟结果证明上述两种视角的解释是同一问题的两个侧面,尽管从时期视角的反映和从队列视角的反映看起来有所不同。
当B-S研究在提出TFRp[*]指标并用4个国家的结果做了多指标比较检验后,便将分析扩展到更多的欧洲国家(见图3,即原文图12)。由于TFRp[*]指标可以很好消除进度效应,稳定地反映生育的数量水平,因而可根据它来判断TFR变化究竟出于什么原因,是生育的数量水平变化的反映,还是进度效应和孩次结构变化的影响。根据欧洲各国的生育指标图,B-S研究指出两点。第一,这些国家近年来TFR与TFRp[*]之间的差距都在日益缩小,意味着TFR内含的时期失真在减少。第二,大多数国家的TFRp[*]曲线呈水平状,反映生育的数量水平其实并没有变化。因此,最终结论就是,近年欧洲国家TFR回升的本质是进度效应减少或消除,而不是生育的数量水平在提高。根据B-S研究的计算,排除了瑞士以后④,另外9个欧洲国家近年TFR回升幅度中平均有81%可以归因于时期失真度的减少。
图中还提供了TFR[*]曲线,过去在没有TFRp[*]时,只能用这种缺陷明显的TFR[*]与TFR之间的差来反映进度效应幅度。通过比较,便能看出TFR[*]的缺陷对以前的认识或判断存在一定误导。B-S研究对此做了一些评价。其一,TFR[*]曲线很不稳定,波动很大,难以可靠地反映生育的数量水平,而TFRp[*]反映出生育的数量水平在近年中是很稳定的。其二,在各国TFR水平最低时,TFRp[*]水平都显著高于TFR[*]水平,这就表明以往根据TFR[*]值其实显著低估了当时生育的数量水平。其三,由于TFR[*]低估了生育的数量水平,因而又导致以前对进度效应幅度也显著低估了。
其实,图3中除了B-S研究已经总结的结论以外,我们还可以看出另外一些结果。第一,尽管近年来欧洲TFR明显回升,不仅TFR值远低于更替水平,而且经过失真调整能够较好代表时期生育数量水平的TFRp[*]值也仍然显著低于更替水平。换句话说,过低生育率仍然是欧洲人口发展前景的一个重大问题。第二,有的国家出现了TFR提高与TFRp[*]下降同时发生的现象,比如,西班牙和俄罗斯这种情况就很明显。
5思考与讨论
国际学术界对时期调整指标的争论和研究进展内容极为丰富,本文只介绍了其中的一部分成果,但并不意味着其他的研究成果就不重要。这些成果涉及基础理论、方法论和技术操作以及实际应用经验,全都值得我们认真学习、深入领会和努力掌握。他山之玉,可以攻石,有针对性地学习和借鉴学术前沿成果,可以使我们的研究拓展视角,少走弯路。
在时期调整指标方面仍然还有很多问题需要进一步讨论与思考。
首先,时期调整指标到底是在测量什么?实际上,在1998年的B-F研究中,就已经对CFR和TFR[*]进行比较了,采用与某队列CFR对应的35年TFR[*]的加权平均数来进行比较。在2012年的B-S研究中,对CFR和TFRp[*]的比较取得更确切的方式,用队列的出生年加上该队列平均生育年龄来确定该队列终身生育率应该作为与哪一个年份时期调整指标的参照标准,采用了5年移动平均数来加强时期指标稳定性。所以,尽管时期调整指标的本质的确是时期性质的假设队列指标,其实它与CFR之间有不能割断的联系。正是因为队列终身生育率意义重大,因为它反映的是人口再生产的关系。但它又是个“马后炮”指标,因此利用时期信息推导出时期调整指标,以及了解它在什么条件下近似等于哪些队列的终身生育率的研究才极为重要,因为这就是目前用时期数据所能得到的关于队列信息的最好估计了。
其次,即使用了时期调整指标,能够很好反映时期生育的数量水平,是否需要用TFRp[*]来取代TFR?笔者认为,应该不会。因为TFR本来就是个一身集二任的指标,它虽然会时而发生背离时期生育的数量水平,但是它与实际生育数量联系更紧密,而后者则与队列生育的数量水平联系更紧密。而且只有用它和时期调整指标的差才能表达时期效应偏差的幅度。所以,两者之间不是取代关系,而是相辅相成的关系。特别需要指出,进度效应导致TFR失真的说法只是就其相对于时期生育的数量水平(或者说是相对队列生育水平)而言的,而不是说TFR本身真的发生了什么虚假的统计错误。
再次,B-S研究对中国低生育率研究有重要启示。实际上,笔者将进度效应研究介绍到国内来就是为了说明出生漏报并不是人口调查的很低生育率的唯一原因,因为生育年龄推迟也可以导致TFR的显著下降。尽管尚未用TFRp[*]应用于中国数据,但是依据B-S研究的逻辑,笔者以前用TFR[*]估计的进度效应幅度也可能会显著低估,那么对低生育率的真实贡献可能更大。
最后,新指标TFRp[*]的计算方法并不复杂,但我们想应用它做中国生育研究先要解决一个困难,即目前并不完全具备计算所需的数据。计算TFRp[*]指标需要两种年度序列数据:(1)分孩次年龄别出生数。目前共同组成中国生育数据年份序列来源的是3种调查数据,即人口普查、1%人口抽样调查和各年度人口变动调查,三者都将这方面信息作为标准公布数据提供。(2)分孩次的育龄妇女年龄别人数。人口普查和1%人口抽样调查都提供这方面数据,但是年度人口变动调查并不提供。可是我们仅对普查或小普查年份来计算这个指标的意义不大,这个指标不能形成年份序列曲线,就无法用于监测和分析时期生育率变化的原因。另外,国家人口计生委的多次人口调查都包括回顾性生育数据,可以提供上述两种信息。但这种调查是每隔几年才做一次,数据也越来越难以得到。并且,这种数据往往只调查当前育龄妇女,那么回推以前年份时高龄育龄妇女的数据信息便会出现删截问题。再退一步,可以利用其他方法从现有数据推算出各年分孩次的育龄妇女年龄别人数,这是很有可能的。实际上Yamaguchi和Beppu(2004)的研究也遇到了类似的数据问题,可以借鉴他们的估计方法。
注释:
①在其1998年的原创论文中,这个指标曾标注为TFR’,后来国际学术文献中将其标注改为TFR*。
②注意,本文中所说的生育的数量水平并不是生育数或出生数。生育的数量水平指真实队列或假设队列的终身生育平均数,因而是相对数指标,而生育数或出生数则是指生育或出生的绝对数。
③如Yamaguchi和Beppu(2004)所述,真正的风险率高于发生率,所以高孩次PATFR值低于TFR值是不合理的。
④由于瑞士的TFR值变化太小,再去分解其中进度分量和数量分量的估计会相当不稳定。
参考文献:
[1]Bongaarts, John and Griffith Feeney. 1998. On the Quantum and Tempo of Fertility. Population and Development Review 2:271-291.
[2]Bongaarts, John and Griffith Feeney. 2000. On the Quantum and Tempo of Fertility: Reply. Population and Development Review 3: 560-564.
[3]Bongaarts, John and Griffith Feeney. 2002. How Long Do We Live? Population and Development Review 1: 13-29.
[4]Bongaarts, John and Griffith Feeney. 2003. Estimating Mean Lifetime. Proceedings of the National Academy of Sciences 23: 13127-13133.
[5]Bongaarts, John and Griffith Feeney. 2006. The Quantum and Tempo of Life-cycle Events. Vienna Yearbook of Population Research 2006: 115-151.
[6]Bongaarts, John and Tomas Sobotka. 2011. Demographic Explanations for the Recent Rise in European Fertility: Analysis Based on the Tempo-and Parity-adjusted Total Fertility. European Demographic Research Paper 4, Vienna Institute of Demography.
[7]Bongaarts, John and Tomas Sobotka. 2012. A Demographic Explanation for the Recent Rise in European Fertility. Population and Development Review 1: 83-120.
[8]Kohler, Hans-Peter and José A. Ortega. 2002. Tempo-adjusted Period Parity Progression Measure, Fertility Postponement and Completed Cohort Fertility. Demographic Research 6: 92-144.
[9]Kim, Young J. and Robert Schoen. 2000. On the Quantum and Tempo of Fertility: Limits to Bongaarts-Feeney Adjustment. Population and Development Review 3: 554-559.
[10]Luy, Marc. 2010. Tempo Effects and Their Relevance in Demographic Analysis. Comparative Population Studies 3: 415-446.
[11]Ní Bhrolcháin, Máire. 2011. Tempo and the TFR. Demography 48: 841-861.
[12]Rallu, Jean-Louis and Laurent Toulemon. 1994. Period Fertility Measures: The Construction of Different Indices and Their Application to France, 1946-89. Population, An English Selection 6:59-94.
[13]Van Imhoff, Evert and Nico Keilman. 2000. On the Quantum and Tempo of Fertility: Comment. Population and Development Review 3: 549-553.
[14]Van Imhoff, Evert. 2001. On the Impossibility of Inferring Cohort Fertility Measures from Period Fertility Measures. Demographic Research 5: 23-64.
[15]Winkler-Dvorak. Maria and Henriette Engelhardt. 2004. On the Quantum and Tempo of First Marriage in Austria, Germany, and Switzerland: Changes in Mean Age and Variance. Demographic Research 9:231-263.
[16]Yamaguchi, Kazuo and Motomi Beppu. 2004. Survival Probability Indices of Period Total Fertility Rate. Paper Presented at the Annual Meeting of the Population Association of America 2004, Boston.
[17]Zeng, Yi and Kenneth C. Land. 2002. Adjusting Period Tempo Changes with an Extension for Ryder's Basic Translation Equation. Demography 38: 269-85.
[18]郭震威.对“去进度效应总和生育率(TFR’)方法”的一点看法.人口研究,2000;1:19-21
Guo Zhenwei. 2000. Comments on the Tempo Adjusted TFR. Population Research 1:19-21.
[19]郭志刚.2000.从近年来的时期生育行为看终身生育水平——中国生育数据的去进度效应总和生育率研究.人口研究,2000;1:7-18
Guo Zhigang. 2000. Lifetime Fertility of Chinese Women: A Look at the Recent Period Fertility Behavior. Population Research 1: 7-18.
[20]郭志刚.孩次递进比的计算与调整生育指标的理解.中国人口科学,2006;5:84-88
Guo Zhigang. 2006. Calculating Parity Progression Ratios and Understanding Adjusted Fertility Rates. Chinese Journal of Population Sciences 5: 84-88.
[21]郭志刚.中国的低生育水平及相关人口研究问题.学海,2010;1:5-25
Guo Zhigang. 2010. China's Low Fertility Level and Related Issues to Population. Academia Bimestris 1: 5-25.
[22]郝娟,邱长溶.对去进度效应总和生育率的检验与讨论.人口研究,2012;3:81-88
Hao Juan and Qiu Changrong. 2012. Revisiting the Tempo Adjusted Total Fertility Rate. Population Research 3:81-88.
[23]姜全保.孩次递进生育指标和生育指标的调整.中国人口科学,2006;5:79-82
Jiang Quanbao. 2006. Parity Progression Fertility Indicators and Adjustment of Fertility Indicators. Chinese Journal of Population Sciences 5:79-82.^
