会员登录
会员注册内容提要：要素生产率提升是技术进步的效用结果和完整体现。本文引入效率体现式技术进步概念，以资本生产率与劳动生产率的综合指数来体现总体技术进步水平，构建经济增长中资本规模、劳动力规模和总体技术进步三因素贡献的分解模型，并利用中国1980—2010年的时间序列数据，对期间的技术进步贡献及其结构进行了实证分析。本文研究结果表明，经济增长的动力主要源于资本规模增长，劳动力投入规模贡献不大，技术进步贡献不小。技术进步贡献主要源于生产技术质量和生产技术效率，产业间劳动力构成和其他管理技术进步贡献微小。
关键词：效率体现式技术进步，生产技术质量，生产技术效率
作者简介：朱子云(1958—)，男，浙江丽水人，中国工商银行丽水分行总经理，高级经济师；朱土兴(1949—)，男，浙江丽水人，丽水学院教授。
一、引言
近十年来，有关中国经济增长效率问题引起理论界和实践部门的广泛关注。中国过去数十年靠资本和劳动高投入式增长是否是高效的，直接影响着未来经济发展方向的选择。近几年，国家创新体系建设和经济发展方式转变等发展战略的提出，无不与这个判断密切相关。根据经济增长理论，经济增长的来源可分为资本投入增长、劳动力投入增长和全要素生产率(TFP)增长3个部分。如何从经济增长中分解全要素生产率和技术进步贡献率？美国经济学家索洛(Solow)[1]提出了总量生产函数的概念，明确地将技术进步纳入生产函数中，在数量上建立了产出增长率、投入要素(劳动、资本)增长率和全要素生产率的关系，首次定量分离出了技术进步在经济增长中的作用，并因此获得诺贝尔经济学奖，从此测度TFP对经济增长的贡献就成了一个经久不衰的研究课题。由于TFP测算的重要意义，自中国改革开放以来，经济学界就不断有人利用各种数据与各种计量方法对中国经济TFP贡献进行测算。近几年对中国技术进步贡献的测算和分析又成为经济研究的热点，在国内外主流核心期刊上出现了大量关于TFP测算以及与TFP概念联系紧密的技术进步和技术效率测算文章。虽然大量文献在测算全要素生产率和技术进步贡献率方面已经进行较深入的研究，但下面5个方面问题在技术进步贡献率分解中至关重要，而有关文献却少有涉及。
其一，大多研究者在经济增长分解的回归方程中，将分解因子列为资本、劳动力以及全要素生产率(或技术进步贡献)，如曹吉云[2]、易纲等人[3]、华冬芳和李智勇[4]的研究。也有的研究者在回归方程中加入产业结构、资本集聚、人力资本等因素，如徐瑛等人[5]、熊俊[6]的研究。然而，在分解全要素生产率(或技术进步)的回归方程中，资本和劳动力投入规模扩大的贡献程度会伴随所纳入分解因子数量的多少而发生变化，并导致全要素生产率测算结果的巨大差异。尽管加入产业结构、资本集聚、人力资本等因素进行分解比仅纳入资本投入规模、劳动力投入规模要合理一些，但是产业结构、资本集聚、人力资本等因子与资本投入规模、劳动力投入规模并非同一层级因子，将它们列为同一层级因子进行分解不仅在理论上缺乏科学合理性，而且在实践上势必将导致分析结果的失真。
其二，一些文献在分解技术进步贡献中，以第三产业劳动力占比作为技术水平的替代变量来求解逐期变化的产出弹性，如曹吉云[2]、陈瑾瑜[7]的研究。然而，众所周知，第三产业劳动力占比作为技术水平的替代变量，无论是理论上还是客观现实上都是缺乏令人信服之依据的。
其三，有些文献在分解技术进步贡献时，将总产出方程中的资本因子拆分成建筑资本因子和设备资本因子，并据以求解出资本体现式技术进步贡献和中性技术进步贡献，还测量出资本体现式技术进步贡献占资本贡献的比重，如宋冬林等人[8]、孙克[10]的研究。然而，众所周知，第三产业劳动力占比作为技术水平的替代变量，无论是理论上还是客观现实上都是缺乏令人信服之依据的。
其四，大多数文献在构造技术进步贡献分解方程时将资本产出弹性与劳动产出弹性之和等于1，即α+β＝1，也就是规模报酬不变，如赵志耘等人[10]、辛永容等人[11]的研究。然而，在现实经济生活中，真的有必要假设吗？需要深入反思。
其五，传统总量生产函数(技术进步A、资本K和劳动力L)中，资本K、劳动力L对总产出的弹性系数依次为α，β，且通常α≠1，β≠1，可是技术进步对总产出的增长却没有设定弹性系数或者说隐含了其产出弹性等于1。也就是说，技术进步1个百分点，就使总产出增长1个百分点。然而，现实经济生活中，技术进步对总产出的增长却同样存在弹性，且弹性系数通常不等于1，甚或远远偏离1。
本文的创新之处在于，关注资本和劳动力质量、效率，引入效率体现式技术进步概念，以资本生产率与劳动生产率的综合指数来体现总体技术进步水平，据以构建经济增长中资本规模、劳动力规模和总体技术进步三因素贡献的分解模型，据以分解出资本规模贡献、劳动力规模贡献和总体技术进步贡献。引入技术质量和效率概念，以设备资本生产率与高技能劳动生产率的综合指数来体现生产技术效率水平，构造总体技术进步贡献中生产技术质量、生产技术效率、劳动力空间构成和其他管理技术进步四因素贡献的细分模型，据以分解出生产技术质量贡献、生产技术效率贡献、劳动力空间构成贡献和其他管理技术进步贡献，从而可以更加准确地判断中国经济增长源泉和各类技术进步的贡献程度，正确分析各类技术进步在推动经济增长中的优势与劣势、长板与短板，进而为合理选择更加有效的技术进步路径提供理论依据。
二、构建可检验的双层分解模型
本文的工作是循着经济增长思路和技术进步构成，建立可检验的双层分解模型。
(一)第一层次分解模型：基于效率体现式技术进步的经济增长分解
所谓效率体现式技术进步，是指融合在资本生产率和劳动生产率提升过程中的生产技术进步与管理技术进步的综合反映。生产技术进步体现为资本质量和劳动力质量与能量的综合提升，管理技术进步体现为资本和劳动力的配置结构优化、潜能发挥增强、利用有效性提高。
假定总量生产函数为：
Yt=AtηKtαLtβ (1)
式(1)中，Yt，At，Kt，Lt分别为第t期的实际产出、效率体现式技术进步指数、资本投入规模、劳动力投入规模。α，β分别为资本投入和劳动力投入的产出弹性，η为效率体现式技术进步的产出弹性。
要素生产率提升是技术进步的效用结果和完整体现，技术进步对经济增长的一切作用都会在资本生产率和劳动生产率提升中表现出来。据此，可以假设效率体现式技术进步指数At与资本生产率和劳动生产率的综合指数Ut之间存在指数函数关系，即Atη＝Utb，由于经济系统中前后时期之间存在着资本生产率差异和劳动生产率差异，因而指数方法对于解析其效率替代式技术进步将更有说服力。这一假设，其理由有四：第一，资本生产率和劳动生产率的综合指数是生产技术进步水平的综合反映，老产品功能创新和新产品开发、劳动工具和生产工艺改进、资本装备水平和劳动者劳动技能提高对全要素生产率提升的贡献作用，都会通过资本生产率和劳动生产率的综合指数得以全面反映。第二，资本生产率和劳动生产率的综合指数是微观经营管理水平的综合反映，微观经营管理改善对全要素生产率提升的贡献作用，都会通过资本生产率和劳动生产率指标的综合指数得以全面反映。第三，资本生产率和劳动生产率的综合指数是宏观政策和管理水平的综合反映，宏观产业政策、行业政策、区域政策、货币信贷政策、财政税收政策等诸方面改进对全要素生产率提升的贡献作用，都会通过资本生产率和劳动生产率的综合指数得以全面反映。第四，资本生产率和劳动生产率的综合指数还可以全面反映行业劳动力结构与资本结构、区域劳动力结构与资本结构改善对技术进步率的贡献作用。于是式(1)可以改写成：
Yt＝UtbKtαLtβ (2)
式(2)中，Ut＝((Et/Et-1))×(Ft/Ft-1))，其涵义在于资本生产率和劳动生产率的综合指数定义为资本生产率指数与劳动生产率指数之乘积。E表示资本生产率，(Et/Et-1)则为资本生产率指数。F表示劳动生产率，Ft/Ft-1)则为劳动生产率指数。其中，E＝Y/K，即资本生产率。F＝Y/L，即劳动生产率。
由式(2)对时间求导数可得：
(3)令
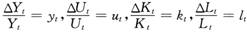，则式(3)可变形为：yt＝but+αkt+βlt (4)
式(4)表明，经济增长yt由资本增长贡献αkt、劳动力增长贡献βlt和效率体现式技术进步指数贡献but等3个部分组成。
(二)第二层次分解模型：基于要素质量和效率的技术进步贡献细分
总体技术进步既包括生产技术进步，也包括管理技术进步。基于生产技术进步包括资本装备率提高、劳动力劳动技能提升两个方面，是技术进步中最具决定性效用的主要因素，或者是技术进步诸因素的主要方面。经济增长中最具决定作用的技术进步因素在于资本有机构成，即由资本的技术构成决定并反映技术构成变化的资本价值构成，其中设备资本占比至关重要。劳动力劳动技能在机器设备的应用中非常重要，机器设备巨大效能的发挥都离不开人的操作和控制，假如劳动力素质和技能底下，那么，即使机器设备再先进也发挥不了多大的作用，也无法推动经济增长。与此同时，管理技术在经济增长中也至关重要，它是推动生产技术进步从潜在变成现实过程中必不可少的重要工具。因此不宜将总体技术进步对经济增长的贡献全部归属于生产技术进步，应当把效率体现式技术进步贡献but分解成生产技术质量贡献、生产技术效率贡献、劳动力空间构成贡献和其他管理技术进步贡献。
假定效率体现式技术进步指数函数为：
Atη＝DtEtγFtκHtπPtνStθ (5)
式(5)中，At为第t期的效率体现式技术进步指数，Dt为其他管理技术指数，Et为设备性资本占比，Ft为高技能劳动力占比，Ht为生产性技术进步效率指数，Pt为第二产业劳动力占比，St为第三产业劳动力占比。γ为设备性资本占比的产出弹性，κ为高技能劳动力占比的产出弹性，π为生产技术进步效率指数的产出弹性，ν为第二产业劳动力占比的产出弹性，θ为第三产业劳动力占比的产出弹性。其中，设备性资本占比＝设备性资本总量/固定资本总量，高学历劳动力占比＝高学历劳动力人数/劳动力总人数。生产技术进步效率指数＝设备性资本生产率×高技能劳动生产率，设备性资本生产率＝ GDP/设备性资本，高技能劳动生产率＝GDP/高学历劳动力。第二产业劳动力占比＝第二产业劳动力人数/劳动力总人数，第三产业劳动力占比＝第三产业劳动力人数/劳动力总人数。
由式(5)对时间求导数可得：
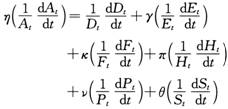(6)将式(6)的各项用年提升率代替(Δt＝1)，得：
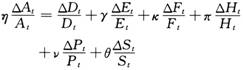(7)令
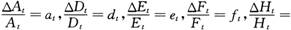
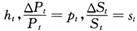，其中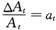
为效率体现式技术进步贡献，
为其他管理技术进步贡献。而ηat＝but，则式(7)变形为：but＝dt+γet+κft+πht+νpt+θst (8)
从式(8)还可以直接得到计算生产技术质量贡献、生产技术效率贡献、产业间劳动力构成贡献、其他管理技术进步贡献的归类测量公式。
生产技术质量贡献y1t：
y1t＝γet+κft (9)
生产技术效率贡献y2t：
y2t＝πht (10)
产业间劳动力构成贡献y3t：
y3t＝νpt+θst (11)
其他管理技术进步贡献y4t(即dt)：
y4t＝but-γet-κft-πht-νpt-θst (12)
三、实证数据描述
(一)产出增长率数据
《中国统计年鉴2011》提供了中国1978—2010年的不变价国内生产总值(其中1978—1980年为1970年不变价，1980—1990年为1980年不变价，1990—2000年为1990年不变价，2000—2005年为2000年不变价，2005—2009年为2005年不变价)。根据这些数据，可以计算出中国1980—2009年以1980年价格计算的国内生产总值即Yt序列数据，同时依据2010年比2009年的增长率又可以计算出2010年以1980年价格计算的国内生产总值，进而计算出中国1980—2010年以1980年价格计算的国内生产总值增长率(上年＝100)即yt序列数据。
(二)资本投入规模增长率和资本生产率数据
在技术进步贡献率计量文献中，对于其中的重要因子——资本投入量有6种观点：一是投资统计中的固定资产投资额，二是改革开放前物质生产部门的国民收入经过初次分配和再分配形成的积累额，三是各部门的固定资产原值(或净值)和流动资产平均余额，四是国民经济核算中的资本形成存量净额或固定资本形成存量净额，五是资本服务量，六是直接使用固定资本形成流量或资本形成流量来反映资本投入。
笔者认为，在进行经济增长分解计量中资本投入规模的统计口径应该选择固定资本总量，主要理由是：由于固定资本尤其是设备性资本才是人手的延长和人脑的扩展，它在社会扩大再生产中可以在较大程度上替代劳动力，随着资本装备水平的持续提高，可以持续推动劳动生产率的显著提高，因而只有固定资本投入才能对经济增长真正起到推动作用。尽管流动资本会对经济增长起到一定的影响作用，但这只是表现为流动资本短缺对经济增长的制约作用，而流动资本再充裕也不会对经济增长起到任何的推动作用。
本文根据普遍采用的永续盘存法来估算固定资本存量投入，测算公式为：
Kt＝(1-ν)Kt-1+ΔKt (13)
式(13)中，Kt表示第t年期末的固定资本投入总量，Kt-1表示t-1期末的固定资本存量，ν表示固定资本经济折旧率，ΔKt表示第t年度新增的固定资本数量。
本文采用固定资本形成总额作为新增固定资本的估算值，折旧率的估算参考张军等人的处理方法，取固定资本经济折旧率为9.6%。[12]
国家统计局国民经济核算司编写的《中国国内生产总值核算历史资料：1952—2004》公布了1953—2004年中国固定资本形成总额发展速度，《中国统计年鉴2011》公布了1978—2010年以当年价格计算的固定资本形成总额。张军等人[12]的研究已得出中国1952年固定资本存量为807亿元。因此，可以计算出1953—2010年以1952年价格计算的中国固定资本形成总额。再根据1980年以当年价格计算的固定资本形成总额与以1952年价格计算的固定资本形成总额之比，可以计算出1980—2010年以1980年价格计算的中国固定资本形成总额。据此，可由式(13)逐次计算出中国1978—2004年以1980年价格计算的固定资本投入Kt序列数据。
(三)劳动力投入规模增长率和劳动生产率数据
在技术进步贡献率计量文献中，对于其中的重要因子——劳动投入量有3种观点，一是大多数研究者选用劳动力人数作为劳动投入量。二是少量研究者认为劳动投入量既有劳动数量相关，也与劳动质量有关，而劳动质量因劳动者素质的高低会有很大的不同，因而选用总劳动时间作为劳动投入量。如日本文部科技省在计算日本的综合要素生产率时，通过国势调查形成的各产业从业人员劳动时间计算出全社会从业人员平均劳动时间，作为劳动投入的变量。三是还有研究者从既反映劳动数量又反映劳动质量的价值量角度，认为应当选用劳动者报酬作为劳动投入量。
笔者支持第一种观点，即选用劳动力投入人数作为劳动投入量。这是因为，在技术进步贡献率计量模型中，劳动投入增长贡献率是指劳动力投入规模扩大对经济增长所起到的贡献作用程度，劳动力人数则是劳动力投入规模的最好反映。然而，无论是将总劳动时间作为劳动投入量，还是将劳动者报酬作为劳动投入量，其共同论据是“劳动投入包括劳动数量和劳动质量”，其中的劳动质量是什么？“总劳动时间作为劳动投入量”论者的“劳动质量”为劳动力素质，而劳动力素质无非包括劳动者的劳动技能及其发挥程度，劳动技能提高明显属于生产技术进步；劳动技能的发挥程度则与劳动力资源配置、分配制度等诸因素高度相关，这属于管理技术问题。
劳动力投入规模增长率和劳动生产率中的劳动力投入采用就业人员总人数，数据源于《中国统计年鉴2011》公布的1952—2010年的中国就业人员总人数。根据这些就业人员总人数和上述19802010年以当年价格计算的中国国内生产总值数据，可以计算出1980—2010年的劳动力投入规模增长率lt序列数据和以当年价格计算的中国劳动生产率Ft序列数据，进而计算出1980—2010年以当年价格计算的中国劳动生产率提高率ft序列数据。
(四)设备性资本占比数据
基于中国官方公布的历年固定资本形成总额中没有划分出设备性资本形成总额，但是《中国统计年鉴2011》公布了1981—2010年的中国固定资产投资总额中划分出设备性固定资产投资，因此，本文采用1981—2010年的固定资产投资总额、设备性固定资产投资数据来估计各年度的设备性资本占比及其提高率。
(五)高技能劳动力占比数据
本文采用学历程度来反映劳动力的技能水平，以劳动力投入总量中学历在高中及其以上的那部分劳动力所占比重来表现和衡量高技能劳动力占比。其数据来源于《中国统计年鉴2011》。
(六)第二产业劳动力占比和第三产业劳动力占比数据
《中国统计年鉴2011》公布了1952—2010年的中国就业人员总人数以及第一产业、第二产业、第三产业的就业人员数量及其占比。根据这些数据，可以直接计算1980—2010年的中国第二产业劳动力占比提高率和第三产业劳动力占比提高率。
四、计量结果与分析
首先，按照式(4)进行最小二乘估计，回归分析采用Eview6.0软件完成。回归结果为：
yt＝0.001+0.516ut+0.487kt+0.456lt
调整后的可决系数R2高达0.999 4，表明模型拟合优度极佳，各回归系数都能通过1%的显著性检验。将α＝0.487，β＝0.456，u＝0.516代入式(4)，并利用表1的数据，则可以分解出1981—2010年各个年度、各个“五年计划”的资本规模、劳动力规模和技术进步对经济增长的贡献水平。每一时期的资本规模贡献度、劳动力规模贡献度、技术进步贡献度相加之和则是解释率，本模型对中国1981—2010年的平均解释率为98.682%，年度解释率在96.091%～99.724%之间，解释率的标准差系数只有0.832%，这表明了本文研究方法和结果的合理性与可靠性。
其次，按照式(8)，利用利用表1的数据和上面分解出的各年份技术进步贡献数据进行最小二乘估计，回归分析采用Eview6.0软件完成。回归结果为：
at＝0.001+0.542et+
调整后的可决系数R2高达1.000，表明模型拟合优度极佳，各回归系数都能通过1%的显著性检验。将γ＝0.542，к＝0.514，π＝0.529，ν＝0.004，θ＝-0.010代入式(8)，并利用表1的数据，则可以分解出1981-2010年各个年度、各个“五年计划”的生产技术质量、生产技术效率、产业间劳动力构成和其他管理技术进步对经济增长的贡献水平。
最后，利用上述分解结果的各解释变量对经济增长的贡献数据，则可以计算出资本规模、劳动力规模和技术进步对经济增长的贡献百分比，以及对技术进步贡献中生产技术质量、生产技术效率、产业间劳动力构成和其他管理技术进步对经济增长的贡献百分比(见表1)。
表1 1981—2010年经济增长贡献度分解表(按五年计划分)(%)
| 时间 | 资本规模贡献度 | 劳动规模贡献度 | 技术进步贡献度 | 其中 | |||
| 生产技术质量贡献度 | 生产技术效率贡献度 | 产业间劳动力构成贡献度 | 其他管理技术进步贡献度 | ||||
| 六五 | 38.662 | 14.151 | 44.888 | 18.371 | 26.766 | -0.405 | 0.157 |
| 七五 | 61.717 | 31.085 | 2.734 | -9.617 | 12.980 | -0.238 | -0.391 |
| 八五 | 43.812 | 3.737 | 52.005 | 3.807 | 48.790 | -0.469 | -0.123 |
| 九五 | 66.352 | 6.102 | 26.147 | 8.255 | 17.905 | -0.270 | 0.257 |
| 十五 | 61.425 | 3.279 | 34.397 | 19.869 | 14.278 | -0.245 | 0.495 |
| 十一五 | 63.951 | 1.579 | 33.938 | 25.900 | 7.737 | -0.059 | 0.360 |
| 30年 | 55.004 | 8.947 | 34.136 | 11.784 | 22.376 | -0.286 | 0.263 |
从上述计算结果的一系列数据中发现：
1.经济增长主要源于资本投入规模扩大。从1981—2010年30年间各个年度、各个“五年计划”经济增长中资本投入规模贡献、劳动力投入规模贡献、技术进步贡献的分解结果看，30年年均资本投入规模扩大1%可以带来经济增长0.487%，平均每年的资本投入规模贡献度达55%。其中有23个年度占第一位，并且大多数年份贡献占大头，1994—2010年中每年的贡献度均在51%以上，最高的年份达92%。6个“五年计划”中，资本投入贡献除“六五”占39%、“八五”占44%低于技术进步贡献外，其余4个“五年计划”均占60%以上，远远高于技术进步贡献。
2.劳动力投入规模对经济增长的贡献不大。从1981—2010年的30年间各个年度、各个“五年计划”经济增长中劳动力投入规模贡献的分解结果看，30年年均资本投入规模扩大1%可以带来经济增长0.456%，但是，由于劳动力投入规模增长不快，因而其对经济增长的贡献较小。30年中平均每年的劳动力投入规模贡献度只有9%。其中除1990年劳动力爆发性增长而造成其贡献非正常性巨大外，其余29个年度贡献度均在30%以下，1991—2010年每个年度贡献度均在7%以下，且呈下降趋势，2006—2010年每个年度贡献度均不到2%。
3.技术进步对经济增长的贡献较大。从1981—2010年30年间各个年度、各个“五年计划”经济增长中技术进步贡献的分解结果看，30年总平均每个年度的技术进步贡献度为34%。6个“五年计划”中，除第七个“五年计划”(1986—1990年)年均贡献度3%外，其余5个“五年计划”年均贡献度在26%～52%之间。第七个“五年计划”年均贡献度较低的表象原因是资本生产率大幅下降，而劳动生产率却提升不大，其中1990年资本生产率和劳动生产率出现了双降，尤其是1990年劳动力人数比上年末大增17%，GDP只增长了4%，以致劳动生产率下降了11%。从深层次原因剖析，则在于国家全面实施了偿还历史欠账式的就业政策，1990年增加的就业人口9 420万人中，第一产业增加5 690万人，占60%。第二产业增加1 880万人，占20%。第三产业增加1 850万人，占20%。增加在第一产业的劳动力中绝大部分属于“被就业”。从而，导致这一年的三大产业劳动生产率全面大降，其中第一产业劳动生产率下降4%，第二产业劳动生产率下降13%，第三产业劳动生产率下降14%。资本生产率处于持续下滑趋势，30年中除了1982—1985年、1987年、1991—1993年共8个年度提升外，其余22年均表现为不同程度的下降，尤其是1994年开始至2010年出现了持续性的连年明显下滑。引致1994—2010年资本生产率持续性的连年明显下降的原因有四：一是替代劳动性的设备性资本领先增长，二是匹配设备性的建筑物投入较快增长，三是重复建设造成的产能严重过剩，四是非生产性基本建设投资连年过快增长。
4.技术进步对经济增长的贡献主要源于生产技术质量和生产技术效率提升。从1981—2010年30年间各个年度、各个“五年计划”技术进步对经济增长的贡献中生产技术质量贡献、生产技术效率贡献、产业间劳动力构成贡献和其他管理技术进步贡献的分解结果看，30年年均经济增长率中由生产技术质量提升带来的经济增长份额占12%，由生产技术效率提升带来的经济增长份额占22%，这两种合计为34%，占技术进步贡献总份额的100%。从6个“五年计划”考察，生产技术质量、生产技术效率对经济增长的贡献度运动变化均表现为强波动性。生产技术质量贡献度的标准差高达12%，标准差系数高达106%，其贡献度在“六五”时期年均18%，“七五”下降了-10%，“八五”至“十一五”时期表现为逐期快速提升态势，从“八五”的年均递增4%到“十一五”的年均递增26%，即“十一五”时期年均贡献度比“七五”时期提升了36个百分点。生产技术效率贡献度的标准差高达14%，标准差系数高达63%，其贡献度“八五”时期最高，年均为49%，“十一五”时期最低，年均为8%，这两者之间相差41个百分点，前者是后者的6倍。
5.设备性资本占比对经济增长的贡献作用差强人意。从理论上讲，设备性资本是提升技术装备水平，增强设备替代劳动力能力，提高劳动生产率的根本性要素，是促进经济增长的有效路径之一。通过对中国1981—2010年经济增长有关数据的回归分析，发现设备性资本占比对经济增长的产出弹性高达0.542，也就是说设备性资本占比每提高1%就可以实现经济增长0.542%，这有力地佐证了提高设备性资本占比对经济增长的较大拉动作用。然而，令人困惑的是，同样是对1981—2010年经济增长有关数据的回归分析结果表明，设备性资本占比在中国经济增长中却远远没有起到应有的贡献作用，贡献度年均只有0.192%。在30年中除了1981—1988年、2005年共9个年度为正贡献外，其余21个年度均为负贡献。在6个“五年计划”中除了“六五”时期年均贡献度为13.862%、“七五”时期年均贡献度为1.252%外，“七五”至“十一五”共4个“五年计划”时期的贡献度均为负数。2010年与1980年比较，历经30年后的设备性资本占比年均只提升0.021%，对经济增长的贡献度年均只有0.011%。设备性资本占比提升缓慢，2010年设备性资本占比23%，比1980年提升0.162个百分点，年均只提升0.023个百分点。其中，1981—1988年呈现连年提升趋势，从1980年的23%一直提高到1988年的27%，8个年度共提高了4个百分点，这是该一时期国家实施全面推进技术更新和改造政策的良好结果。1989—2010年的22年中除了2005年度有所提升外，其余21个年度持续不断下降，从1988年的27%一直下滑到2010年的23%，总共下降了4个百分点，这是该一时期外延式扩大再生产和劳动密集型扩大再生产盛行、基础设施和住宅建设等非生产性投资过快增长的综合反映。在住宅投资方面，据国家统计局公布的1995—2010年统计数据测算，全国住宅投资年均递增16%，比全部固定资产投资增速高3个百分点。
6.高技能劳动力占比对经济增长的贡献作用较大。通过对中国1981—2010年经济增长有关数据的回归分析，发现高技能劳动力占比对经济增长的产出弹性高达0.514，也就是说高技能劳动力占比每提高1%就可以实现经济增长0.514%，揭示了提高高技能劳动力占比对经济增长具有较大的拉动作用。同时，对1981—2010年经济增长有关数据的回归分析结果还表明，高技能劳动力占比在中国经济增长中确实起到了较大的贡献作用，贡献度年均12%。在30年中除了1984年、1985年、1990年共3个年度为负贡献外，其余27个年度均为正贡献，并且有18个年份的贡献度为两位数；在6个“五年计划”中除了“七五”时期年均贡献度为-11%外，“六五”、“八五”至“十一五”共5个“五年计划”的贡献度均为正数，其中“十一五”时期的贡献度最高，达28%。2010年与1980年比较，历经30年后的高技能劳动力占比年均提升了2%，对经济增长的贡献度年均12%。高技能劳动力占比提升较快，这应当归功于高等教育的高速发展。尽管近几年来中国高等教育发展中存在这样那样问题，但是，高等教育高速发展对经济增长的积极支撑和推动作用之主流是不容否定的。
7.生产技术效率对经济增长的贡献作用显著。通过对中国1981—2010年经济增长有关数据的回归分析，发现生产技术效率对经济增长的产出弹性高达0.529，也就是说生产技术效率每提高1%就可以实现经济增长0.529%，揭示了提高生产技术效率对经济增长具有较大的推动作用。同时，对1981—2010年经济增长有关数据的回归分析结果还表明，生产技术效率在中国经济增长中确实起到了较大的贡献作用，贡献度23%。在30年中除了1981年、1989年、1990年、2008年共4个年度为负贡献外，其余26个年度均为正贡献，并且有20个年份的贡献度为两位数。6个“五年计划”时期年均贡献度均为正数，其中“八五”时期的年均贡献度最高，达49%。2010年与1980年比较，历经30年后的生产技术效率年均提升了2%，其中除了1981年、1989年、1990年、2008年共4个年度为下降外，其余26个年度呈现出较强的持续提高轨迹。其原因在于：一是生产工具和生产工艺的配置与利用能力连年增强，生产工具的有效利用率持续提升；二是劳动力配置、管理和利用能力不断增强，劳动效率持续提升。
8.产业间劳动力结构对经济增长的贡献作用微弱。通常人们以为，产业间劳动力结构对经济增长的贡献作用较大，然而，通过对中国1981—2010年经济增长有关数据的回归分析结果却表明，产业间劳动力结构对经济增长的产出弹性却很弱小，第二产业劳动力占比对经济增长的产出弹性只有0.004，第三产业劳动力占比对经济增长的产出弹性为-0.010，揭示了产业间劳动力结构对经济增长的拉动作用微乎其微。同时，对1981—2010年经济增长有关数据的回归分析结果还表明，产业间劳动力结构在中国经济增长中所起到的贡献作用确实可以忽略不计。在30年中，产业间劳动力结构调整贡献度有28年为负数，两年为正数。正贡献的两年为1982年和2007年，贡献度依次为0.151%，0.123%。其余27年为负贡献，其中负贡献度最大的1986年为0.151%，次之的1984年为0.732%。2010年与1980年比较，历经30年后的产业间劳动力结构调整对经济增长的贡献度年均-0.291%。在6个“五年计划”时期中，产业间劳动力结构调整的年均贡献度每个“六五”时期均为负数，“六五”时期年均贡献度为-0.404%，“七五”时期负贡献度缩小到0.245%，“八五”恶化为-0.473%，随后逐个“五年”时期好转，从“九五”的年均-0.271%到“十五”的年均-0.245%，再到“十一五”的-0.062%。由此可见，1981—2010年的产业间劳动力结构调整对经济增长的贡献无论是30年总体维度讲，还是从这30年中的每一个年度说，其贡献度都是十分微小的。
五、研究结论
本文构建出双层经济增长分解模型，利用中国1980—2010年的时间序列数据，引入资本生产率与劳动生产率的综合指数来体现总体技术进步水平，从而使总体技术进步贡献的直接计量成为可能，并且实现了资本和劳动力的规模与质量、速度与效率在对经济增长贡献作用中的逻辑关系得以全面完整体现；引入生产技术质量(设备性资本占比和高技能劳动力占比)、生产技术效率、劳动力空间构成等因子，对总体技术进步对经济增长贡献构建分解模型进行深入分解，可以解释各种类型、各种方式的技术进步对经济增长的贡献程度。实证研究结果表明：(1)经济增长主要源于资本投入规模扩大，资本投入规模扩大1%可以带来经济增长0.487%，资本投入规模贡献度达55%。劳动力投入规模对经济增长的贡献不大，资本投入规模扩大1%可以带来经济增长0.456%，但劳动力投入规模贡献度只有9%。总体技术进步对经济增长的贡献较大，其对经济增长的贡献度34%。(2)技术进步对经济增长的贡献主要源于生产技术质量和生产技术效率提升，由生产技术质量提升带来的经济增长份额占12%，由生产技术效率提升带来的经济增长份额占22%，而产业间劳动力结构对经济增长的贡献作用微乎其微，第二产业劳动力占比对经济增长的产出弹性只有0.004，第三产业劳动力占比对经济增长的产出弹性为-0.010。(3)设备性资本占比对经济增长的产出弹性高达0.542，也就是说设备性资本占比每提高1%就可以实现经济增长0.542%，这有力地佐证了提高设备性资本占比对经济增长的较大拉动作用，但其对经济增长的贡献度年均只有0.192%，其原因在于设备性资本占比除1981—1988年、2005年提升外，1989—2010年中的21个年度持续不断下降。(4)高技能劳动力占比对经济增长的贡献作用较大，其对经济增长的产出弹性高达0.514，也就是说高技能劳动力占比每提高1%就可以实现经济增长0.514%，对经济增长的贡献度年均12%。(5)生产技术效率对经济增长的贡献作用显著，其对经济增长的产出弹性高达0.529，也就是说生产技术效率每提高1%就可以实现经济增长0.529%，对经济增长的贡献度年度高达23%，并且呈现较强的持续提高趋势。生产技术效率对经济增长的贡献作用持续提升的运动轨迹表明，中国设备性资本配置管理的科学性和利用的有效性水平都在持续提高，劳动力尤其是高技能劳动力的配置使用科学合理性和劳动努力程度也在持续提升。
参考文献
[1]R. Solow. Technical Change and the Aggregate Production Function [J]. Review of Economics and Statistics, 1957,39(3).
[2]曹吉云.我国总量生产函数与技术进步贡献率[J].数量经济技术经济研究，2007，(11).
[3]易纲，樊纲，李岩.关于中国经济增长与全要素生产率的理论思考[J].经济研究，2000，(8).
[4]华冬芳，李智勇.改革开放以来中国全要素生产率变动的估算[J].商业时代，1998，(28).
[5]徐瑛，陈秀山，刘凤良.中国技术进步贡献率的度量与分解[J].经济研究，2006，(8).
[6]熊俊.经济增长因素分析模型：对索洛模型的一个扩展[J].数量经济技术经济研究，2005，(8).
[7]陈瑾瑜.全要素生产率与技术进步间的差别及测算——几何微分法的应用[J].数量经济技术经济研究，2012，(6).
[8]宋冬林，王林辉，董直庆.资本体现式技术进步及其对经济增长的贡献率(1981—2007) [J].中国社会科学，2011，(2).
[9]孙克.中国资本体现式技术进步估计[J].经济科学，2011，(3).
[10]赵志耘，刘晓路，吕冰洋.中国要素产出弹性估计[J].经济理论与经济管理，2006，(6).
[11]辛永容，陈圻，肖俊哲.要素产出弹性与技术进步贡献率的测算[J].管理科学，2009，22(1).
[12]张军，吴桂英，张吉鹏.中国省际物质资本存量估算：1952—2006[J].经济研究，2004，(10).