四、真实数据分析
我们以2004-2008年我国各地区城镇居民人均可支配收入x(元)和消费支出y(元)的面板数据为例,利用上述提出的分位回归方法对近5年来我国城镇居民收入消费模式进行建模分析,探讨居民人均可支配收入x对其消费支出y的影响,数据来源于《中国统计年鉴(2005-2009)》。
通过对总体数据作散点图容易看到y与x之间有比较明显的线性关系,所以可以考虑采用线性模型来刻画。而通过横向散点图可以看到各地区y与x的斜率变化不大,但截距却有明显的不同,即各地区平均边际消费倾向差异不大,但自发消费存在着明显差异;从纵向散点图可以看到各年度y与x的关系基本相同,无论是斜率还是截距都没有发生太大变化,所以可以认为不存在时期效应。首先考虑直接利用混合数据建立简单线性模型:
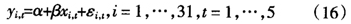
LS估计的结果如表6。
表6LS估计值及显著性检验
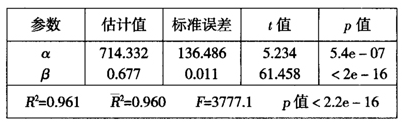
虽然从表6的结果来看,模型和参数都通过了显著性检验,可决系数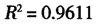 也比较高,但残差分析图显示方差并不相等,而且残差值波动比较大,拟合效果并不好,这有可能是由于LS估计没有照顾到各地区可能存在的个体差异而引起的。另外91号数据(广东省2008年)、92号数据(广东省2007年)和129号数据(西藏2005年)残差表现异常,这也使得上述β的LS估计
也比较高,但残差分析图显示方差并不相等,而且残差值波动比较大,拟合效果并不好,这有可能是由于LS估计没有照顾到各地区可能存在的个体差异而引起的。另外91号数据(广东省2008年)、92号数据(广东省2007年)和129号数据(西藏2005年)残差表现异常,这也使得上述β的LS估计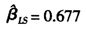 在这些异常点的强影响下可能错估了平均边际消费水平。
在这些异常点的强影响下可能错估了平均边际消费水平。
考虑带个体固定效应的模型:
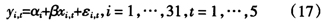
从第三节的蒙特卡洛模拟结果来看,当模型判断正确时,FE估计是能够极大地改进LS估计的,对参数β的估计也具有较高的精度和稳定性,所以我们首先用FE估计法对参数进行估计,结果如下:
表7FE估计值及显著性检验
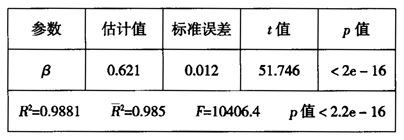
从表7结果来看,F值显著增加,模型的拟合优度也提高了很多(当然这也有部分原因是由于我们加入了新的解释变量而引起的)β的估计值也高度显著,残差分析图显示残差方差异常的情况消失了,而且残差呈现正态分布。诊断发现129号数据(西藏2005年)和130号数据(西藏2004年)异常,从实际数据来看,这与西藏这两年收入与支出太接近有关系,其2005年和2004年两者之间分别只相差814.07元和767.86,这都只有当年全国各地区平均相差值2422.6元和2126.38元的1/3,属于比较特殊的值。从上面综合来看,个体固定效应模型能更好地反映我们数据的内在关系,且FE估计值比LS估计值更为精确,从其对β的估计值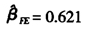 来看,显然LS估计
来看,显然LS估计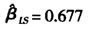 是高估了城镇居民的平均边际消费水平。
是高估了城镇居民的平均边际消费水平。
虽然从上述的各方面来看,我们有理由相信FE法给出了β较为合理的估计,但我们至少还必须注意到两点:一是西藏地区在2005年和2004年的数据出现异常,这仍将会对β的FE估计值造成一定影响,且由于我们并不清楚这两个异常值是由于数据的错误造成的还是其本身就是反映了真实情况,所以不能对其进行武断的删除并认为删除后的估计会更好;二是从收入与支出的散点图显示当收入增大时,样本点有发散的趋势,由于处于收入小于15000元的点过多过集中,使得我们的LS估计和FE估计在使残差平方和最小的准则下并没有完全照顾到收入较高的居民的真实消费意愿,所以有必要对数据做进一步的分析和考证。由于分位回归法对异常值并不敏感,而且它能利用分位点的变化给出各个层次消费支出与收入的变化情况,所以正好能够弥补上述LS估计和FE估计在这方面存在的不足。由于我们认为个体固定效应比较显著,所以接下来我们不考虑直接利用混合数据的普通分位回归方法,而直接给出本文提出的另外3种分位回归方法在τ=0.5时对居民平均边际消费倾向β的估计值:
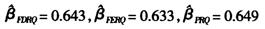
可以看到3种估计的结果比较接近,而且都比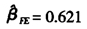 大但比
大但比 小。第三节蒙特卡洛模拟的结果比显示FEQR法在固定效应模型中对参数的估计精度和稳定性都是表现较好的,所以下面我们以FEQR法来分析不同消费水平居民的收入支出模式是否有所不同。
小。第三节蒙特卡洛模拟的结果比显示FEQR法在固定效应模型中对参数的估计精度和稳定性都是表现较好的,所以下面我们以FEQR法来分析不同消费水平居民的收入支出模式是否有所不同。
图1给出了边际消费倾向β随分位点τ变化而变化的函数图,我们发现,β值随着τ的变化呈现较大波动,当τ从0.02→0.10时,β值快速增加,而在T从0.10→0.77时,β值则缓慢平稳增加,直至达到最大值0.659,而之后则渐趋平稳并在τ≈0.90后快速下降,到τ=0.98时β值已降至为0.603。从图1中不难看到,边际消费倾向最高的是消费水平在0.6至0.9分位点之间的居民,即中高消费群体;
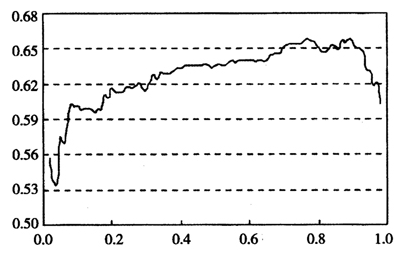
图1FEQR估计随分位点变化函数图 FEQR估计随分位点变化函数图最低的是0.2分位点以下的居民,即低消费群体,不过虽然他们的平均边际消费水平是最低的,但当他们收入增加时,其平均边际消费倾向增加的意愿却是最强烈的。另外对于0.9分位点以上的高消费居民,虽然他们的边际消费倾向不是最低的,但其收入的再增加并不会增加他们的边际消费倾向,反而是有明显的降低边际消费倾向的意愿。以上发现都是传统均值回归方法无法捕捉到的信息,但这些信息却为我们当前制定刺激消费的宏观经济政策提供了有利参考:即有效的刺激消费政策应该努力提高中低消费居民的收入水平。
参考文献:
[1]Koenker R. and Bassett G.. Regression Quantile[J]. Econometric a, 1978(46): 33-50.
[2]Koenker R. Quantile Regression for Longitudinal Data[J]. Journal of Multivariate Analysis, 2004(91): 74-89.
[3]Tian, Maozai. and Chen, Gemai. Hierarchical Linear Regression Models for Conditional Quantiles[J].Science in China, Series A: Mathematics, 2006, 49(12): 1830-1838.
[4]Galvao, A. F. Quantile Regression for Dynamic Panel Data[J].University of Illinois at Urbana-Champaign, Working Paper,2008.
[5]Galvao, A. F. and Montes-Rojas, G. V. Instrumental Variables Quantile Regression for Panel Data with Measurement Errors[J].University of Wisconsin-Milwaukee, Working Paper, 2009.
[6]Harding M. and Lamarche, C. A. Quantile Regression Approach for Estimating Panel Data Models Using Instrumental Variables[J].Ecanomics Letters, 2009(104): 133-135.
[7]Powell, D. Unconditional Quantile Regression for Panel Data with Exogenous or Endogenous Regressors[J]. RAND Corporation Publications Department in its series Working Papers, 2009.710.
经济学
面板数据的分位回归方法及其模拟研究(三)
http://www.newdu.com 2018/3/7 《统计研究》(京)2010年10期第81~87页 罗幼喜 田… 参加讨论
Tags:面板数据的分位回归方法及其模拟研究(三)
责任编辑:admin相关文章列表
没有相关文章
[ 查看全部 ] 网友评论
