内容提要:本文采用广义空间动态面板数据模型(GSDPD)和2002第一季度至2010年第三季度省际面板数据分析了我国房地产价格的区域互动。实证结果表明,我国房地产价格互动存在空间滞后效应和时间滞后效应,且城镇居民可支配收入、信贷扩张、土地价格和房屋竣工面积是影响我国房价的重要因素。实证结果还表明,相邻地区之间房价的影响程度比其他不相邻地区之间房价的影响程度大,经济特征相似地区间房价的相互影响程度比经济特征不相似地区间房价的相互影响程度小。
关键词:房地产价格,广义空间动态面板模型,SCAB估计,SCBB估计
作者简介:陈浪南,男,1958年生,福建人,中山大学经济研究所、岭南学院教授。研究方向为金融经济学、货币经济学。王鹤,男,1982年生,湖南省人,现为湖南科技大学商学院讲师。研究方向为金融经济学。
一、引言与文献回顾
一些学者主要关注单个城市层面或国家总体层面房价的影响因素。Bramley(1993)认为房地产价格是房地产供给、人口、经济因素和地理位置的函数。Green(1999)则从需求和供给两方面考查房地产价格的决定因素。Hwang和Quigley(2006)利用美国面板数据分析了收入、建筑成本和当地经济状况对房价的影响。梁云芳、高铁梅(2006)从需求、供给和资本的可获得性分析了我国住宅价格波动的成因。梁云芳、高铁梅(2007)基于误差修正模型讨论了房价区域波动差异的成因,得出信贷规模对东、西部地区的影响比较大,实际利率对各地区影响差异不大且影响较小的结论。严金海(2006)研究了房价与地价的关系。董志勇等(2010)从需求方、供给方、地方政府及贷币政策变量角度考察了房地产价格的影响因素。
另一些学者则关注房地产价格的区域互动关系。Meen(1996)和Wood(2003)探讨了房地产价格区域互动的产生机制:“波纹效应”理论及产生原因。MacDonald和Taylor(1993)、Alexander和Barrow(1994)、Munro和Tu(1996)应用协整技术检验了英国各地区房地产价格的趋同性。Wood(2003)、Gupta和Miller(2009)利用格兰杰因果检验分别检验了英国和美国房地产价格区域互动的成因。从区域维度考虑房地产价格互动关系丰富了对单一地区(城市)房价影响因素的研究,同时也推动了针对全国房价的研究向区域维度深入。格兰杰检验能较好地发现房价在各地区之间的传导机制,但格兰杰检验中无法引入影响房价的其他解释变量。空间计量模型的出现为解决此问题提供了分析工具。Clapp和Tirtiroglu(1994)最先将空间效应引入到房地产价格的动态分析中。Clapp和Tirtiroglu运用美国康涅狄格州哈特福德地区房地产市场数据发现,一个给定次级市场的房价不但受其滞后期价格影响,而且受相邻次级市场房价影响。Pollakowski和Ray(1997)在更高的加总水平上检验了房价的空间扩散效应。
近期,随着面板数据模型和空间计量模型的发展,许多关于房地产价格的文献都在空间动态面板数据的框架下进行。Loannides和Thanapisitikul(2008)利用美国375个都市区1975—2007年的调查数据,分别考查了美国房价的空间效应和时间效应,结果表明美国城市房价之间存在空间扩散效应和时间滞后效应。Brady(2011)在房价空间滞后模型中加入一个因变量的滞后一期项(Yt-1)来体现房地产价格的自相关,得到了反映房地产价格变动的空间动态面板模型,并利用OLS估计和IV估计对加利福尼亚州房价进行了实证分析。结果发现,因变量的空间滞后因子与时间滞后因子的回归系数都显著,即该地区房价之间存在空间扩散效应和时间滞后效应。Holly等(2011)在空间误差模型的基础上得到了房地产价格的时空模型,并利用美国经济部分析局调查的房价数据和美国房价州际面板数据研究了美国的房地产价格空间相关性。研究结果表明,美国房价存在空间自相关效应。根据其对空间相关的处理方式不同,以上文献可分为两类:一是将空间相关项放入主方程得空间自相关动态面数据模型(Brady(2011)),然后用OLS或IV估计法进行估计。由于内生性问题,这种处理方法会造成估计结果出现偏差。二是在干扰项中考虑空间相关,得到空间误差动态面板数据模型(Holly(2011)),将空间相关看成截面弱相关。但这种处理方式可能存在设定误差。
有关房地产价格区域相关性的研究,我国目前处于起步阶段,主要集中在各地区房价是否存在长期协整关系、“核心地区(城市)”房价与周边地区(城市)房价是否存在格兰杰关系。王松涛等(2008)应用Johansen协整关系检验、多变量格兰杰因果关系检验和脉冲响应函数方法,分别分析了我国5个主要区域市场城市房价之间的互动关系。黄飞雪等(2009)综合运用协整检验方法分析了自1999年1季度至2008年3季度间中国副省级以上城市房屋销售价格的关联性。钱金保(2008)采用空间误差修正模型进行了中国房地产价格的泡沫检验和空间联动分析。本文首次构建广义空间动态面板模型(GSDPD),并运用空间纠正差分GMM估计量与空间纠正系统GMM估计量进行估计。
二、广义空间动态面板数据模型
(一)模型设定
为了充分考虑我国房价的时间滞后效应和空间滞后效应,本文首先建立一个带有一阶滞后房价变量与空间滞后房价变量的广义空间动态面板数据模型(GSDPD)。模型设定如下:
Pt=λPt-1+δWnPt+Xtβ+ut
ut=ρMnut+εt (1)
式中,Pt为n×1向量,表示第t期n个地区的房价,Pt-1为房价的时间滞后项,Wn为n×n的空间加权矩阵,WnPt为空间滞后项,Xt为n×K矩阵,表示K个影响房价的其他因素在第t期的观测值,具体取值见数据部分,ut为n×1扰动向量,εt=INη+vt,vt~iid(0,σv
(二)估计方法
式(1)中既包含了因变量的时间滞后和空间滞后项(皆为内生变量),也包含了空间误差项(非球形扰动),本文采用空间纠正差分GMM估计量(SCAB)与空间纠正系统GMM估计量(SCBB)进行估计。
1.空间纠正差分GMM估计量。空间纠正差分GMM估计量(SCAB)是将Arellano和Bond(1991)考虑的动态面板数据模型扩展到包括空间自相关项和空间误差项的情形,具体分三步实现:
第一步,解决空间滞后项和时间滞后项带来的内生性问题,通过GMM估计θ,并利用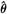
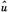 t=Pt-zt
t=Pt-zt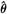 ,其中zt≡[Pt-1,WNPt,Xt]表示解释变量矩阵,θ≡[λ,δ,β']'为一个包含K+2个参数的列向量。为了从εt消除个体效应η,首先对式(1)取一阶差分得:
,其中zt≡[Pt-1,WNPt,Xt]表示解释变量矩阵,θ≡[λ,δ,β']'为一个包含K+2个参数的列向量。为了从εt消除个体效应η,首先对式(1)取一阶差分得:
ΔPt=Δztθ+Δut t=3,…,T (2)
ΔUt=(IN-ρMn)-1Δvt
根据Arellano和Bond(1991)、Kelejian和Robinson(1993)及Jacobs和Ligthart(2009),取因变量的水平值(yt-2,…,y1)、WNΔXt和外生变量的一阶差分作为工具变量。工具变量矩阵HSAB(t)①可定义为
HSAB(t)=[yt-2,…,y1,WNΔXt,ΔXt] (3)
HSAB由HSAB(t)按时间累加而成。我们可以得到空间差分GMM估计量(SAB):
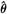 SAB=[Δz'HSABASABH'SABΔz]-1Δz'HSABASABH'SABΔP (4)
SAB=[Δz'HSABASABH'SABΔz]-1Δz'HSABASABH'SABΔP (4)
其中ASAB=[H'SABGsHSAB]-1为一个F×F矩阵,Cs=IN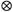 G是一个n(T-2)×n(T-2)的加权矩阵,G中的元素为:
G是一个n(T-2)×n(T-2)的加权矩阵,G中的元素为:
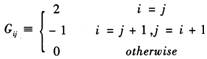 (5)
(5)
第二步,得到ρ和σv2的一致估计量。ρ和σv2的一致估计量由Kapoor等(2007)提出的矩条件修改得。记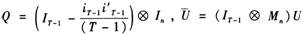 ,可得到3个恒等式作为总体矩条件:
,可得到3个恒等式作为总体矩条件:
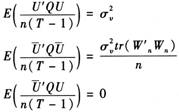 (6)
(6)
基于第一步得到的广义残差,可形成上述总体矩条件的样本矩,再由NLS可以得到ρ以及σV2的一致估计。
第三步,解决非球形扰动带来的问题,得到模型中参数的有效估计。类似于扰动项时间自相关情形下的解决方案,本部分采用空间FGLS方法(具体操作是对所有变量(记为y)进行Cochrane-Orcut-type变换: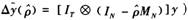 ,对变换后的数据再次进行第一步估计得空间纠正差分GMM估计量(SCAB):
,对变换后的数据再次进行第一步估计得空间纠正差分GMM估计量(SCAB):
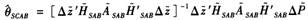 (7)
(7)
式中,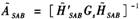 ,而
,而 SAB中的元素为
SAB中的元素为 SAB(t)=[IN-
SAB(t)=[IN-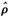 MN]HSAB(t)。
MN]HSAB(t)。
2.空间纠正系统GMM估计量。将Blundell和Bond(1998)考虑的动态面板数据模型扩展到包括空间自相关项和空间误差项的情形,得到:
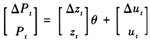 (8)
(8)
为了表示方便,将式(8)写成:
PBB(t)=zBB(t)θ+uBB(t) (9)
与空间纠正差分GMM估计量(SCAB)类似,空间纠正系统GMM估计量(SCBB)分三步实现:
第一步,得到空间系统GMM估计量(SBB):
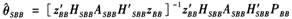 (10)
(10)
式中,ASBB=[H'SBBGSBBHSBB]-1,且HSBB和GSBB分别定义为:
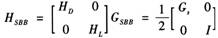 (11)
(11)
HD为一阶差分方程的工具变量矩阵,HL为水平方程的工具变量矩阵,Cs取值与前面一样,I为单位矩阵。
第二步,类似于上面方法,将第一步得到的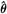 SBB代入
SBB代入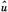 =P-z
=P-z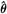 SBB,此时z只包含变量的水平值,然后利用矩条件,得到ρ和σv2的一致估计量。
SBB,此时z只包含变量的水平值,然后利用矩条件,得到ρ和σv2的一致估计量。
第三步,利用
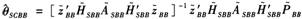 (12)
(12)
式中,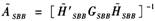 ,而
,而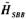 中的元素为
中的元素为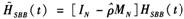 。
。
三、权重矩阵与样本数据
(一)空间权重矩阵的选取
空间权重矩阵w表征了空间单位之间的相互信赖性与关联程度。实证研究中,通常采用相邻规则与距离规则来定义空间加权矩阵。为了研究需要,本文从地理位置特征与社会经济特征两个不同角度分别建立包括相邻规则与距离规则的空间加权矩阵,以便更准确地把握房价的区域相关关系。
1.地理位置特征加权矩阵。本文采用两种常用的地理位置特征矩阵体现房价的空间相关关系:第一种是空间相邻加权矩阵W1,其中的元素wi,j=1表示两个地区拥有共同的边界,wi,j=0表示两个地区没有共同的边界,然后对矩阵进行标准化处理。为了避免“单个岛屿效应”,设定海南省与广东省、广西壮族自治区有共同边界。第二种是空间距离加权矩阵W2,其元素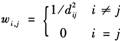 ,即两地区之间距离越远,相互之间的影响程度越小,两地区之间的距离di,j为两地区省会城市之间的距离②。
,即两地区之间距离越远,相互之间的影响程度越小,两地区之间的距离di,j为两地区省会城市之间的距离②。
2.社会经济特征加权矩阵。以地理区位差异反映出区域房价的空间联系体现了地理位置特征的影响,但区域房价的空间联系可能会受经济发展水平等其他因素的影响,因此本部分进一步建立空间经济加权矩阵。具体为,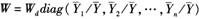 ,其中为样
,其中为样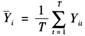 本期内第i个省份实际人均GDP的平均值,
本期内第i个省份实际人均GDP的平均值,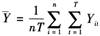 为样本期内实际人均GDP的总平均值,当Wd=W1时,得经济相邻加权矩阵W3,当Wd=W2时,得经济距离加权矩阵W4。通过空间经济加权矩阵可以发现,当一个地区实际人均GDP比较大时(即
为样本期内实际人均GDP的总平均值,当Wd=W1时,得经济相邻加权矩阵W3,当Wd=W2时,得经济距离加权矩阵W4。通过空间经济加权矩阵可以发现,当一个地区实际人均GDP比较大时(即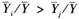 ),对其周边地区的影响也较大(wi,j>wj,i)。
),对其周边地区的影响也较大(wi,j>wj,i)。
(二)变量与数据
本文采用我国2002年第一季度至2010年第三季度的省际面板数据。数据主要来源于中国经济信息网经济统计数据库。由于许多数据缺失,西藏未包含在内。主要变量包括商品房销售额、商品房销售面积、城镇居民实际人均可支配收入、房屋竣工面积、土地购置费、土地购置面积、房地产投资资金来源、房地产投资资金来源中自筹资金。因变量商品房平均销售价格由商品房销售额除以商品房销售面积得到,自变量中土地价格由土地购置费除以土地购置面积得到,信贷扩张指标由房地产投资资金来源减去自筹资金得到③。
四、实证结果与分析
当式(1)中不考虑干扰项的空间相关时(ρ=0),可利用SAB和SBB估计模型。表1为在空间相邻加权矩阵下,我国区域房价空间自相关动态面板数据模型的SAB、SBB、OLS和LSDV估计结果。
表1 我国房价的SAB、SBB、OLS、LSDV估计结果
|
|
OLS估计 |
SAB估计 |
SBB估计 |
LSDV估计 |
|
房价的 一期滞后 |
0.672*** (24.66) |
0.587*** (15.88) |
0.540*** (18.63) |
0.589*** (23.02) |
|
房价的 空间滞后 |
0.183*** (8.56) |
0.176*** (8.57) |
0.161*** (12.36) |
0.118*** (4.93) |
注:①SAB估计和SBB估计中第一步使用的都是两阶段GMM估计且使用了Windmeijer(2005)提出的方法对两阶段方差矩阵进行有限样本调整,***、**、*分别表示1%、5%、10%的显著性水平,括号中的数值为t值。②在回归过程,我们考虑了体现季节趋势的虚拟变量,由于大部分回归结果中,季节趋势表明不显著,从而回归结果中未列出。③由于篇幅问题此处只列出了房价空间滞后项与时间滞后项的估计结果。
由表1可知,由OLS估计、LSDV估计、SAB估计和SBB估计得到的房价空间滞后项和房价一期滞后项回归系数的估计值皆为正数,且都在1%的水平下显著。这表明,在研究我国房价时,考虑其时间滞后效应与空间滞后效应是必要的。但进一步观察发现,房价一期滞后项回归系数的SAB估计值(0.587)和SBB估计值(0.540)比LSDV估计值(0.589)小,出现了低估问题④,这可能是因为未考虑干扰项的空间相关造成的,因此,本文进一步通过SCAB、SCBB估计我国区域房价广义空间动态面板数据模型,结果见表2。
由表2可知:
(1)在考虑了扰动项的空间自相关后,由OLS估计、LSDV估计、SCAB估计和SCBB估计得到的房价一期滞后项和空间滞后项系数的估计值依然为正数,且都在1%的水平下显著。这表明,我国房地产价格存在空间与时间滞后效应。
(2)比较房价一期滞后项的四个估计值发现,SCAB估计值(0.569)和SCBB估计值(0.572)介于OLS估计值(0.668)与LSDV估计值(0.567)之间。这说明,使用广义空间动态面板数据模型来分析我国房价是合适的。Jacobs和Ligthart(2011)发现SCBB估计比SCAB估计有更好的小样本性质,从而在分析我国房地产价格的区域互动关系时使用SCBB估计法更优。Blundell和Bond(1998)在进行系统GMM估计时,要求模型中的异质扰动项vit不存在序列相关。表2中SCBB估计的AR(1)检验结果显著,AR(2)检验结果不显著⑤,表明本模型中的异质扰动项vit满足序列不相关的要求。根据Roodman(2006,2009)研究⑥,本文在进行SCBB估计时,内生变量的工具变量都是使用工具变量的“collapsing”形式⑦,且Hansen检验结果表明模型中不存在过度识别问题。因此,本文的AR(1)、AR(2)、Hansen检验结果都表明SCBB估计法的使用是恰当的。
(未完待续)
责任编辑:夏雨
