中国工业结构变化与技术进步率增长研究（上）——对中国1985-2009年工业”结构红利假说“的检验

摘要：要素流动推动着经济结构的变化，并且影响着技术进步水平的增长。在估计37个行业的技术进步与资本存量的基础上，本文利用偏离-份额法分析了工业结构变化的技术进步率增长效应。研究发现我国各行业之间的技术进步率在不断改善，资本和劳动力的流动较明显倾向于第二、三类产业；资本要素对技术进步率增长的贡献主要来源于内部增长效应；劳动力变化对技术进步的影响较大，但是主要依靠内部增长效应来促进技术进步率的增长，其中劳动力的流动对第三类产业具有显著的“结构红利”。

关键词：工业结构变化，技术进步率，结构红利假说

一 引言

由于各行业的技术进步率水平和增长存在差异，当投入要素从低技术进步率或技术进步率增长慢的行业向高技术进步率或技术进步率增长快的行业流动时，将会促进相应行业的生产率和技术进步率的增长，这种要素流动而形成的工业结构变化对生产率增长或技术进步率增长的贡献就是所谓的“结构红利假说”。

20世纪50年代以来，国内外不少学者围绕“结构红利假说”进行了大量的实证研究。但是，绝大多数研究都集中于国家层面、省际层面、农业与非农业或三次产业的结构变化对生产率增长的影响，而对工业化过程中深层次的结构变化，即工业行业结构变化对生产率增长影响的研究却极为鲜见，同时所有的研究皆集中于劳动生产率的增长效应，对于在工业化过程中起到至关重要的技术进步率的增长效应却尚无研究。其次从技术进步率的估算方法看，目前测算技术进步的方法主要有指标法（构建评价指标体系）、生产函数法（索洛余值法）、数据包络（DEA）Malmquist指数分解等。指标法能够从不同的角度反映出被评测对象的技术进步状况，但是指标选取较为复杂以及无法综合反映技术进步水平；而索洛余值法存在原理性的错误（周方，1994、1999），数据包络法是评价部门的生产过程在技术水平、生产规模等方面均达到理想条件为假设而确定的，能够较好地反映生产函数的真正意义（张延欣等，1997）。因此，用数据包络方法对我国工业行业的技术进步率进行估算，并针对我国工业行业结构变化与技术进步率增长的关系进行实证研究具有现实意义。

二 技术进步率测算

（一）Malmquist指数分解

Malmquist生产率指数通过计算每个数据点相对于普通技术距离的比值来衡量全要素生产率的变化。我们将每个行业看作一个生产决策单元，基于投入的角度来进行分析，假设在每一个时期，t＝1，2，…，T，第k＝1，2，…，K个行业使用n＝1，2，…，N种投入x^t_k,n，得到第m＝1，2，…，M种产出y^t_k,m。这样，每一期在固定规模报酬（C），要素强可处置（S）条件下的参考技术被定义为：

（1）式中，z为每一个横截面观察值的权重。因此，计算每一个分行业基于投入的Farrell技术效率的非参数规划模型为：

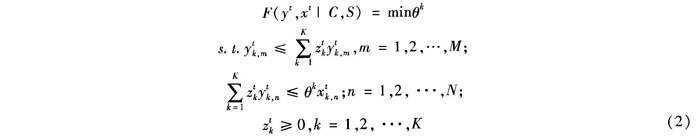
这两个指数分别测度了在时期t和t+1的技术条件下，从时期t到t+1技术效率变化的Malmquist生产率指数。而Malmquist生产率变化指数可以被分解为相对技术效率的变化和技术进步的变化（Fare等，1997）：

（二）数据的处理说明

数据的处理很大程度上决定着最后结论与已有研究文献的不一致，尤其是对资产数据处理的不一致。文中工业总产值、固定资产净值、全部从业人数年平均人数等数据主要来源于《中国统计年鉴》和《中国工业经济统计年鉴》。其中，2004年工业总产值数据来源于《中国经济普查年鉴2004》，由于1993-1998年的固定资产净值数据缺失，作者利用相连年份插值算得，另外1999年以前的全部从业人数年平均人数作者以职工年末人数代替。

1.工业总产值

以工业总产值作为产出，并以各行业工业品出厂价格指数将当年价的工业总产值折算成1985年为基期的不变价。

2.资本存量

对于资本投入，需要考虑资本存量，我们参照李小平、朱钟棣（2005）做法，利用建筑安装价格指数和工业品出厂价格指数计算出固定资产价格指数，然后对固定资产进行折算。计算固定资产价格指数公式为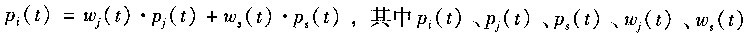：分别表示t年行业i固定资产投资价格指数、建筑安装价格指数、设备价格指数（以各行业：正业品出厂价格指数表示）、建筑安装工程费用占固定资产总值比例和设备费用（包括设备工器具购置和其他费用）占固定资产总值比例。然后对各行业的固定资产净值进行以下折算：

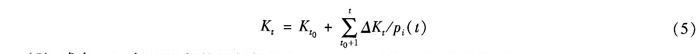
（5）式中，K_to为1985年的固定资产净值，△K_t为t年固定资产净值增量，以相连两年的固定资产净值之差表示。

3.劳动力

针对劳动投入来说，考虑劳动资本存量是较为理想的，但是其数据不可得，因此，我们以全部从业人员年平均人数表示。

（三）中国工业行业技术进步率

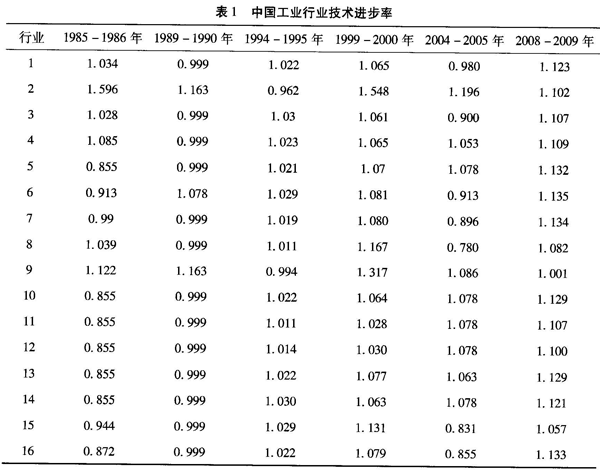
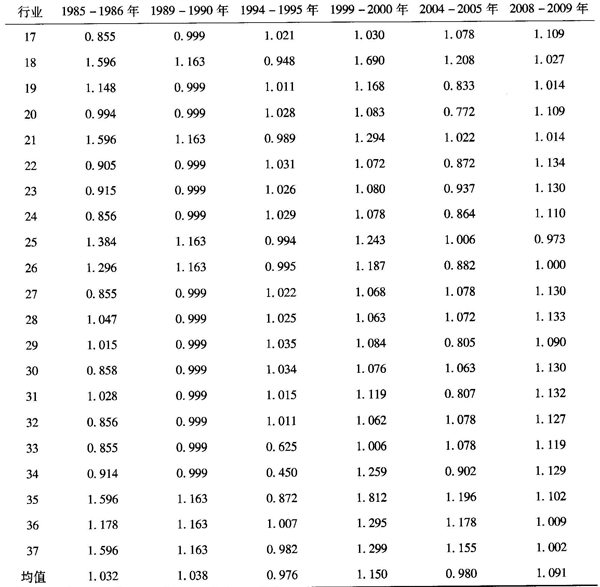
通过运用DEA的Malmquist指数分解得出中国工业37个行业的技术进步率（见表1），从表中可以看出，不同行业相同时间的技术进步率存在较大差异。如1997-1998年的废弃资源和废旧材料回收加工业（5.172）与电力、热力的生产和供应业（0.959）之间的技术进步率差异巨大（差值为4.213）；同时，在不同时间相同行业也存在较大差异，1985-1992、1993-1994和1996-1997年间的各行业的技术进步率多数小于1，这说明这些年工业行业的技术进步率处于退化阶段，而1992-1993、1994-1996和1997-2009年的技术进步率绝大多数大于1，这说明近年来随着工业结构的调整和发展各行业的技术进步率在逐步改善。

三 工业结构变化与技术进步率差异

工业结构变化是技术进步率增长的一个重要原因，也是技术进步率增长的结果，要考察工业结构变化对技术进步率增长的影响，就应该先了解工业结构变化和技术进步率差异的状况。表2报告了1985-2009年中国分行业的工业总产值、全部从业人员年平均人数、资本存量和技术进步率的增长情况。表中显示该时期工业不同行业不同时间的增长速度差异较为明显。从工业总产值看，其平均增长率为18.058%，增长较显著，高于这个平均值的有21个行业，其中增长速度最高的为黑色金属矿采选业（25.419%），增长速度最低的为农副食品加工业（11.467%），二者相差13.952%。从全部从业人数年平均人数看，平均增长率为1.492%，高于平均值的行业有18个，其中行业间的差异较大，增长率最高的通信设备、计算机及其他电子设备制造业（6.461%）与最低的废弃资源和废旧材料回收加工业（-3.953%）之间相差10.396%。从资本存量看，其平均增长率为15.943%，其中有22个行业高于这个平均值，增长率最高的行业通信设备、计算机及其他电子设备制造业（19.597%）与最低的行业机械工业（11.24%）相差8.356%。从技术进步看，平均增长率为0.24%，高于此值的行业有25个，增长最快的非金属矿采选业（1.176%）与最低的化学纤维制造业（-1.872%）相差为3.048%，差距较为显著。从以上的分析可以较为明显地看出，产出和技术进步的增长主要来自于资本存量的贡献。

四 工业结构变化的技术进步率增长效应

偏离一份额法（Shift-Share Analysis）被大多数学者用于考察基于要素流动导致结构变化对生产率的影响，该方法最早是由Vabricant（1942）提出，并经Massell（1961）等人进行了扩展。这方法将生产率的增长分解为结构变化和产业部门内部增长两部分贡献，而结构变化的贡献又可以进一步分解为要素的静态变化效应和动态变化效应。以下我们参考吕铁（2002）、干春晖和郑若谷（2009）的做法，采用偏离-份额法（Shift-ShareAnalysis）来测算中国工业结构变化的技术进步率增长效应。

如果假定TP为工业结构的技术进步率，下标i表示工业行业，下标0表示初始水平，L_i为行业i占工业劳动投入（全部从业人员年平均人数）的比重，K_i为行业i占工业资本存量投入的比重，△TP、△L与△K分别表示技术进步率、劳动投入与资本存量比重的增量，那么则有：

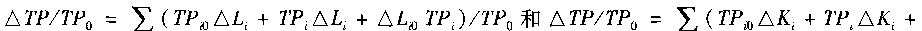
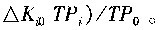
式中右边第一项为静态转移效应，反映劳动（资本）投入向具有较高初始技术进步率水平的行业转移时引致技术进步率的增长效应，即由工业结构的变动所引起的技术进步率上升。如果某期具有较高的技术进步率行业吸收了更多的投入要素，提高了自身的要素份额，则这项符号为正，称为“结构红利假说”。第二项为动态转移效应，是反映劳动（资本）要素向更高增长率的行业流动所带来的增长效应，是工业结构变化与技术进步率变化的综合作用，如果行业部门的要素生产率和要素份额同时增加，则该项为正。反之，如果要素生产率增长较快行业的要素份额较少，或者要素生产率增长较慢行业的要素份额增加，则称为“结构负利假说”。第三项为生产率增长效应，这里为技术进步率增长效应，表示在工业结构不发生变化时各行业要素技术进步率增长的加权和，也是衡量基于每个行业内部的技术进步和技术效率变化等引致各行业内部要素的增长对总体技术进步率变化的贡献。