基于时序图模型结构估计的股票联动研究

     内容提要：我国股市个股价格同时上涨或同时下跌的联动现象极为普遍，传统上使用向量自回归、协整、有向非循环图等方法主要用于少量股票或市场之间的联动性研究，不适于直接对大规模个股之间的联动关系进行研究。文章关注大规模时序图模型结构建立及估计方法，通过将ADL方法引入SPACE算法，提出了可以估计高维低样时序图模型的ADL-SPACE算法；设计模拟实验考察了算法中惩罚参数λ值的设置对于节点自回归相关性捕获的有效性；在实证研究中，文章使用了ADL-SPACE算法对个股联动研究了三方面的内容：1.基于个股联动的代表性行业之间的联动性；2.设计了我国A股市场中行业联动强度，对行业内外联动性进行综合评价和分析；3.采用一阶滞后个股基于时序图模型结果构造了投资组合，模拟显示收益预期表现良好。以上研究均表明时序SPACE图模型方法在大规模股票的联动探测中有较好的应用前景。
关键词：图模型/时序SPACE算法/股票联动
    作者简介：王星，朱建旭，中国人民大学应用统计科学研究中心，中国人民大学统计学院（北京100872）。
        0引言
    股票联动是股票关联关系中的一种常见的关系，表示板块内或板块之间个股价格同时上涨或者同时下跌的运动。在复杂多变的证券市场中，通过对股票市场中股票的关联分析，进而根据板块价格演变规律指导投资实践具有指导意义[1]。研究股票联动不仅能够发现具有经济内涵的股票群落，而且有助于对由联动股票所构成的有机整体规律的认识与把握，从而可以更深刻地把握资产组合的价值和内涵[2]。
    在股票联动的研究方法中，直接研究股票之间联动的方法并不多见。Huang BN[3]、王凯涛[4]、何芳等[5]主要采用了协整理论、格兰杰因果检验等方法对资本市场的联动问题进行了大量研究，这些研究方法是将一个市场比如沪市、深市或整个市场作为研究对象，得到的是股票宏观层面的联动规律。杜伟锦，何桃富[6]研究了微观情形下股票联动问题，采用的是先对股票聚类再研究类别之间的联动，这是一种间接研究联动的方法。近些年来，向量自回归模型在分析联动方面得到广泛应用，代表性的研究如陈燕明等[7]。此外，吴英杰[8]、蔡风景[9]等人使用有向非循环图DAG结合偏相关检验产生因果动态图对我国股票市场联动进行研究。这些方法只能局限于对少量股票或股票类（板块）之间的联动性进行研究，因为DAG所依赖的方向标注在规模较大的网络结构中的理论不够成熟，这也是传统设计计算中的难点部分，常常伴随大量的计算代价，得到的结果稳定性不佳[10]。
    本文将尝试能够对大量股票进行联动研究的微观分析方法，在这方面，汪廷华[11]使用了关联规则方法研究了我国A股市场的股票联动问题。以个股收益率相关性为例，关联规则中的相关系数，不能表示两支个股之间的因果关系，因为找出的两支个股的收益率可能本质上没有任何联系，它们之间数量上的强相关是因为包含了第三支股票的收益率而产生的，个股之间的因果联动常常是投资者最期望的信息。所以，基于相关测量所产生的联动关系可能是伪关系。综上所述，研究高维股票序列联动的测量模型和计算方法具有积极意义。
    股票和股票之间的联动可以用一个图G=（V，E）表示，其中V代表股票集，E代表两支股票之间的联动关系，联动关系是两两关系，所以应使用偏相关系数通过图模型研究股票之间的关系。Meinshausen和Buhlmann[12]、Yuan和Lin[13]、J Peng，Ji Zhu[14]等人提出使用图模型算法用于多变量偏相关关系的研究，但这些研究没有假设节点是时序的情况，所以不能直接应用于股票的联动分析中。本文将考虑适用于股票联动分析需要的时序图模型，评价时序图模型在揭示股票联动性上的作用。以下将分三部分阐述ADL-SPACE算法的基本思路：第一部分简要回顾偏相关图模型SPACE算法理论，在此基础上重点阐述时序图模算法ADL-SPACE的设计原理，给出高维时序算法的具体计算过程；第二部分设计模拟实验，评估新提出算法在时序数据联动性上的作用；第三部分给出ADL-SPACE算法研究我国A股市场的联动研究和相关结果。
    1SPACE算法和ADL-SPACE算法
    1.1SPACE算法
    SPACE算法是J Peng，Ji Zhu等[14]提出的图模型偏相关结构估计算法，该算法构造了一个解偏相关系数的一阶罚模型，该模型的主要作用是解决DAG方法在处理大规模图主图结构提取问题，称为联合稀疏回归模型（Joint Sparse Regression mod-el），如公式（1）所示：
     
    算法1适用于强偏相关性数量不多的高维稀疏图模型的结构性参数估计，不仅可以高效地估计偏相关系数，而且可以将数值接近零的偏相关系数在计算过程中置为零，从而达到提取主图结构的目的。由于引入Lasso的设计，它还能提取图模型里面的枢纽节点（Hub）项，即和很多节点都存在强偏相关关系的节点，这些特征都为直接研究股票联动关系提供了重要的结构信息。
    1.2SPACE算法中多元估计问题的解决—Shoot-ing算法
    因变量一元的情况下，Lasso回归的参数估计常使用LARS算法迭代产生，但在多元情况下，对Lasso回归的参数估计会比较困难。Fu[15]提出了估计多元Lasso参数的Shooting算法，其基本思想是：用普通多元回归的参数估计值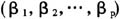作为初值，通过迭代更新每个估计值：从第一个参数开始，固定其余的p-1个变量，用一元回归的参数估计更新这个变量；第二步为固定其余的p-1个变量，用一元回归的参数估计更新第二个变量…如此迭代直至收敛，如图1所示。
     
    算法1中的Lasso回归涉及到的变量维数为p（p-1）/2维，如果p较大，直接使用Shooting算法解算法1中的Lasso回归效率会比较低。J Peng，J Zhu等[14]在Shooting算法的基础上发展了更有效的Active-Shooting算法。其计算步骤为：
    第一步，先用Shooting算法找到参数的一个非零Active集；
    第二步，用Shooting算法更新目前Active集的系数直到收敛；
    第三步，在全变量集上用Shooting算法再做一遍，如果在这个过程中参数值没有改变，那么把这个参数作为最终估计的估计值。否则回到第二步。
     
    1.3ADL-SPACE算法
    现存时间序列关系的方法，如VAR、协整、ADL等，都有一个共同的特点：当分析两个时间序列之间的关系时，都会将其中一个序列作为内生变量，将该序列自身的滞后项、另一个时序和它的滞后项作为外生变量建立回归；如果第一个序列和第二个序列以及第二个序列的滞后项之间的回归系数不显著，那么可以认为内生序列与外生序列是无关的。于是，在处理高维低样时序图模型的一个自然的想法是：把每个节点的滞后项纳入图模型的设计中，如：把每个节点的q阶滞后项作为节点加入图中，用已有的适合高维低样的稀疏图模型算法来估计图模型，具体设计如下：
     
    考虑构造含有每个节点的q阶滞后项的ADL-SPACE回归模型（Joint Sparse Regression model），如公式（3）：
     
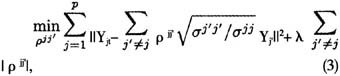
    用迭代算法求出变量之间的偏相关系数，迭代算法为算法2，如下所示。
    算法2ADL-SPACE回归模型的迭代算法
     
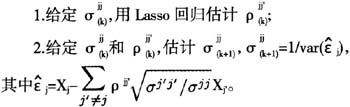
    对于算法2中的Lasso回归，使用Active-Shooting算法估计。
    ADL-SPACE算法继承了SPACE算法的三个优点。（1）可以以高效估计高维低样的时序图模型；（2）由于所有节点间的偏相关系数是一起被估计的，所以ADL-SPACE算法避免了邻域选择方法的不稳定性；（3）能够发现枢纽（Hub）节点。
    2实验模拟和参数范围确定
    ADL-SPACE算法设计中的关键部分是惩罚项λ的确定。第三部分希望通过设计模拟实验考察ADL-SPACE算法对真实模型的提炼能力，比较ADL-SPACE算法调节λ值对结果的影响。
    首先构造图模型为：100个节点，每个节点48个样本，其中前50个节点是彼此独立的且服从均值为0、协方差阵为对角阵的多元正态分布；后50个节点，每个节点满足AR（1）模型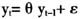：，ε～N（0，0.3）。
    该模型的真实情况是：无法判断后50个数据点是满足AR（1）模型的节点间的真实偏相关系数；已知的真实情况是：前50个彼此独立的服从正态分布的节点和其一阶滞后节点间的偏相关系数是0；后50个节点和其一阶滞后节点是偏相关的。
    由于只知道图模型的部分真实情况，所以需要定义新的模型误差率来验证ADL-SPACE算法的效果。图模型的部分真实情况是：所有100个节点和其滞后项节点的偏相关关系和前50个节点间的偏相关关系。这里，定义模型误差率1和模型误差率2反映ADL-SPACE算法的效果：
    模型误差率1=前50个节点和其滞后项有边的个数/50；
    模型误差率2=1-（后50个节点和其滞后项有边的个数/50）。
    如果模型误差率1为0，那么说明ADL-SPACE算法把前50个节点和滞后项的偏相关关系都判断对了，即前50个节点和滞后项之间都没有边。模型误差率1越小，说明ADL-SPACE算法在正确判断两个节点的条件独立性越好。如果模型误差率2为0，那么说明ADL-SPACE算法把后50个节点和滞后项的偏相关关系都判断对了，即后50个节点和滞后项之间都有边。模型误差率2越小，说明ADL-SPACE算法在正确判断两个节点有边的效果越好。表1和表2是当θ和λ取不同值时，模拟数据拟合ADL-SPACE算法的模型误差率1和模型误差率2：
     
     
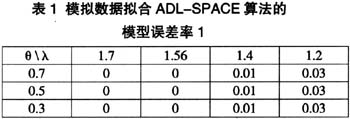
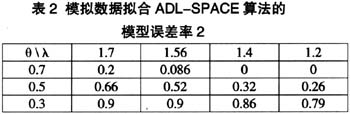
    根据表1和表2中可以看出，当θ≤0.3时，因为其后50个节点和自身的时序相关较小，所以，无论如何调整λ值，已经比较难以发现实际存在的边。当θ≥0.7时，使用合适λ值（如1.56、1.4）的ADL-SPACE算法基本上可以发现存在的边。当θ在0.5左右，λ在1.56左右时，ADL-SPACE算法有一半的概率能够发现真实存在的边。
    综上所述，当λ取值在1.4到1.56之间时，ADL-SPACE算法能发现偏相关关系较强的边。如果λ取值过小，ADL-SPACE算法会把没有边的误判为有边；如果λ值取大值，会将有边的判为没有边。在问题中，由于要探索节点和节点之间的强偏相关关系，所以可以倾向于把λ值调大一点。
    3ADL-SPACE算法对我国A股市场联动的研究
    该部分使用ADL-SPACE算法研究我国A股市场股票联动问题，主要研究内容有以下三项：
    1.金融保险业和采掘业的各阶联动分析；
    2.A股市场的全体股票与一阶滞后项的联动关系；
    3.使用ADL-SPACE算法构造资产组仓。
    3.1金融保险业和采掘业个股收益和其一阶、二阶滞后收益的联动分析
    选择了两个行业间联动较为活跃的蓝筹行业金融保险和采掘业作为代表，研究不同行业之间的联动特点。数据来自巨灵金融数据库，提取金融保险业和采掘业2006年2月28日到2010年1月31日的月收益数据，去除掉2006年以前上市的企业以及停牌的企业共有35家。使用该数据拟合二阶滞后的ADL-SPACE算法。结果如图3所示。
    图3中E、E1和E2点代表金融保险业个股收益原数据，一、二阶滞后项，F、F1和F2点分别代表采掘业个股收益原数据，一、二阶滞后项。图3表明，金融保险业和采掘业的原数据（Metadata）和其一阶滞后、二阶滞后基本上没有联动关系。我们发现各阶中两个行业之间都存在一些股票之间有强偏相关关系。考虑当期收益和滞后期收益的联动问题：如果某个行业有很多个股当期月收益和其滞后一阶月收益有很强的关系；那么市场就会出现很多无风险套利机会。根据有效市场假说，不可能出现太多的无风险套利机会。所以这个结果是合理的，但这并未表明A股市场所有的个股都没有时序相关，仍然有不少的个股收益和其他个股收益的滞后有联动关系，所以有必要使用ADL-SPACE算法探讨A股市场的联动问题。
     
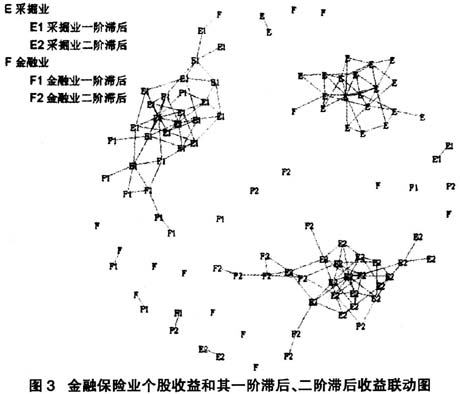
    在图3中，发现和一阶滞后的节点偏相关的原数据的节点很少，和二阶滞后的节点偏相关的更少；所以在第三部分设计中，只使用了拟合一阶滞后的ADL-SPACE算法研究我国A股市场的联动问题。
    3.2A股市场全体个股收益和其一阶滞后的联动分析
    3.2.1A股市场全体个股收益和其一阶滞后的联动图模型估计
    股票市场中的一个流行的观点是：几乎没有完全的有效市场，市场总受各种各样的因素影响，例如股市受政策的影响太大，被一些学者称为“政策市”。所以可以认为某个国家股市部分有效，比如该国市场80%或者95%有效。假设我国A股市场只有5%的关于个股滞后的无风险套利机会，那么探索这种机会仍然是有价值的。所以，有必要使用ADL-SPACE算法研究我国A股市场的联动问题。
    提取A股市场共1280支个股（去除2006以后上市的个股）2006年2月28日到2010年1月31日间的月收益数据，用该数据拟合一阶滞后的ADL-SPACE算法，进行联动分析（这里只要偏相关系数大于0.001就认为两个为节点有边），结果如图4所示。
    从图4中可以看到：只存在少数的个股收益和自己或者其它个股的一阶滞后收益有联动关系。为了ADL-SPACE算法确实是有效的，设计了如下实验：将当期收益和自己或其它一阶滞后收益强偏相关的个股都找出来（设计偏相关关系大于0.03的一共有5对节点为有强偏相关关系个股），对之间有强偏相关关系的两个节点（其中一个是滞后节点）做线性回归。如果每对节点之间的确有很强的线性关系，那么ADL-SPACE算法确实是有效的，即能够把当期收益和自己或其它一阶滞后收益强相关的个股都找出来。表3中的回归结果中显示：ADL-SPACE算法确实找出了当期收益和自己或其它一阶滞后强相关的个股。
     
     
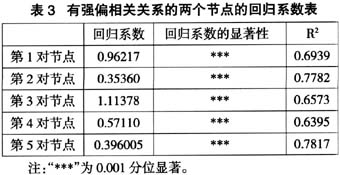
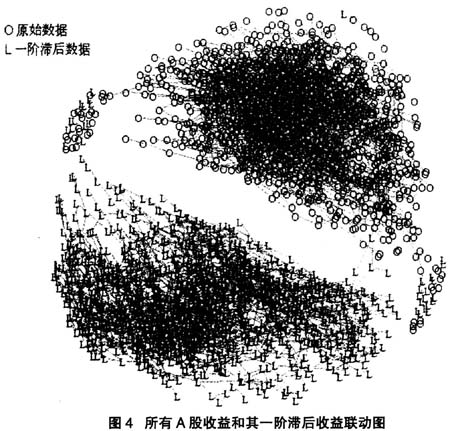
    （图4中O代表A股市场个股收益原数据，L点代表A股市场个股的一阶滞后的收益）
    3.2.2A股市场全体行业的联动强弱分析
    以3.2.1中ADL-SPACE算法估计的模型，进行联动强弱分析。考虑每支个股所属的行业（这里使用的行业是证监会二级行业），结合前面的研究发现，不同的行业内的联动程度确有很大不同；为了量化这些差异，本文定义以下3个指标表达行业内个股的联动强弱：
    （1）内边密集数=每个行业内部节点的连接数之和；
    （2）外边密集数=每个行业内部节点和其他行业的节点连接数之和；
    （3）内边外边比=内边密集数/外边密集数*行业规模系数；其中行业规模系数=1/该行业股票数。
    内边密集率指标表达行业内个股的联动程度，如果某个行业该值为1，那么该行业的每支个股都有边相连，这表示该行业的联动程度最高。某个行业的内边密集率越大表示这个行业的联动程度越高。
    外边密集率指标表达某个行业和其它行业的联动程度。如果某个行业的节点和其他行业的节点的边越多，即外边密集率越大，表示这个行业和其它行业联动程度越高。
    内边外边比表达某个行业个股之间的联动程度和该行业与其它行业个股的联动程度的比较。某个行业的内边外边比越大表示该行业内的联动程度相比行业外的联动程度越大。因为某些行业不仅行业内联动程度很强，行业外联动程度也很强。该指标的价值在于能真正反映某个行业内的联动程度。
    使用2006年2月28日到2010年1月31日间的全体A股月收益数据拟合SPACE算法，并计算每个行业的内边密集率、外边密集率、内边外边比。表4是按照内边外边比指标对行业的排名。
     
    表4的结果显示，综合考虑各行业规模，排名靠前的行业如金融保险业、采掘业、房地产业、农林牧渔等盈利状况更依赖于经济的大环境，例如金融保险业上市公司的业绩（资产基本面价值）和金融市场有相当大的关系；采掘业国有化程度较高，产品差异较小，因而其上市公司的业绩往往在行业内差别不大。所以这些行业的个股收益率在行业内联动性较强。
    传播与文化产业、木材家具、综合类、纺织服装皮毛等这些行业因为其市场化程度较高、竞争非常激烈，所以这些行业的上市公司的业绩更依赖于经营者的素质。因此，对于证券分析师或投资者，如果某支个股属于排名靠前的行业，那么更应该关注该行业的动态，因为该个股的收益更依赖于行业的状况；如果某支个股属于排名靠后的行业，那么更应该关注该个股本身。或者说，投资者应该更加关注排名靠前行业的整体状况和排名靠后行业的个股状况。
    3.3使用ADL-SPACE算法构造资产组合
    本节使用ADL-SPACE算法构造资产组合。在资产组合理论中，一个组合的好坏主要由该组合的收益和市场收益相比。如果所构造的资产组合经实践证明在长期内（一般大于3年）可以取得比市场高的收益，那么所构造的组合就是成功的，这称为跑赢大盘。
    投资于指数型基金或者相应的ETF指数基金可获得约等于大盘的收益。因此，跑赢大盘是所有投资者，特别是机构投资者目标。但是事实上，巴曙松指出80%以上的基金在长期的投资过程中其收益都小于大盘，2008年上半年我国跑赢大盘的基金不到10%[16]。
    所构造组合数据来自2008年1月31日开始，使用2006年2月28日至2007年12月31日期间的23个月收益数据拟合ADL-SPACE算法，找出和滞后项有偏相关关系的个股（如B股收益的一阶滞后和A股收益有正的偏相关关系）。用月上涨买入组合方法进行投资组合设计，具体而言：当B股收益的一阶滞后和A股收益有正的联动关系时，如果A股上月上涨，那么该月买入1股B股；当B股收益的一阶滞后和A股收益有负的联动关系时，如果A股上月下跌，那么该月买入1股B股（简称组合策略）。然后在2008年1月31日计算此次投资的收益。把2008年1月31日的全体个股的月收益数据加入上次拟合算法的数据之中再次拟合ADL-SPACE算法得到结果，找出和滞后收益有偏相关关系的个股，按照组合策略进行投资，并在下个月获得收益，不断循环…。
    具体的资产组合如下：
    第一步，按日期从前到后对A股市场全体个股的月收益进行一行一行的排列，取出前面23个数据作为初始原数据。
    第二步，用原数据拟合ADL-SPACE算法得出结果，原数据是不断变化的，每一个循环有一个新的样本加入。
    第三步，在结果中找出和滞后收益有偏相关关系的个股，使用组合策略进行投资，并在下个月的月底计算收益。
    第四步，把下个月底A股市场全体个股的月收益数据加入原数据拟合模型，即回到第二步…。
    最后得到该组合共25个月的收益率，并与市场收益率相比，如图5所示。
     
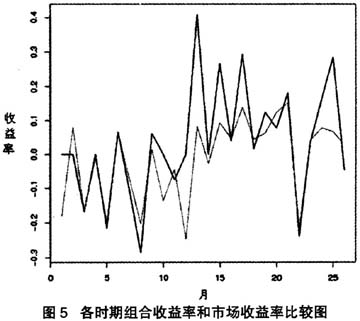
    （黑线代表组合收益，绿线代表市场收益）
    图5显示：长期来看，ADL-SPACE构造的组合收益率明显比市场收益率要高，在经过一个熊市和一波牛市之后（2008年上证指数大幅下降为熊市，2009年到2010之间上证指数大幅上涨为牛市），构造的组合每月平均收益率为0.03431412，而市场平均收益率为-0.01490669。并且，在2008年熊市的时候ADL-SPACE组合下跌幅度和市场相当，但2009年牛市时，ADL-SPACE方法设计的组合收益率远高于市场收益率，于是根据ADL-SPACE所获得的联动关系，可以成功地构造收益良好的组合。
    4结论
    文章旨在提出能够对大量股票直接进行联动研究的分析方法，受向量自回归VAR等通过引入滞后项研究时序相关问题的启发，将ADL模型引入SPACE模型之中，提出了可以处理高维低样时序图模型的ADL-SPACE算法。模拟实验显示ADL-SPACE算法在合适的λ范围中，可能选择出真实的联动关系，于是可以作为研究股票联动分析的工具。文章使用SPACE算法和ADL-SPACE算法尝试研究和探讨了我国A股市场中同一行业的个股联动问题。文章发现股市中各行业的联动程度是不一样的：有的行业间个股同涨同跌的程度会比较高，如金融、保险业；有的行业个股同涨同跌的程度会比较小，如电子行业。本文通过定义“内边外边比”指标合适的反映了不同行业间个股的联动强度。在使用SPACE算法估计出图模型后，本文计算出各行业的“内边外边比”指标，并按“内边外边比”指标进行行业排名。通过排名对各行业的主联动程度有了准确的、数量化的理解。
    文章使用ADL-SPACE算法构造了一个平均收益良好的投资组合，印证了文章所提算法在实践中的有效性，可以发现节点间隐藏的重要联系。这些研究对于设计有价值的投资组合和产生行业联动强度指标值具有一定的指导作用。股票联动的内容很多，比如风险与收益率互联问题也是金融领域里比较关心的问题，文章主要关注股票价格之间的联动设计和计算，如何根据金融市场的背后机制和影响因素展开更深入的联动分析算法设计还需要进一步深入研究。

    参考文献：
        [1]何诚颖.中国股市板块现象分析[J].经济研究，2001，12：82-87.
    [2]李天德.中国股票市场与国际主要股票市场的联动分析[J].统计与决策，2008，18：125-127.
    [3]Huang B N. Causality and Cointegration of Stock Market among the United States, Japan, and the South China Growth Triangle[J]. International Review of Financial Analysis,2000, 9:281-297.
    [4]王凯涛，黄兴旺，陈金贤等.沪深A、B股市场之间的联动效应[J].武汉科技大学学报(社会科学版)，2002.3：20-23.
    [5]何芳.证券间收益的联动效应及实证研究[D]：[硕士学位论文].武汉：2004，武汉大学.
    [6]杜伟锦，何桃富.我国证券市场的板块联动效应及模糊聚类分析[J].商业研究，2005，22：41-45.
    [7]陈燕明.涨跌停板制度下沪深股市向量自回归模型及波动性的协整分析[J].统计教育，2009，11：24-29.
    [8]吴英杰.全球金融危机背景下的股市联动性变化——基于DAG和结构VECM的实证分析[J].南方金融，2010.4：64-70.
    [9]蔡风景等.基于VAR和DAG的中国经济增长实证研究[J].数理统计与管理，2009，28(2)：270-276.
    [10]David Easley and Jon Kleinberg. Networks, Crowds, and Markets: Reasoning about a Highly Connected World [J]. Cam-bridge University Press, 2010.
    [11]汪廷华，程从从.一种元规则指导的股票联动关联规则挖掘算法[J].计算机工程，2006，5：260-262.
    [12]Meinshausen, N and Buhlmann, P. High-dimensional Graphs and Variable Selection with the Lasso [J]. Ann. Statist.2006, 34: 1436-1462.
    [13]Yuan, M and Lin, Y. Model Selection and Estimation in the Gaussian Graphical Model [J]. Biometrika, 2007, 94(1), 19-35.
    [14]Jie Peng, Pei Wang, Nengfeng Zhou and Ji Zhu. Partial Correlation Estimation by Joint Sparse Regression Models [J]. Journal of the American Statistical Association, 2009, 104: 735-746.
    [15]Wenjiang Fu. Penalized Regressions: The Bridge vs the Lasso [J]. JCGS, 1998, 7: 397-416.
    [16]巴曙松，陈华良，王超.2008年中国基金与资产管理行业发展报告 [M].北京：中信出版社，2008，9-12.