变额年金业务的风险度量与分析

    内容提要：变额年金产品具有给付投保人最低保证收益率的特点，使资本市场下滑风险从投保人转移到保险公司，但是风险的大小尚不明确。本文建立资产随机模型并使用破产概率和尾部期望损失两个指标度量保险公司销售最低生存利益保证保险（GMLB）和最低身故利益保证保险（GMDB）承担的风险。结果表明最低保证收益率对GMLB的风险有显著影响，而对GMDB没有，在最低保证收益率既定的条件下保险公司投资于股票的份额对风险有显著影响。
    关键词：变额年金/最低保证收益率/破产概率/尾部期望损失
    作者简介：李冰清，博士，南开大学风险管理与保险学系教授；廖朴，南开大学风险管理与保险学系博士生研究生（天津300071）。 
        一、引言
    变额年金产品近年来在国外市场上取得了巨大成功，它提供给投保人一个最低收益保证以免去资本市场下滑风险，并给予投保人获取更高收益的权力。我国从2011年5月开始在北京、上海、广州、深圳和厦门5个城市试点变额年金保险，但是目前仅金盛人寿保险有限公司和中美联泰大都会人寿保险有限公司推出了相关产品，其他大部分公司均持观望态度。保险公司没有全面清楚了解变额年金产品的风险结构以及风险大小是变额年金供给不足的主要原因之一。因此本文度量和分析变额年金的风险。
    很多学者已经研究了变额年金的相关问题：在定价方面，Hardy（2003）通过建立Black-Scholes框架在风险中性概率测度下研究了变额年金的定价问题，暗含的假设是保险公司销售了大量产品进而消除了死亡风险；Milevsky&Sailbury（2006）详细研究最低退保利益保证型变额年金（GMWB）的定价和风险；Bauer et al.（2008）建立了所有类型变额年金均适用的定价框架；Bélanger et al.（2009）研究了允许部分退保的最低死亡利益保证型变额年金（GMDB）的定价方法；Bacinello et al.（2011）从投保人角度出发，结合不同行为特点制定变额年金产品的价格；Cheuk-Yin Ng和Li（2011）使用多维Esscher变换对建立在多个资产上的变额年金产品定价。在风险管理和套期保值方面，由于变额年金产品市场是不完全的，因此德尔塔套期保值方法变得不适用，学者们使用分位数套期保值方法（Quantile Hedging）研究GMDB的套期保值方法，如Wang（2009）、Klusiket al.（2011）；另外最优控制的相关理论也被用于变额年金产品的对冲和风险管理，如Nteukam T et al（2011）；Graf et al.（2011）建立了一种投资连结保险产品的风险分析框架，简化了保险公司投资连结类产品的风险分析。
    本文采用Graf et al.（2011）的基本框架研究变额年金中的最低生存利益保证保险（GMLB）和最低身故利益保证保险（GMDB）两类产品的风险，采用破产概率和尾部期望损失两种指标度量其大小，并借助数值模拟定量分析两类指标。
    二、市场环境
    若只考虑保险公司的变额年金业务，期初变额年金业务的资产A（0）应该与期初的负债L（0）相等。其中，资产是指保险公司因变额年金而持有的资产的市场价值（假设自有资产为0）；负债是指保险公司因变额年金而承担的负债的市场价值。但是在0时刻以后，保险公司的资产和负债不是同步变化的，下面我们分别对变额年金业务的资产和负债建立模型，模拟其价值过程。
    （一）资产模型
    根据中国保监会的规定，保险公司可以投资于风险资产和无风险资产，其中风险资产包括债券、股票、不动产等，无风险资产主要是指现金、国债、央行票据等，本文将这些资产简要概括为银行存款、长期债券和股票三类。
     
     
     
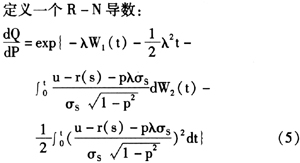
    不难看出，保险公司的总资产过程是一个自融资过程，对任意的t∈[i，i+1）
     
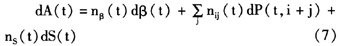
    通过计算，可以得到A（T）服从对数正态分布，其均值和方差分别为：
     
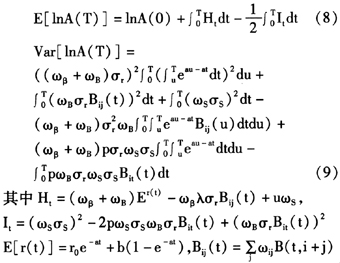
    （二）负债模型
    不同变额年金产品具有不同的特点，因此其负债的形式也有所不同。本文关注最一般的两种产品，即最低生存利益保证保险（Guaranteed Minimum Living Benefit，GMLB）和最低死亡利益保证保险（Guaranteed Minimum Death Benefit，GMDB）。
    1.GMLB
    假设保险公司销售了N份GMLB，投保人的年龄均为x岁，每份GMLB的价格为P，期限为T。因此A（0）=NP，在期满时刻，保险公司的期望负债为：
     
     
    三、变额年金业务的风险度量
    本文选取破产概率和尾部期望损失两种风险度量方法度量变额年金业务风险。破产概率和尾部期望损失是两类常用的风险度量方法，在保险公司的产品定价和产品管理中被经常应用。在产品定价时，保险公司确定风险附加以保证业务在某个置信水平下不破产，或者直接在未来现金流出的精算现值上附加尾部条件期望的一定比例确定保险产品的价格；而在产品的风险管理上，破产概率和尾部期望损失直接反映保险公司的风险大小和管理者的经营水平。破产概率是指保险公司总资产不足以支付L（T）发生的概率，即：
    p|A（T）＜L（T）|
    尾部期望损失是指超出资产的负债的尾部期望，即：
     
    四、风险分析
    （一）风险内容及参数假设
    我国变额年金业务正在经历从无到有的过程，经营变额年金业务的保险公司关注的风险包括许多方面，结合本文模型，我们分析以下两个方面内容：第一是最低保证收益率对变额年金的影响。变额年金业务与投资连结险业务或万能险业务最主要的区别在于赋予投保者最低收益保证，那么保险公司关注最低保证收益率的高低如何影响风险。第二是资产配置对变额年金的影响。由于赋予投保人最低收益的保证，那么保险公司面临的负债结构发生了变化，使得保险公司将采用与其他保险产品不同的投资结构和方式。因此保险公司关注不同资产配置方式如何影响风险。
     
     
     
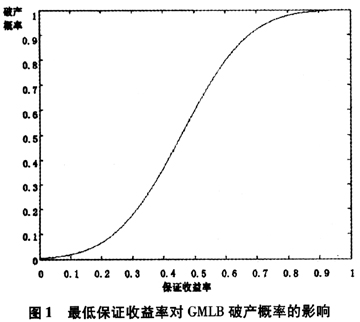
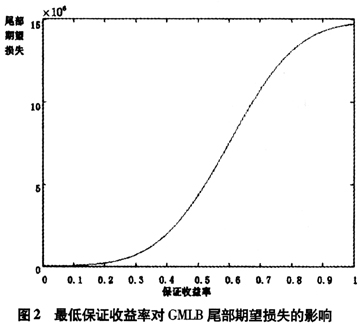
    从图1和图2可以看出，随着GMLB赋予的最低保证收益率增加，保险公司所面临的风险越大。当保证收益率为0时（即g=0），保险公司的破产概率为0.0038，尾部期望损失为6565.70；而当保证收益率为5%（即g=0.05），保险公司的破产概率为0.0087，尾部期望损失为16749。
    GMLB的风险也将因为保险公司在三类不同证券上分配的比例而改变，如表1所示（假设保证收益率为5%）。
     
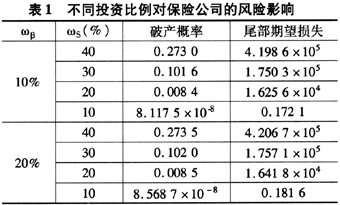
    从表1可以看出，投资于股票的资金份额越大，保险公司面临的风险越大：当保险公司将所有资产的40%投资于股票市场时，它发生支付短缺的概率约为0.27；当保险公司将所有资产的20%投资于股票市场时，它放生支付短缺的概率下降为0.008。其他资产份额的变化对保险公司的风险影响远远不如股票资产，当股票份额不变，债券和银行存款之间份额的10%转换几乎对保险公司的风险不造成影响。从尾部期望损失的数值可以看出，保险公司持有股票的份额也对保险公司的尾部期望损失产生较大影响，当股票份额由20%减少为10%时，保险公司几乎预期不发生损失。
    （三）GMDB
    按照与GMLB相同的模式，我们可以对GMDB进行风险分析。根据图1和图2的相关假设，可以得到GMDB的风险测度随最低保证收益率的变化图。
    从图3和图4可以看出，随着GMDB赋予的最低保证收益率增加，保险公司所面临的风险越大，但是这种增大的过程很缓慢。当保证收益率从0.1增加到0.7时，保险公司的破产概率从2.3978e-010增加到2.2496e-004，尾部期望损失从2.0570e-005增加到192.7391。
     
     
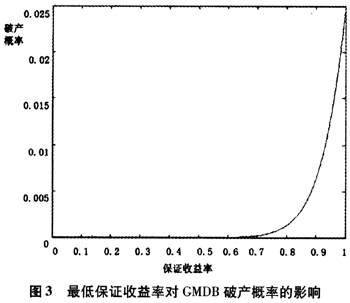
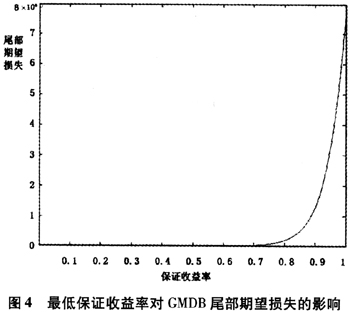
    虽然GMDB的风险对比没有GMLB那么明显，我们仍然可以分析不同股票投资比例对保险公司的影响。如表2所示（假设投资收益率为80%②）。
     
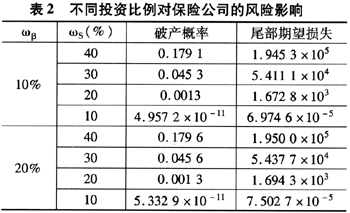
    在这种情况下，我们可以得到与GMLB相似的结论，这里不再赘述。
    五、结论
    本文在以下假设条件下建立了变额年金的风险度量与分析框架：第一，保险业务的期初资产全部来源于保费收入；第二，保险公司在期初决定投资于股票、债券和银行账户的资产比例，并保持不变；第三，在GMDB中死亡保险金按无风险利率积累到期末给付。根据本文的分析，可以得到以下结论：
    变额年金产品需要在风险以及市场欢迎程度之间进行抉择，保证收益率越高，保险公司推行的变额年金产品越能得到市场欢迎，但是此时保险公司面临的风险也越大。保险公司可以根据公司风险承受能力选择适当的最低收益率保证，如在本文中，将GMLB的最低保证收益率设定为5%，可以保证公司以99%的概率不破产。
    保险公司可以选择适当的股票投资份额，以综合满足公司风险管理要求和市场需求。保险公司投资于股票市场的资产份额越大，面临的风险越大，投保人获得高收益的可能性越大。保险公司可以根据公司的风险承受能力选择适当的最高股票投资份额，如在本文中，如果最低保证收益率为5%，公司最高股票投资份额约为15%。
    注释：
    ①这可能与真实的情况不完全相同，但是考虑到保险公司可以随时切换，本文假设如此。
    ②这显然很不符合实际，但是采用此数值能够更明显反应保险公司风险随资产配置的变化。
        参考文献：
    [1]黄德龙，杨晓光.中国证券市场股指收益分布的实证分析[J].管理科学学报,2008，(11).
    [2]谢赤，吴雄伟.基于Vasicek和CIR模型中的中国货币市场利率行为实证分析[J].中国管理科学，2002，(3).
    [3]郭磊.中国年金市场养老保险公司竞争互动研究[J].保险研究，2011，(10).
    [4]王旭，邱华龙.变额年金在我国的应用及风险管理探讨[J].保险研究，2011，(11).
    [5]韩猛，王晓军.我国年金产品效用比较[J].保险研究，2010，(4).
    [6]Bacinello, A. R., Millossovich, P., Olivieri, A., Pitacco, E.. 2011. Variable annuities: A unifying valuation approach[J]. Insurance: Mathematics and Economics, 2011, 49: 285-297.
    [7]Barbarin, Devolder. Risk measure and fair valuation of an investment guarantee in life insurance[J]. Insurance: Mathematics and Economics, 2005, 37: 297-323.
    [8]BAUER, Daniel, KLING, Alexander, RUSS, Jochen. A universal pricing framework for guaranteed minimum benefits in variable[J]. ASTIN Bulletin, 2008, 38:621-651.
    [9]Bélanger, A. C., Forsyth, P. A. and Labahn, G, Valuing the guaranteed minimum death benefit clause with partial withdrawals[J]. Applied Mathematical Finance, 2009, 16: 451-496.
    [10]Cheuk-Yin Nga, Johnny Siu-Hang Li. Valuing variable annuity guarantees with the multivariate Esscher transform[J]. Insurance: Mathematics and Economics, 2011,49: 395-400.
    [11]Hardy, M. R.. Investment Guarantees: Modeling and Risk Management for Equity-linked Life Insurance[M]. John Wiley & Sons, Hoboken, New Jersey. 2003.
    [12]Milevsky, M. A.. Salisbury, T. S.. Financial valuation of guaranteed minimum withdrawal benefits[J]. Insurance: Mathematics and Economics, 2006, 38:21-38.
    [13]Oberlain Nteukam T., Frédéric Planchet, Pierre-E. Thérond. Optimal strategies for hedging portfolios of unit-linked life insurance contracts with minimum death guarantee[J]. Insurance: Mathematics and Economics, 2011, 48:161-175.
    [14]Przemyslaw Klusik, Zbigniew Palmowski. Quantile hedging for equity-linked contracts[J]. Insurance: Mathematics and Economics, 2011,48:280-286.
    [15]Stefan Graf, Alexander Kling, Jochen Ruβ. Risk analysis and valuation of life insurance contracts: Combining actuarial and financial approaches[J]. Insurance: Mathematics and Economics, 2011, 49:115-125.
    [16]Yumin Wang. Quantile hedging for guaranteed minimum death benefits[J]. Insurance: Mathematics and Economics, 2009, 45:449-458. Risk Measurement and Analysis of Variable Annuity.^