会员登录
会员注册内容提要：本文研究面板数据空间误差分量模型（Spatial Error Components Model，SEC）的估计方法。为克服极大似然法在SEC模型估计中运算的困难，本文提出基于广义矩估计的可行广义最小二乘法（GMM-GLS），证明了估计量的一致性及有限样本下的有效性；并应用此模型，研究2000年～2007年中国30个省（西藏除外）的物质资本存量、人力资本存量及能源消耗对实际GDP的影响，结果表明，采用SEC模型所得估计结果更为符合经济现实。
关键词：空间误差分量模型/面板数据/广义矩估计作者简介：陈青青，华南理工大学经济与贸易学院（广东广州510006）；龙志和，林光平，波特兰州立大学经济系（美国波特兰97207）。
0引言
近年来，空间经济计量模型被学者们广泛应用于区域经济、社会网络等实证领域。目前，空间计量模型侧重于空间相关性分析，主要包括空间滞后（Spatial Lag，SLAG）模型和空间误差（Spatial Error，SE）模型，分别处理因变量和误差项间的空间相关性。其中，误差项的空间结构较为复杂，是本文重点研究对象。目前，空间误差自相关（Spatial Error Autoregression，SEAR）模型和空间误差移动平均（Spatial Error Moving Average，SEMA）模型是最常见的两种空间误差模型，模型形式分别如下（Anselin，1988[1]）：
SEAR：y=Xβ+ε，ε=ρWε+u，
SEMA：y=Xβ+ε，ε=λWu+u，
式中，y和X分别表示因变量和自变量，ε，u等为误差项，设定u～i.i.d.N（0，
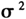）。W为空间权重矩阵，一般进行行标准化，ρ，λ为相应的空间权重系数，为防止误差项方差的奇异性，通常设定｜ρ｜＜l，｜λ｜＜1。文献上，Cliff & Ord（1981）[2]，Anselin（1988，2001）[1，3]、Lee（2004）[4]、Kelejian & Prucha（1998，1999）[5-6]、Kappor、Kelejian & Prucha（KKP，2007）[7]等学者提出了采用极大似然法（ML）、可行广义最小二乘法（GLS）、广义矩估计（GMM）等方法估计上述模型。
不过，尽管在实证研究中得到广泛应用，但Kelejian & Robinson（1993，1995）[8-9]指出，SEAR和SEMA模型仍存在不足之处。第一，空间权重矩阵W的非对称性，以及对ρ，λ的参数限制，将使得模型的参数估计异常复杂，尤其对误差项方差的估算。第二，在实际应用中存在不足，SEAR和SEMA模型中，将空间权重矩阵W设定为非对称矩阵，未能分析经济运行中，研究对象间空间效应相互对等的情形；此外，这两类模型仅仅研究误差项的空间溢出效应，如
，无法同时考虑非空间溢出的经济冲击。为此，Kelejian & Robinson[8，9]提出了截面数据的空间误差分量模型（Spatial Error Components Model，SEC模型），作为传统空间误差模型的替代模型：y=Xβ+ε，ε=Wψ+ξ，
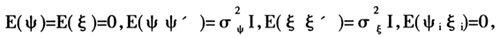
式中，y，X，ε分别代表因变量、自变量和误差项，β为斜率系数，SEC模型将误差项分解为相互独立的两项，分别代表空间溢出项（Wψ）和区域特质项（ξ）。
与SEAR模型和SEMA模型相比，SEC模型没有｜ρ｜＜1等参数限制。同时，模型中空间权重矩阵W可为对称矩阵，不需行标准化，简化了参数估计的运算。在实际经济分析中，W的对称性体现为研究对象间空间溢出效应的对等性，与经济运行现状更为吻合。此外，实际经济管理过程中，如文化差异、产业政策等因素并不存在明显的地区间空间溢出效应，但对经济运行产生冲击。SEC模型的误差项中包括独立的空间溢出项（Wψ）和区域特质干扰项（ξ），更合理地解释现实经济运行状况。
已有文献中，对SEC模型的估计方法研究甚少。理论研究上，仅Kelejian & Robinsont[8-9]采用最小二乘（LS）方法估计方差系数，对整体模型采用可行GLS估计；实证研究上，仅Kelejian & Robinson（1993[8]，1999[10]采用SEC模型研究了美国760个县级区域的警力支出与区域人口和财政支出的关系，以及美国48个州级区域私人总产出与基础设施建设投入的关系，实证结果均表明SEC模型较一般空间计量模型更为合理。
此外，现有的SEC模型估计都是基于截面数据，对面板数据的SEC模型估计研究几乎处于空白。本文讨论面板数据的SEC模型估计方法，全文分五部分，第一部分介绍面板数据SEC模型；第二部分提出SEC模型的GMM估计法；第三部分为Monte Carlo模拟实验；第四部分为实例分析；最后为结论。
1面板数据空间误差分量（SEC）模型
本文将截面SEC模型（Kelejian& Robinson[8-9]扩展至面板数据SEC模型。Baltagi（2001）[11]、Matyas（2008）[12]等认为考虑固定效应将得到不一致的估计量，导致误差项方差矩阵为奇异矩阵，因此，本文引入随机效应，面板数据SEC模型如下：
模型（1）有如下假设：
Greene（2007）[13]认为，ML估计量具有一致性及渐进有效性。因此，本文首先考虑SEC模型的极大似然法估计，将模型（1）排列得到：
在正态分布假设下，似然函数为：
2基于GMM的可行GLS估计
Kappor、Kelejian & Prucha[7]提出面板数据SEAR模型的GMM估计，本文在其基础上提出面板数据SEC模型的GMM估计。
其中，
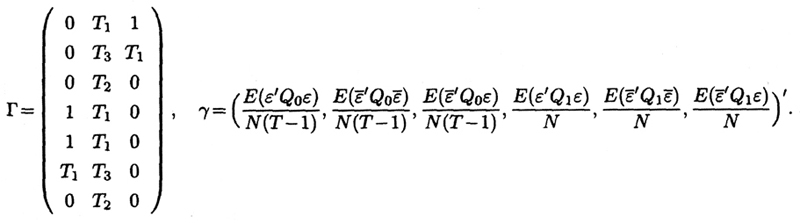
则相应的有：
矩条件的推导及定理一的证明见附录一。此外，Hansen（1982）[15]、Greene（2007）[16]等GMM估计文献中，为得到更为有效的GMM估计量，建议采用矩条件的方差矩阵来构造最优权重矩阵。参考上述文献，本文构造最优权重矩阵如下：
Ξ的推导及定理二的证明见附录二。面板数据SEC模型的可行广义最小二乘法（GLS）估计量为
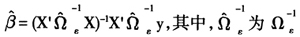的一致估计量，采用等权重GMM和最优权重GMM估计，分别记为等权重GMM-GLS和最优权重GMM-GLS。3 Monte Carlo模拟实验
本节研究面板数据SEC模型GMM估计量的有限样本性质，等权重GMM-GLS和最优权重GMM-GLS估计量分别记为EGMM-GLS和OGMM-GLS，为了进行比较，Monte Carlo模拟实验还考虑了普通最小二乘法（OLS）和广义最小二乘法（Generalized Least square，GLS）估计量（误差项方差采用真实值）。本研究借鉴Das、Kelejian & Prucha[16]和KKP[7]等模拟实验研究方法，考察各种估计量的均方根误（Root Mean Squared Error，RMSE）表现，RMSE定义为：
此外，本研究Monte Carlo模拟实验采用Rook形式的权重矩阵（相邻区域取值1，否则取0），令
=1且保持不变，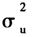
=｛0，1｝，分别表示不存在随机效应和存在随机效应的情形，
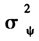=｛0.2，0.75，1｝表示空间相关性程度由弱到强的变动，本研究假设误差项呈正态分布，斜率系数和截距系数估计量Monte Carlo模拟结果分别如表1和表2。
由表2，在截距系数
估计量的RMSE表现上，类似于
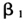的估计量，OLS估计量仍然存在较大偏差，等权重GMM-GLS估计量和最优权重GMM-GLS估计量与GLS估计量非常接近，尤其是最优权重GMM-GLS估计量，其RMSE仅比GLS估计量大3%左右；存在随机效应比不存在时RMSE有所上升，但最优权重GMM-GLS估计量与GLS估计量差距缩小至2%左右；当空间相关性较小时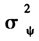（=0.25），各估计量的RMSE都低于平均RMSE，估计量更为有效；此外，各估计量的RMSE随N或T的增大明显变小，表明样本量的增大使得模型参数估计的有效性提高。由Monte Carlo模拟实验可知，本文针对面板数据SEC模型提出的GMM估计法是有效的估计方法，尤其是最优权重GMM-GLS估计量，其参数估计值的RMSE与采用误差项方差真实值的GLS估计法十分接近。接下来，本文通过实例分析研究面板数据SEC模型及其GMM估计法在实证研究中的应用。
4经济增长中要素弹性修正实例分析
关于我国经济增长中人力资本、物质资本等主要生产要素的作用，学者们做了大量研究。考虑简单的柯布一道格拉斯模型时，物质资本弹性一般都远远高于人力资本弹性。李从欣等[17]利用2001年～2005年全国省级面板数据进行分析，得出物质资本和人力资本弹性分别为0.986和0.332；董亚娟[18]研究浙江省1978年～2004年经济增长数据，得到物质资本弹性和人力资本弹性分别为0.757和0.243；吕国宁[19]分析了新疆省1990年～2006经济增长数据，得到物质资本和人力资本弹性分别为0.834和0.094。
考虑到人力资本对中国经济增长贡献的现状，上述研究中人力资本弹性在一定程度被低估，众多学者通过改进模型对此进行修正。吴玉鸣等[20]引入SEAR和SLAG模型，发现未考虑空间相关性之前，中国区域工业生产中物质资本弹性和人力资本弹性分别为0.922和0.218，考虑SEAR及SLAG后变为0.919，0.219及0.904，0.262，人力资本弹性略有提高；傅晓霞、吴利学[21]采用随机前沿模型，分析1990-2004年的省级面板数据，得到物质资本弹性和人力资本弹性分别为0.688和0.325，有效修正了经济增长中的要素弹性。中国经济运行中存在显著的空间相关性，且经济的冲击并非都存在空间溢出效应，本文采用SEC模型对各要素弹性进行修正，更符合中国经济运行的现实状况。
本文采用2000年～2007年中国30个省（西藏没有能源消耗的统计数据）的GDP、物质资本、人力资本及能源消耗的面板数据。数据来源于《中国统计年鉴》（2001～2008）、《新中国五十年统计资料汇编》、《中国能源统计年鉴》（2001年～2008）及国家统计局网站。其中，实际GDP以2000年为基年，采用GDP平减指数调整；本文的物质资本存量测算以张军等（2004）[22]22估算的省级物质资本存量数据为基础，转换为以2000年为基年的物质资本存量，同时，借鉴张军等[22]测算的固定资产折旧率（9.6%），采用永续盘存法估算出以2000年为基年的历年实际物质资本存量；对人力资本存量的估算，采用张琦（2007）[23]的教育年限法，即人力资本存量=从业人员×平均受教育年限，平均受教育年限由文盲、小学、初中、高中及大专以上的人数比例折算，各学历水平的受教育年限分别设为0、6、9、12和16年；能源消耗统一采用标准煤折算。
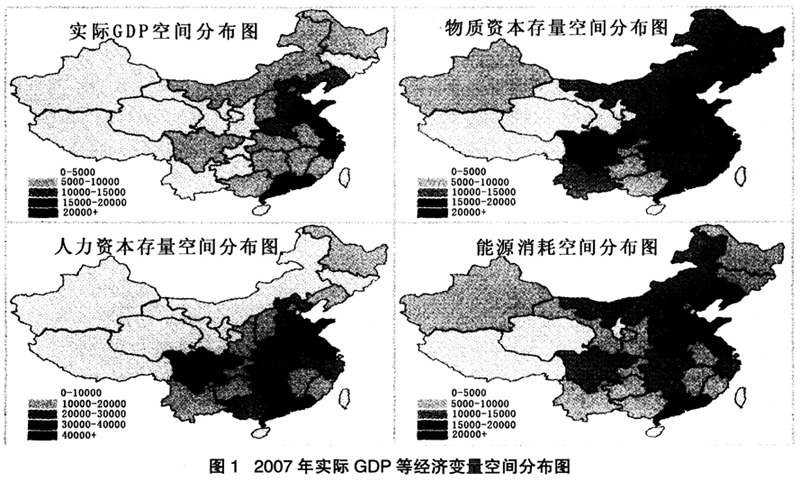
首先，本研究考察文中涉及的实际GDP等经济变量的空间分布规律，以2007年为例，如图1所示。由图1可见，各地区的实际GDP区域分布存在一定程度的空间集聚性，实际GDP在5000元以下的区域主要集中在西北和西南地区，实际GDP在5000～10000之间的区域主要集中在中部地区，而实际GDP最高的区域主要集中在山东、江浙及广东等东部及东南沿海地区。物质资本存量、人力资本存量及能源消耗也具有类似的空间分布特点，经济变量数值相近的省区在地理区位上往往也处于相邻区域，体现出经济变量之间显著的空间相关性。
直观的空间分布图体现了实际GDP等经济变量的空间集聚性。为进一步考察经济变量的局部空间相关性，研究某一地区经济对其邻近地区经济的影响，本研究利用Moran散点图进行分析，如图2。以实际GDP为例，横轴为各地区实际GDP数值，纵轴为其邻近地区的实际GDP加权值，代表该地区邻近地区实际GDP的平均状况。第一到第四象限分别表示“高—高”、“高—低”、“低—低”和“低—高”区域，其中“高-高”区域表示经济变量数值大的区域其邻近区域相应的变量数值也较大，其他区域类似定义。
由图2，各地区实际GDP的散点分布区域主要集中于Moran散点图的高—高和低—低区域，仅有6个点（20%）处于此两区域之外，仅有2个点（6.6%）远离高—高和低—低区域，表明经济发达地区能带动周边地区的经济发展，而经济落后地区阻碍周边地区经济发展。此外，各地区物质资本存量、人力资本存量的Moran散点图也呈类似的空间分布特征，主要集中在高—高和低—低区域。Moran散点图表明本研究中各经济变量均存在较显著的空间相关性。
为了进一步考察各经济变量的全局空间相关性，进行SEC模型估计之前，对本研究中各经济变量的进行空间相关性的Moran I检验（表3）。
由表3，各经济变量的空间相关性全域Moran I检验均在5%的显著性水平下拒绝原假设，表明物质资本存量等经济变量存在显著的空间相关性，模型中需要引入空间相关性分析。
本研究采用如下面板数据SEC模型：
本研究中采用可行GLS估计法对模型（16）进行估计，对误差项方差
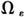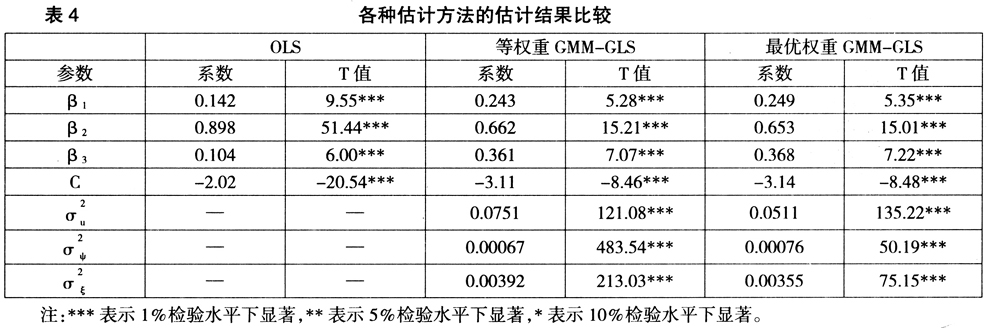
分别采用等权重GMM和最优权重GMM估计。研究中使用GAUSS 9.0进行模型的估计，得到结果如下页表4。从表4可以看出，各参数估计值均在1%的水平下显著。未考虑空间相关性的OLS估计，物质资本的弹性为0.898，人力资本的弹性和能源消耗弹性分别为0.142和0.104，物质资本的贡献远远高于人力资本和能源消耗，与吕国宁[19]等的结论基本一致。进一步，考虑空间相关性，使用面板数据SEC模型，采用等权重GMM-GLS方法和最优权重GMM-GLS进行估计，
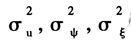的系数估计值均非常显著，表明面板数据模型中存在显著的空间相关性和随机效应，佐证了本文采用面板数据SEC模型的正确性。实证结果显示，与OLS估计相比，GMM-GLS估计的人力资本和能源消耗弹性大大提高，物质资本弹性则显著降低，这表明，考虑空间相关性影响之后，人力资本的跨省流动及能源的跨区域输送等因素的影响得到体现，人力资本及能源消耗对经济增长的贡献变大，因此物质资本的贡献则相应的减少。可见，面板数据SEC模型估计结果更加符合我国经济运行现实。5结论
为克服极大似然法在SEC模型估计中运算的困难，本文提出基于等权重GMM、最优权重GMM的可行GLS估计方法在面板数据SEC模型中的应用，证明了估计量的一致性，并通过Monte Carlo模拟实验证实了估计量在有限样本下的有效性。最后，通过实例分析说明，研究对象存在空间相关性的经济冲击情形下，采用SEC模型更适合于现实经济运行分析。本研究提出的面板数据SEC模型估计方法，有助于空间经济分析应用范围的扩大。在固定效应设定下的面板数据SEC模型估计方法及其性质，是本文进一步研究的课题。
附录
附录1矩条件的推导及定理一证明
证明因为Γ为常数矩阵，因此，Γ=O（1）且G*=Γ。
定理1证明
附录2Ξ的推导及定理二证明
参考文献：
[1]Anselin L. Spatial Econometrics: Methods and Models[M]. Dordrecht: Kluwer Academic, 1988: 7-133.
[2]Cliff A, Ord J K. Spatial Processes: Models and Applications[M]. London: Pion, 1981: 1-229.
[3]Anselin L. Rao's score test in spatial econometrics[J]. J. Stat. Plan. Inference, 2001, (97): 113-139.
[4]Lee L F. Asymptotic distributions of quasi-maximum likelihood estimators for spatial autoregressive models[J]. Econometrica, 2004, 72(6): 1899-1925.
[5]Kelejian H H. Prucha I. A generalized spatial two atage least squares procedures for estimating a spatial autoregressive model with autoregressive disturbances[J]Journal of Real Estate Finance and Economics, Econometric, 1998, 17(1): 99-121.
[6]Kelejian H H, Prucha I. A generalized moments estimator for the autoregressive parameter in a spatial model[J]. International Economic Review, 1999, 40(2): 509-533.
[7]Kapoor M, Kelejian H H, Prucha I. Panel data models with spatially correlated error components[J]. Journal of Econometrics, 2007, 140: 97-130.
[8]Kelejian H H, Robinson D P. A suggested method of estimation for spatial interdependent models with autocorrelated errors, and an application to a county expenditure model[J]. Papers Region Science, 1993, 72(3): 297-312.
[9]Kelejian H H, Robinson D P. Spatial correlation: A suggested alternative to the autoregressive model[A]. In: Anselin L, Florax R J(eds). New Directions in Spatial Econometrics[C]. Berlin: Springer, 1995: 75-95.
[10]Kelejian H H, Robinson D P. Infrastructure productivity estimation and its underlying econometric specifications: A sensitivity analysis[J]. Papers in Region Science, 1997, 76(1): 115-131.
[11]Baltagi B H. Econometric Analysis of Panel Data[M]. New York: Wiley, 2001: 1-150.
[12]Matyas P Sevestre. The Econometrics of Panel Data[M]. Berlin: Springer, 2008: 625-660.
[13]GreeneW.费剑平译.计量经济分析(第五版)[M].北京：中国人民大学出版社，2007：509-569.
[14]P
tscher B M, Prucha I. Dynamic Nonlinear Econometric Models, Asymptotic Theory[M]. Berlin: Springer, 1997: 15-31.[15]HansenL P. Large sample properties of generalized method of momernts estimators[J]. Econometrica, 1982, 50(4): 1029-1054.
[16]Das D, Kelejian H H, Prucha I. Finite sample properties of estimators of spatial autoregressive models with autoregresaive disturbances[J]Papers Region Science, 2003, 82: 1-26.
[17]李从欣，李国柱，韩宇.区域人力资本与经济增长研究[J].当代经济管理，2008，30(4)：42-44.
[18]董亚娟.人力资本对经济增长绩效的实证研究——基于浙江省的分析[J].商业经济与管理，2007，185(3)：33-39.
[19]吕国宁.人力资本与区域经济增长的相关性分析[J].科技信息，2008，28：197-198.
[20]吴玉鸣，李建霞.中国区域工业全要素生产力的空间计量经济分析[J].地理科学，2006，26(4)：385-391.
[21]傅晓霞，吴利学.技术效率、资本深化与地区差异——基于随机前沿模型的中国地区收敛分析[J].经济研究，2006，10：52-61.
[22]张军，吴桂英，张吉鹏.中国省际物质资本存量估算：1952-2000[J].经济研究，2004，10：35-44.
[23]张琦.我国人力资本存量的测算[J].统计与决策，2007，233(3)：35-36.
[24]Jennrich R. Asymptotic properties of non-linear least squares estimators[J]. The Annals of Mathematical Statistics, 1969, 40(2): 633-643.^