为了研究上述问题,对各种发展战略和经济政策可能产生的效果(包括宏观经济效果和对各产业部门的影响)进行事前的定量分析,为有关部门决策提供依据,我们研制了中国宏观经济多部门动态模型MUDAN(模型英文名称MUltisectoral Development ANalysis的简写)。
MUDAN模型是一个宏观经济多部门动态模型,它将投入产出模型特别适合于模拟经济结构变动效果的特点和总量计量经济模型的动态特点有机地结合在一起,既可用于宏观经济分析,更重要的是可将这种分析深入到产业部门一级,研究各种经济政策和外部环境变动对各产业部门的影响。
一、多部门动态模型
1.什么是多部门动态模型
多部门动态模型是一种将投入产出模型特别适合于模拟经济结构变动效果的特点和总量计量经济模型的动态特点有机地结合在一起的模型技术。多部门动态模型既是部门间联系模型,同时也是宏观经济模型,在此类模型中既确定分产业的各类变量值,同时也确定所有宏观经济变量,如GDP、收入、储蓄、就业、财政赤字、通货膨胀率等等,模型的因果关系是从部门分量到宏观经济总量。
对多部门动态模型的研究始于60年代末期,这类模型中最著名的是英国剑桥大学的MDM模型和美国马里兰大学的产业预测模型(INterindustry FORecasting at the University of Mary land,简称INFORUM模型)。MDM模型是在诺贝尔奖金获得者理查德·斯通(R.Stone)教授领导研制的剑桥增长模型(CGP)的基础上研制的第二代剑桥模型,由特端·巴克尔(Terry Barker)领导研制,是目前英国最有影响的经济模型之一。INFORUM模型是在克劳帕尔·阿尔蒙(Clopper Almon)教授领导下研制的,该模型不仅在美国拥有包括政府机构和企业在内的众多用户,而且连接了奥地利、法国、意大利、韩国、墨西哥、波兰、西班牙、日本、加拿大、俄罗斯、英国和美国等十几个国家的模型,构成了INFORUM国际系统,各国模型使用共同的软件,通过进、出口方程相连。自1993年起,INFORUM系统每年召开一次年会。第一次年会在法国召开,会上各国模型研制者交流了模型研究和应用的经验,学习如何使用新改进的模型软件,讨论各国模型的连接问题。在这次年会上,与会者以MUDAN为例,学习如何使用新的软件。
2.多部门动态模型的特点
多部门动态模型的构模有以下几个原则和特点:
(1)这类模型用行为方程描述消费者、生产者和其他经济决策人的行为,并且这些行为方程是按部门估计的。
(2)模型中使用显式的投入产出关系式。这保证了生产方的最终需求、中间使用和产品产量之间绝对的核算一致性,也保证了价格方的产品价格、所用原材料费用和产生的增加值之间绝对的核算一致性。因此,每一产业部门的活动都以一种一致的方式和经济的其他部分相联系。
(3)模型是动态的,投入产出系数逐年变动,投资依赖于产出的增长率。
(4)模型追踪经济随时间的发展,并可有限地显示经济周期。它并不着眼于某个未来时点的均衡状态,也不规定通向均衡的路径。
(5)模型既确定分产业的各类变量值,也产生宏观经济总量,如国内生产总值、收入、储蓄、就业、通货膨胀等,总量由产业一级的变量汇总得到,而不是先得到总量再将其分配到各产业中。模型的因果关系是从部门分量到宏观经济总量。
多部门模型的上述特点使它成为有别于其他类型模型的特殊一类模型。为阐明这一点,我们简要说明一下几类主要模型和多部门动态模型的区别。
传统的计量经济模型极少或根本不使用投入产出表,而是着重依靠回归分析,甚至产业部门的产出和最终需求总量相联系也是靠回归分析。而多部门动态模型则在计算分部门产出和分部门价格中都使用变动系数的投入产出表。
传统的投入产出模型极少或根本不使用以回归为基础的行为方程。在动态投入产出模型中,投资基于未来增长的“需要”,而不是基于对企业实际决定投资的方式的任何研究。这种按“需要”决定投资的方法往往导致严重的不稳定问题。而多部门动态模型则注重行为方程,特别是消费、投资、出口、进口、生产率、利润和工资等行为方程的使用。这种用行为方程来决定投资的方法彻底消除了动态投入产出模型的非经济不稳定性,而引进了一种可以说是经济周期波动的东西,这种波动事实上是可以观测到的。
可计算一般均衡模型(CGE模型)注重的是经济均衡点,而不是一国经济的动态发展过程,在此过程中,可能会呈现经济周期,但可能任何时刻都不处于“稳态”或均衡。多部门动态模型则注重于经济的动态发展过程,它产生的是经济的一个时程的预测,而不是“均衡”点之间的差异。
总量驱动的投入产出模型(如DRI投入产出模型)与多部门动态模型的主要区别是,总量驱动的投入产出模型先有总量值(可以是从一个总量模型而来),再按某种方式分解成各部门的值。而多部门动态模型则是先得到各部门分量,然后汇总成总量。显然,后者更接近于经济的实际运行,因为在实际经济中,并不存在总量驱动器,总量是由各部分之和构成的。
3.INFORUM模型系统和MUDAN模型
INFORUM模型建立于1967年,经过20多年的发展,模型已经历了三代,日臻成熟和完善。INFORUM目前有两个美国经济模型:LIFT和DOM,分别为78和420个生产部门。与此同时,INFORUM的工作由美国扩展到全世界,形成了一个包括美国、奥地利、中国、法国、意大利、韩国、墨西哥、波兰、西班牙、俄罗斯、日本、加拿大、英国和德国等十几个国家模型的INFORUM国际系统。
INFORUM系统的模型都具有共同的核算结构,使用共同的软件,因而可以很方便地联结在一起。
INFORUM模型的基本投入产出核算结构是下面两个方程组:
q=Aq+Hf p=pA+v |
其中q为产品产出列向量;A为投入系数矩阵;f为按类别的最终需求列向量;H为将按类别的最终需求转换成按产品的最终需求的桥矩阵;p为价格行向量;v是每种产品单位产出的增加值行向量。在两个方程组中的每一个向量和矩阵都应有一时间下标,它们是逐年变动的。第一个方程式是基于投入产出表中Ⅰ,Ⅱ象限的关系,第二个方程式则是基于投入产出表中Ⅱ,Ⅲ象限的关系。
f的分量可以有很多,其中包括个人消费、设备投资、存货投资、进口、出口、政府支出等。v也包括很多部分,如折旧、工资、利税、福利及其他增加值等。这些分量可以由行为方程决定,也可外生指定,各国模型可根据实际情况灵活掌握。对于一个新模型,它们可以全部是外生指定。而对于一个成熟的模型,行为方程可能相当复杂。行为方程中函数的形式也是由各国构模者自行决定的,没有统一的模式,采用的估计技术也可不同。投入产出表的部门多少和基年定为哪一年,各国模型也不必相同。因此,尽管核算结构对所有模型都是共同的,但各国构模者在构模时仍保留很大的灵活性,使各国模型具有各自的特色。
一般来说,f在投、产出表中按产品(或部门)分类,而行为方程是基于时间序列的数据,时间序列的统计资料的分类方法与投入产出表不一致,例如居民消费的统计资料是按其用途(如吃、穿、用、住、烧等)分类。仅在编制投入产出表的年份可以得到按产品(部门)分类的最终需求的数据。为解决这个问题,INFORUM采用“桥”矩阵实现按类别的最终需求数据与按投入产出表的产品(或部门)的最终需求数据的转换。
INFORUM的另一特点是从模型中内生地产生每年的价格变动,这主要体现在第二个方程组上。p是产品价格向量,则pA是单位产品的中间投入(原材料消耗)的价值,它与单位产品的增加值(v)之和就是产品的生产者价格(单位产品的生产者坐标),这种关系的数学表达式即为第二个方程组,要特别注意的是,v在实际计算中用现价的增加值除以不变价的总产出定义。在后面介绍“价格—收入模块”时还要详细介绍计算的过程。
INFORUM模型系统使用共同的软件,软件分为两个部分,其一是G回归和数据操纵程序,其作用是编制数据库、数据操纵、图形显示、执行回归并提供预测模型所需形式的回归结果。软件的第二部分是INTERDYME,这是一个建立和求解宏观经济多部门动态模型的软件包,由准备程序、模拟或预测程序和显示程序构成。
MUDAN模型是一个INFORUM类型的模型。我们之所以选择INFORUM模型作为MUDAN模型的建模模式,其主要原因是该类模型既能用于宏观经济分析,又能将这种分析深入到产业部门一级,这为产业政策的研究提供了得力的工具,能够满足“产业结构与定量分析”专题的要求。INFORUM国际系统已连接了十几个国家的模型,这些模型通过进出口方程相互联结起来,使得我们可以研究外部条件的变化对我国国民经济和产业结构的影响。如中国正在准备复关,我们可以利用MUDAN模型与INFORUM系统连接的优势在这方面作进一步的研究。此外,INFORUM模型逻辑清晰,自底向上的因果关系符合实际经济的运行模式,这些都是我们在选择模型形式时考虑的重要因素。目前,MUDAN模型已成为INFORUM系统的一个成员。
二、MUDAN模型的结构与特点
1.MUDAN模型的投入产出核算框架
MUDAN模型的基础是一个33部门的投入产出表。模型数据库使用中国1987年投入产出表和历年中国统计年鉴等资料上的数据编制而成,它包括1980-1991年部门一级的变量和宏观经济变量的年度时间序列数据。
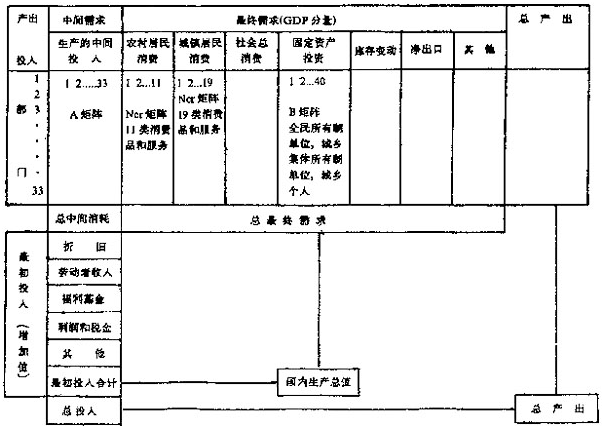
图1MUDAN模型的投入产出核算框架
图1描述了MUDAN的投入产出结构。MUDAN由三个相互关联的模块组成:生产模块、价格—收入模块和核算模块。生产模块决定不变价分部门最终需求、中间投入、产出、劳动生产率和就业。价格—收入模块计算每个产业的名义工资、利税、福利基金、其它最初投入和各种价格指数。核算模块将各产业的最终需求和收入加总编制国民核算总表,用诸产品价格的加权平均和得出各种总量价格,由增加值信息计算城镇和农村居民收入和政府财政收入,决定名义GDP等等。模型通过规定生产模块、价格—收入模块和核算模块变量之间的关系而闭合。
2.生产模块
在生产模块中,计算出分部门的各类最终需求,然后将这些最终需求代入投入产出方程得出分部门的总产出。总产出求出后,再计算分部门的劳动生产率和就业人数。
利用消费函数分别计算城镇居民对19类消费品和服务的消费,及农村居民对11类消费品和服务的消费。这些消费函数的因变量是每类消费品的人均消费额(不变价格),解释变量是实际人均收入以及该类消费品的相对价格。这些消费需求通过消费桥矩阵MCR和MCU转换成按I-O部门的居民消费需求。
按投资部门的投资(全民所有制单位投资外生,城乡集体所有制单位和城、乡个人投资内生)也通过投资桥矩阵(B矩阵)转换为对投入产出部门的投资品需求。然后居民消费、投资、出口、社会总消费和库存变动加在一起,给出没有减去进口的最终需求。这一最终需求进入投入产出方程的赛德尔迭代求解过程,进口和产出被联立地计算出来(某产品的进口依赖于对该产品的总需求,这在赛德尔迭代过程的每一步都是知道的)。然后计算出的进口再从最终需求中减去。
将它们加总以构造向量fd对每个I-O部门的总最终需求。矩阵方程为:
fd=MCR×cr+MCU×cu+Pub+B×Capital+Vin+Export-Imp+Othdm |
其中:MCR=33×11为农村居民消费桥矩阵;cr=11×1为按消费品种类的农村居民消费向量;MCU=33×19为城镇居民消费桥矩阵;cu=19×1为按消费品种类的城镇居民消费向量;Pub=33×1为社会总消费向量;B=33×40为投资桥矩阵;Capital=40×1为按投资主体的投资向量;Vin=33×1为库存变动向量;Export=33×1为出口向量;Imp=33×1为进口向量;Othdm=33×1为其它最终需求向量。
分部门产出由投入产出方程计算:
q=A×q+fd |
其中:q=33×1为不变价格部门产出向量;A=33×33为中间需求矩阵;fd=33×1为不变价格最终需求向量。
根据由于行为方程产生的部门生产率和各部门的产出水平,可以得到各部门的就业人数。
在生产模块中,除上述部门分量外,还计算两个总量,其一是不变价国内生产总值,它等于各部门最终需求之和;其二是总就业人数,它等于各部门就业人数之和。
3.价格—收入模块
价格—收入模块决定每个部门的最初投入(增加值),并由此计算部门价格指数及其它价格指数。每个部门的增加值有5个分量:劳动者收入、福利基金、利润与税金、其它最初投入和折旧。为计算各部门劳动者收入(工资),为每个部门外生地设定一个名义工资率指数序列。由生产模块得到的职工人数与工资率得到劳动者收入。
下一步是计算利税、福利基金、其它最初投入和折旧。产出利税率是外生政策变量,它乘以用上一年的产出价格指数减缩后的不变价产出,即得出每部门的利税额。每部门的福利基金是该部门的工资的函数。其它最初投入(OVA)计算方法与利税类似。初始的产出OVA率也是一个外生政策变量。在前两次迭代以后的迭代中,OVA比例因子按就业人数与劳动力的比率进行修正。折旧是产出的函数。
上述五个增加值分量之和即为各部门的增加值:
Va=Wages+Welf+Bentax+Othva+Dep |
其中,Va=33×1为增加值向量;Wages=33×1为工资向量;Welf=33×1为福利基金向量;Bentax=33×1为利润的税金向量;Othva=33×1为其它最初投入向量;Dep=33×1为折旧向量。
各部门单位增加值等于其增加值除以不变价的产出。这些量得出后即可根据下面的价格恒等式决定各部门产品的价格:
Prices=A'×Prices+Unitva |
其中:Prices=33×1为价格向量;A'=33×33为中间消耗矩阵的转置;Unitva=33×1为单位增加值向量。
价格也是通过一个赛德尔迭代循环决定的。
得到各部门的价格后,下一步就是根据这一基础价格计算各种价格指数,包括GDP平减指数,投资价格指数,农村居民消费品分类价格指数,城镇居民消费品分类价格指数,农村居民总消费价格指数,城镇居民总消费价格指数。
4.核算模块
MUDAN模型中,核算模块的功能尚不完善,还不能做到利用计算出的数据编制国民核算总表。目前采取简化处理,主要完成以下工作:
(1)确定农村居民人均收入和城镇居民人均收入。
(2)由利润和税金确定政府财政收入。
(3)根据各产品价格,确定GDP平减指数、农村居民总消费价格指数和城镇居民总消费价格指数。
(4)计算名义GDP。
5.A矩阵和各类桥矩阵的调整
模型中所使用的投入产出表的基年是1987年,该表的A矩阵中系数反映的是1987年的中间消耗情况。实际上,由于技术变革等原因,这些中间投入系数(技术系统)是逐年变动的。消费桥矩阵和投资桥矩阵的元素也是如此。因此有必要对其他年份特别是预测期各年的A矩阵和各类桥矩阵进行调整。在MUDAN模型中,这种调整采用的是阿尔蒙教授提出的“整行系数变动法”(Across-the-row coeffient Changes)。
我们一方面用产出、出口和进口的历史数据,可计算出每种产品各年的国内使用额,记为domuse,另一方面利用投入产出关系式,我们可以计算每种产品的常系数国内使用额(即A矩阵和各桥矩阵系数各年不变,均采用1987年系数计算所得到的各年每种产品国内使用额)记为u,domuse和u这两个向量的对应元素之比率称之为“整行比例因子”。然后将矩阵A、MCR、MCU和B的每一行以及向量Pub、Vin、Othdm的每个元素乘相应的比例因子。
乘上比例因子后,各桥矩阵的各列之和不再等于1,还必须经过正规化处理后才能使用。
各部门整行比例因子的历史序列,是调整预测期各年A矩阵的各类桥矩阵的依据。预测期各年的各部门比例因子,是根据它们历史的趋势,再加上专家的判断用外推法得到的。
6.模型中的实际和名义制动器
经济的发展无疑受到各种因素的制约,如自然资源和人力资源的制约,宏观经济模型必须反映这一现实。
在美国经济模型中,基本的实际制动器是劳动力,名义制动器是货币供给。在经济繁荣时,就业增加,趋近相对固定的劳动力供给;失业减少;工资和利润向上冲;价格上升;对于给定的货币量,货币变得趋紧,从而抑制通货膨胀。在经济衰退中,相反的情形发生,减缓经济的下跌。
我国正处在向社会主义市场经济过渡的时期,目前与上述过程相对应的是什么还不很清晰。但是,从近些年的经济现象看,当经济发展速度快时,农村剩余劳动力流入城市产业,当经济增长放慢时,又出现民工流回农村的现象。因此,我们在MUDAN模型中,选择劳动力作为实际制动器,但具体作法与美国模型不同。考虑到我国的实际情况,我们构造了一个“劳动力”变量,该变量的历史值取历年的总就业人数,其未来值则是用时间趋势预计的。
在选择名义制动器方面,也存在着一定的困难。
由于我国正处于过渡时期,政府进行宏观经济管理的手段正在从完全的行政性计划手段向间接调控手段改变,但是还不能象在美国等成熟的市场经济国家那样,利用货币政策来调控经济的冷热程度,所以我们不能选择货币供给或信贷规模作为名义制动器。鉴于这种情况,我们目前在MUDAN模型中通过外生地给出每个产业的名义工资率的方式,提供了一种名义制动装置。
那么,在模型中劳动力作为实际制动器是如何作用的呢?当模型中产生的就业人数超过劳动力人数时(反映的是经济过热),则其他最初投入被放大,通过乘上一个大于1的比例因子(总就业人数/劳动力总数),这意味着高利润。这一项放大,使得单位产出增加值增大,从而使得价格上升,实际收入下降,对经济过热起到抑制作用。反之,如果模型中产生的就业人数低于劳动力人数(意味着衰退),则调整的过程正好相反。
模型加上了上述名义和实际制动器后,稳定性大大增强。实际运行中,比例因子在0.5到2.0间变动,得到的其他最初投入序列相当平滑。
除上述制动装置外,在模型中还采取了另一项增强模型稳定性的措施,即在模型运行过程中,得到的有些部门的生产率增长速度过快,似乎难以为继。因此,如果任一部门的生产率年增长超出5%话,则超过5%的部分被人为地压缩,自没有历史数据的第一年起,每年压缩10%。
7.MUDAN模型的迭代求解过程
模型用迭代求解过程求解,MUDAN在一年中的计算循环如图2所示。
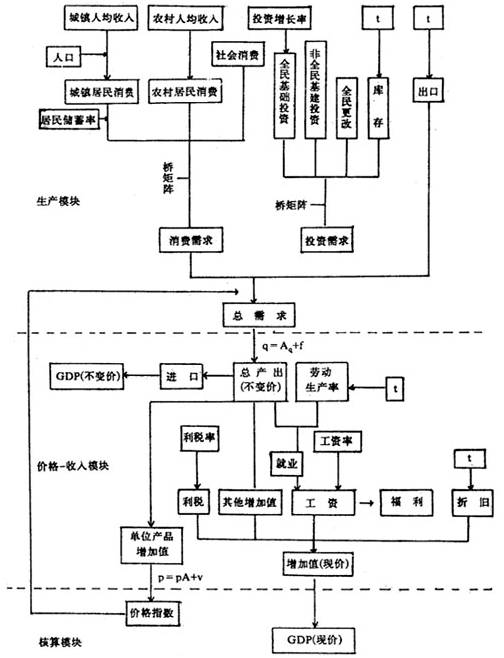
图2MUDAN模型的迭代求解过程
第一步是对投入产出矩阵A、农村居民消费桥矩阵MCR、城镇居民消费桥矩阵MCU和投资桥矩阵B进行整行系数调整。
第二步从设定一组按不变价格计算的农村居民人均收入、城镇居民人均收入和GDP的初始值开始,同时假设两组(农村、城镇)按商品种类划分的商品价格的初始值,在没有历史数据的年份,这些初始值均取前一年的数据。
第三步进行生产模块的赛德尔迭代,计算出不变价的产出和就业,再进行价格—收入模块的赛德尔迭代计算出各类价格指数。最后经核算模块得到城、乡居民的平均收入、按商品类划分的商品价格指数及GDP名义值等。
第四步以第三步计算中产生的GDP实际值与初始值进行比较,如果不收敛,则用第三步产生的结果作为初始值,从第二步开始进行下一轮的迭代计算;如果收敛,则回到第一步,用第二步计算中产生的价格指数和实际收入作为下一年计算的初始值,进入下一年的计算。
三、MUDAN模型的应用与改进
经济模型的研制与改进是一个长期的过程。经济模型是对经济运行规律应用数学与技术手段(计算机技术及其他)进行描述,借以进行经济预测或政策分析。由于人们对客观规律认识的限制,数学方法与技术手段的限制,及数据支持程度的限制,任何模型都需要不断的维护和改进才能实现其价值,模型的维护与改进有多方面,一是随着人们对经济运行规律认识的深化,对模型进行修改;二是经济运行机制本身也不是一成不变的,特别是我国正处在由计划经济向社会主义市场经济过渡阶段,经济运行机制也在不断地变化,模型研制者要不断把经济实际的变化反映到模型之中;三是数学方法的进步,新的计算软、硬件的改进,及数据情况的不断改进,也为模型的改进提供了帮助;四是不断扩展模型的功能和应用范围,在应用中求得改进和发展。国际上比较著名的模型都有一个强有力的模型研制组倾注了几十年的心血不断地进行维护和改进。INFORUM系统也不例外,它是自1967年起开始建模,经过20多年的努力,发展成今天的规模。
MUDAN模型的研制工作开始于1991年初,1992年底MUDAN的第一版调试成功,1993年6月完成第二版的调试,1994年6月开始第三版的调试。第三版在两个方面作了改进,一是将原有的33个部门投入产出分析,扩张为63个部门,即把原来投入产出表中的工业部门由23个扩展为40个,把运输业细化为4个部门。二是通过进、出口方程、实现了与INFORUM其他成员国模型的连接。第三版的调试工作仍在进行中。
我们用MUDAN模型(第二版)对中国未来15年的经济发展与产业结构变动趋势进行了预测,其计算结果与分析请见另文。
