面板数据计量模型适应性的比较研究（一）

内容提要：近年来在经济管理研究中采用面板数据的实证性论文日益增多，同时关于面板数据处理的理论成果也并不少见。然而，问题在于：一方面已有的关于面板数据处理的理论方法多基于无穷大样本，而现实中仅能获得有限样本；另一方面已有的实证研究成果或对面板数据不做任何特殊处理或并不说明处理方法选用的依据。基于此，按只存在个体效应，只存在时间效应和同时存在两种效应3种不同的数据结构，模拟比较了现有各种理论方法的适用性。并根据各种处理方法在小样本情况下估计结果存在较大差异这一事实，反推出用于判断实际数据中存在何种效应的准则。
    关键词：面板数据 固定个体效应 固定时间效应 聚类回归标准差系数
    作者简介：刘莉亚(1976- )，女，山西长治人，博士，上海财经大学金融学院副教授，博士生导师，E-mail:liuliya0112@163.com；丁剑平，上海财经大学现代金融研究中心；覃筱，上海交通大学安泰管理学院（上海200052）；代飞，上海财经大学金融学院（上海200433）。
    0引言
    众所周知，当经典计量经济模型的4个基本假设满足时，估计参数贝塔的标准差是无偏且一致有效的，但是，当不同时期的观测值与残差之间存在相关关系时，直接应用OLS回归有可能对贝塔的标准差产生有偏的估计，同时，检验贝塔参数的置信度需要构造t统计量，在贝塔标准差估计有偏的情况下，会相应地减小或增大对应的t值，从而增加估计结果出错的概率。此外，自变量和残差之间存在显著的相关关系，表明模型中还有重要的信息没有被充分挖掘，有时贝塔标准差估计甚至会产生较大偏差，甚至无法确定所建立的方程究竟是否有效。面板数据(panel data)，由于具有时间和横截面两个维度，能够很好地研究不同公司（地区）在不同时期的特征，因此近几年在实证研究中获得了广泛的应用。例如，统计了《经济研究》、《管理世界》、《金融研究》、《世界经济》等主要学术期刊中运用面板数据的论文数量，结果发现，从2002年到2008年，主要经济管理类学术刊物中运用面板数据的论文呈现出明显的上升趋势（参见图1）。
    
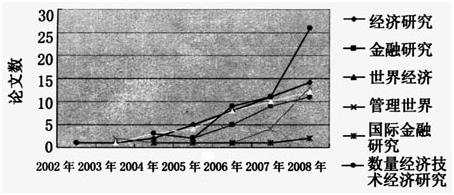
    图1近年主要学术期刊发表基于面板数据的论文数量
    越来越多的论文采用面板数据，充分说明了用面板数据研究经济问题的优点。然而，正因为此，面板数据比一般一维时间序列或横截面数据更为复杂，直接应用OLS回归，同一时期不同公司间的残差之间可能存在相关关系，同一公司不同时期的残差之间也可能存在相关关系。然而，许多论文在应用面板数据进行实证研究时，往往不考虑对贝塔标准差的调整，或者只进行了部分调整。具体来说，许多文章采用了面板数据中的固定效应模型进行研究，但是只考虑了个体效应，即只针对同一时期不同公司的残差相关关系进行了调整，很少文章考虑时间效应，这样的结果往往是不能令人信服的。本文将显示，如果没有考虑数据中存在时间效应，即使采用了固定效应模型，其估计结果也是有较大偏误的。
    下面，做一个简单的回归来说明直接应用OLS回归可能产生的错误。
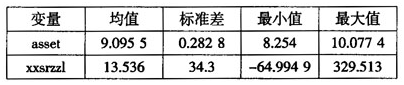
    针对上市公司成长性与规模的关系研究，本文选择销售收入增长率代表公司的成长性，选择公司总资产的对数值作为公司规模的衡量指标。并选择了商业百货上市公司（来自证监会行业分类的零售业）1997至2006年共10年的数据，为了消除异常数值的影响，又去除了带有*ST①，ST以及部分数据不全的上市公司数据，共45家公司。所有数据均来源于wind咨询。下文以asset代表资产规模，以xxsrzzl代表销售收入增长率，各变量的统计性描述见表1。
    表1各变量的描述性统计
    
    设立如下模型来分析上市公司成长性与规模的关系
    
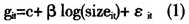
    其中，下标i和t分别表示上市公司和时间；g表示公司成长性，数据为各公司每年的销售收入增长率；size表示公司规模，数据为各公司的总资产。以上是基准模型，根据研究目的的不同，在具体的研究中会采用不同的形式。
    当直接采用OLS对上式进行回归时，β的估计值为10.325，标准差5.7101，t值为1.8083，在10%的置信水平下显著。然而，如果考虑了固定个体效应，情况就大不相同。采用固定个体效应模型估计，得到β的估计值为7.8475，标准差为9.2633，其值约为OLS估计的1.6倍，t值只有0.84716。采用固定时间效应模型估计，得到β的标准差为6.0857，与OLS估计结果差别并不大。因此，如果没有考虑固定个体效应而直接估计，那么很有可能得出的是完全相反的结果。面板数据模型扰动项可能存在异方差性、序列相关与截面相关，许多学者提出了不同的方法应用于面板数据的估计。针对固定效应模型，Kiefer[1]提出了Kiefer标准差，针对面板数据估计中残差存在序列相关的情况，该估计方法在面板数据不存在异方差的时候是稳健的。White[2]提出了针对计量模型中存在异方差的一般估计方法。在两者的基础上，Arellano[3]提出了Arellano标准差，该估计系数在存在异方差和序列相关时都是稳健的。尽管如此，Arellano系数在提出后并没有被广泛采用，可能的原因在于该估计系数在小样本情况下的有效性问题。然而，Kezdi[4]通过模拟证明了在只存在固定个体效应的情况下，只要个体数日大于50，Arellano标准差依然能够得到比较稳健的结果。
    Fama和MacBeth[5]提出了Fama-MaeBeth回归方法，该方法能够很好地处理资产价格的时间效应，因此该回归方法在资产定价的学术论文中得到了广泛应用。由于资产价格的时间序列数据也可以看作特殊的面板数据，在下文的模拟和实证分析中，也包括了文献中常用的Fama-MacBeth方法。此外，Newey和West[6]提出了Newey-West方法，并在后来被改进用于面板数据的回归分析，Driscoll和Kraay[7]提出厂Driscoll-Kraay标准差以调整面板数据中存在个体效应和时间效应时的β标准差。但是这些方法并没有得到广泛应用。
    尽管面板数据的处理在理论上有了较大的发展，但在应用上仍受到一定限制。主要原因在于理论推导是基于大样本进行的，而实际研究中人们可以得到的面板数据样本量却很小，因此，许多理论上完美的方法在实际应用中就会大打折扣，在小样本情况下，不同方法对同一面板数据的应用结果可能差别很大。但是，差别究竟有多大？各种方法分别适用何种结构的数据？这就需要采用模拟方法来回答了。本文试图通过对实证中常用的面板数据研究方法进行比较研究，通过模拟指出采用不同方法进行估计的偏误，尤其是针对运用面板数据研究中样本过小的问题，较为深入地比较在只存在个体效应，只存在时间效应和同时存在个体效应和时间效应时，各种方法在小样本情况下的估计结果。结果表明：在数据中存在不同的效应时，运用不同的方法会产生较大差异的结果。然而，这也提醒人们，在产生较大差异时，需要注意数据中可能存在着某一类型的效应。
    13种不同情形下面板数据处理方
    法在有限样本下的比较分析
    在实际的面板数据中，常常有3种类型的因素影响残差的相关性。Hsiaoa[8]把它们称为个体时期恒量(individual time-invariant)，时期个体恒量(period individual-invariant)和个体时期变量(individual time-varying)。在存在个体时期恒量(individual time-invariant)的情况下，某个公司在不同时期的残差可能是相关的，伍德里奇把它称为不可观测个体效应(unobserved firm effect)；在存在时期个体恒量(period individual-irwariant)的情况下，某个时期不同公司之间的残差可能是相关的，伍德里奇把它称为不可观测时间效应(unobserved time effect)；另外，不同公司在不同时期的残差可能存在相关关系，这叫做不可观测个体时间效应(unobserved firm-time effect)。
    正因为面板数据受到多种因素的影响，针对不同的影响因素，计量经济学家提出了不同的方法对贝塔的标准差进行调整。最常用的有Arellano[3]在Kiefer[1]、White[2]等人的基础上引入聚类回归分析(cluster analysis)，称为聚类回归标准差估计系数(cluster standard error estimator)，调整固定效应模型的贝塔标准差。再有，学术上在资产定价中常用Fama-MacBeth方法进行回归，该方法能够消除数据的时间效应。
    为了便于对聚类回归标准差估计系数和OLS方法进行比较②，首先简要回顾基于面板数据的OLS回归模型。一般地，面板数据的OLS回归模型可以写为
    
    
    上述OLS回归方程是建立在假设残差独立同分布的基础上的，残差独立的假设用于从第1行推出第2行，残差同分布的假设（即同方差）用于从第2行推出第3行④。OLS回归可以得到无偏的贝塔标准差。然而，正如前文所述，在面板数据中关于残差独立的假设常常被违背，下面分别考虑以下几种情形。
    1.1只存在固定公司（个体）效应
    为了放宽残差独立这一假设，本文首先假设只存在固定的个体效应，不存在时间效应，因此残差就可以写为
    
    上述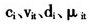都是具有零期望、有限方差的变量，并且相互独立。这样，就能保证下文模拟中对模型的系数估计结果是有效的。因为自变量和残差在同一个体中都是相关的，但是在不同个体之间是相互独立的，即
    
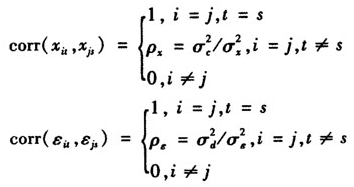
    通过上式可以看出，由于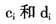的存在，OLS回归对贝塔的标准差估计是有偏的。一般来说，OLS低估了真实的贝塔标准差，并且随T的增加而增加[10]。
    1.1.1固定效应模型的估计系数
    在只存在公司固定效应时，可以用下面的固定效应模型进行回归，即
    
    而Kiefer[1]提出了下面的β标准差的估计量，该估计量在满足不存在异方差情况时是有效的。
    
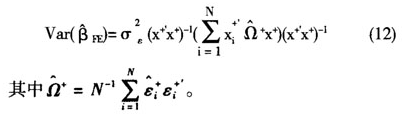
    继而，Arellano[3]提出了更广义的β标准差的估计量，即
    
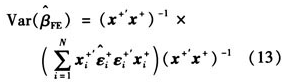
    该估计量在存在异方差或者残差存在序列相关时都是有效的。

（未完待续）