中国城市人口死亡率的预测

内容提要：死亡率是随时间变动的具有不确定性的变量，基本养老保险的养老金给付必须考虑动态死亡率的影响，因此需要对中国城市人口的未来死亡率变动进行预测。针对部分年的中国城市分性别人口死亡率数据缺失的实际状况，本文运用死亡人数服从Poisson分布的Lee-Carter模型进行了预测，结果表明该模型的拟合较好。由上述预测得出，随时间的延续，中国城市人口的预期寿命将明显增加，为基本养老保险的支付带来严重的风险，该风险导致基本养老保险个人账户的收入远不足以支付未来的养老金，必须引起重视。本文就如何规避这一风险给出了一些政策建议。
    关键词：死亡率预测 Lee-Carter模型 养老保险
    作者简介：祝伟，陈秉正，清华大学经济管理学院（北京100084）
    引言
    死亡率假设是人寿保险精算的关键假定之一，对社会养老保险的给付、人寿保险的产品定价和准备金提留等问题均有重要影响。传统的精算模型隐含假定死亡率是“静态”的：死亡率随年龄的不同而变动，未考虑死亡率在不同死亡年（即死亡的日历年）有可能是不同的。实际上，随时间的延续，死亡率改善导致的人口预期寿命的增加已经成为全球性趋势，中国人口的死亡率同样表现出明显的改善趋势：出生人口预期寿命从1990年的68.6岁增加为2005年的72.1岁[1]，死亡率变动呈现出动态性和不确定性。为更准确地计算相关养老保险计划的保费或相关给付，需要引入动态死亡率假设。对于中国基本养老保险而言，基本养老保险的养老金给付必须考虑动态死亡率的影响，因此需要对相应投保群体的未来死亡率进行预测。近年来死亡率预测模型的研究取得很大进展[2,3]，其中文献[4]基于美国人口的死亡率数据提出的Lee-Carter模型具有模型简洁、对死亡率变动拟合较好、与官方预测相比预测效果更好且可以对预测的不确定性进行分析等优点，成为死亡率预测模型研究的热点之一[5,6]，并且死亡率指标的Lee-Carter模型预测结果被美国统计局作为美国人口死亡率长期预测的一个基准[7]。中国人口死亡率预测的研究还较少，文献[8]针对1986～2002年中国分性别人口的死亡率数据（其中1987～1988年、1991～1993年和2000年数据缺失），运用Lee-Carter模型对中国人口死亡率进行估计和预测，并将预测结果与中国统计局的预测结果和实际结果进行了比较，说明Lee-Carter模型的预测结果较优。需要指出上述的研究存在一定的局限性：由于中国人口死亡率的年度数据存在缺失，针对存在缺失的数据运用奇异值矩阵分解方法估计Lee-Carter模型存在局限性[9]。针对此问题，文献[9]提出了加权最小二乘估计方法和基于死亡人数服从Poisson分布假设的极大似然估计方法，文献[10]进一步研究了极大似然估计方法的建模及应用。
    由于中国基本养老保险的覆盖范围为部分城市人口，本文采用历年《中国人口统计年鉴》中的城市分性别人口的死亡数据，运用Lee-Carter模型的极大似然估计方法给出模型参数的估计，并预测中国城市分性别人口的未来死亡率，进而结合中国基本养老保险的现状分析死亡率变动的影响，给出一些政策建议。
    一、死亡率的相关指标
    
    上述死亡率相关指标的公式均隐含死亡率仅随年龄变动，未考虑死亡率在不同日历年是不同的，即在传统的精算框架内死亡率是静态的。实际上，近年来中国人口的预期寿命显著提高，死亡率改善明显，死亡率呈现出明显的动态变化趋势。
    二、Lee-Carter死亡率预测模型
    在对死亡率变动的不确定性和死亡率变动与年龄、日历年的相关性进行考察之后，文献[4]提出了一个相当简洁的模型
    
    当存在数据缺失时，Lee-Carter模型奇异值矩阵分解的估计结果不理想。针对此问题，文献[9,10]研究了基于死亡人数服从Piosson分布的极大似然估计方法，假定死亡人数服从Piosson分布
    
    三、中国城市人口的死亡率预测
    （一）数据的预处理
    本文采用的中国城市人口的分性别年龄的粗死亡率数据源自1989年至2006年《中国人口统计年鉴》。其中，1987～1988年、1991～1993年和2000年数据缺失，该数据集有以下需要处理的问题：
    1.数据的样本不同。有些年采用的是变动抽样，有些年采用的是千分之一人口抽样，有些年采用普查数据。
    2.数据的年龄分组不同。有些日历年的死亡率数据按每1岁进行年龄分组直至100岁，有些日历年的死亡率数据按每5岁的年龄分组，大部分日历年数据的末组为90岁以上(90+)，一个日历年数据的末组85岁以上(85+)，还有部分日历年数据的末组为100岁以上(100+)。
    对于上述问题，本文处理如下：
    1.本文假定变动抽样和千分之一人口抽样具有良好的随机抽样特征，以城市年中人口为100万的基准对分性别年龄的死亡人数进行了调整。
    2.本文采用按每5岁的年龄分组的末组为90岁以上的数据作为标准数据。对按每1岁分组数据且末组为85岁以上的1996年数据先对末组数据进行了拆分后按每5岁进行了合并，对末组为100岁以上的1986，1995和2005年数据中的90～94，95～100和100+三组数据进行了合并。其中，对末组为85岁以上数据运用Human Mortality Data中数据的处理方法[13]进行了拆分（见附录）。
    （二）死亡率预测结果
    
    
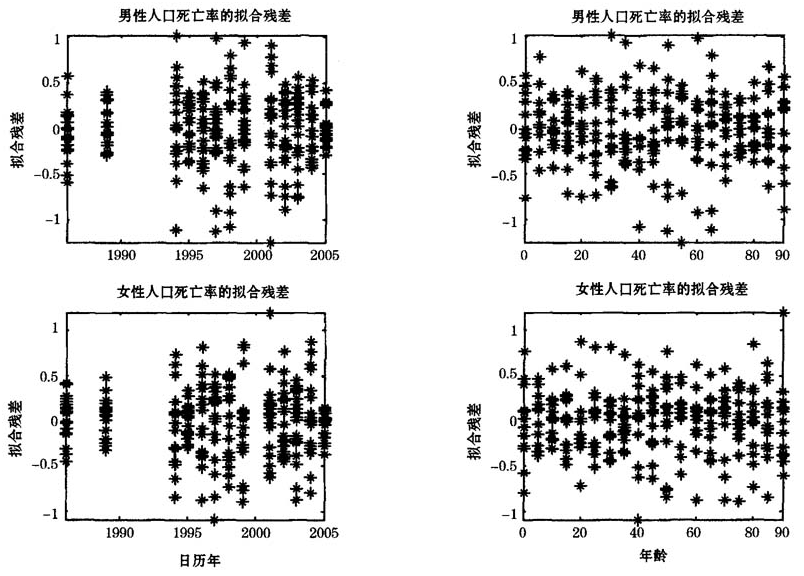
    图1Lee-Carter模型拟合的残差图
    图1中以日历年分类的残差点的绝对值较小且分布较分散，表明基于Poisson分布假设的Lee-Carter模型的拟合效果较好。本文进一步运用文献[14]给出的BDS检验方法对得出的男性和女性人口死亡人数的残差序列进行独立性检验，BDS检验方法的优点是对于残差项中存在的线性和非线性的非独立关系均具有较好的检验效力，本文的检验结果如表1所示。
    由于本文男性人口和女性人口的死亡人数的有效残差项的样本数分别为245和244，样本量较小[14]，因此本文同时给出了大样本下BDS检验统计量服从的标准正态分布的概率值和Bootstrap方法得出的有限样本下检验统计量对应的概率值。从表中可以看出，对于女性人口，BDS检验统计量对应的概率值较大，接受BDS检验的原假设，即女性人口死亡人数的残差项是相互独立的；而对于男性人口，BDS检验统计量对应的概率值较小，在5%的显著性水平下拒绝原假设，即男性人口死亡人数的残差项不独立。对此的解释是上述Lee-Carter模型估计得出的男性人口对应的残差项中可能包含较明显的出生年效应（出生年效应表示不同日历年出生的人群具有不同的死亡率变动特点。）[12]因此导致残差序列不满足独立性要求。本文应用的Lee-Carter模型考虑了死亡发生的日历年和年龄对死亡率的影响，未包含出生年效应，因此估计的残差结果可能包含一定的出生年的影响。但由于中国城市人口死亡率数据的时期较短，不具备运用包含出生年效应的模型的条件，此问题尚需进一步研究。
    表1分性别人口死亡率的拟合残差序列的BDS检验
    
    
    从图4可以看出：
    (1)伴随时间的延续中国城市人口的预期寿命明显延长。男性出生人口预期余命从1994年的70.4岁增加至2005年的75.7岁，由本文预测，将进一步增加到2015年的79.5岁；女性出生人口预期余命从1994年的74.9岁增加至2005年的80.0岁，并将进一步增加到2015年的82.3岁。
    
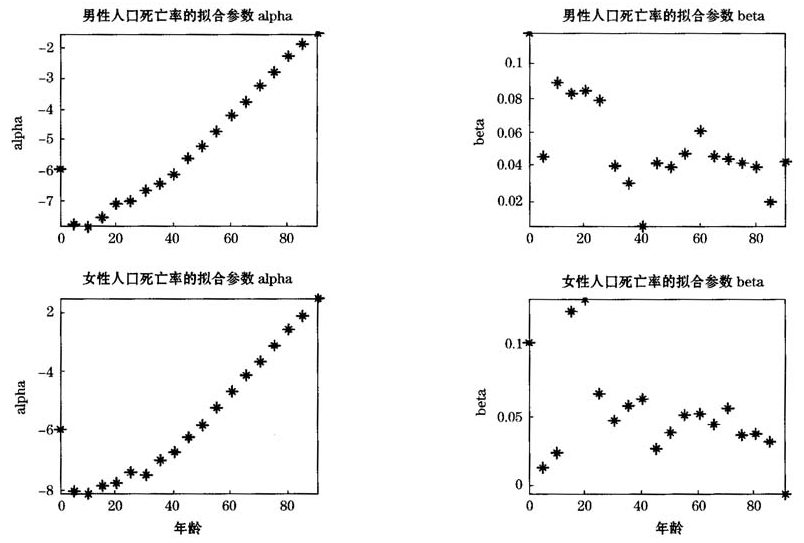
    图2Lee-Carter模型拟合值序列
    
    图3Lee-Carter模型参数的估计值和预测值序列
    
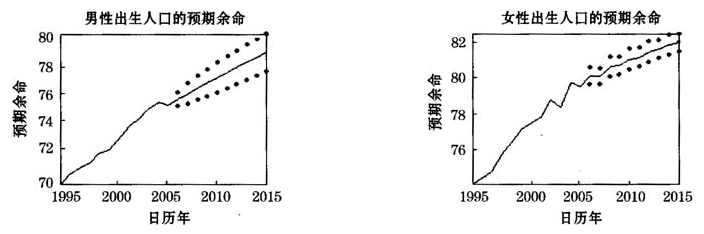
    图4出生人口预期余命实际值和预测值序列
    (2)男女相比较，在相同的日历年，女性人口的预期寿命明显高于男性。
    同样可以计算出退休人口的预期寿命，以60岁人口为例：男性60岁预期余命从1994年的16.1岁增加至2005年的19.2岁，由本文预测，将进一步增加到2015年的21.9岁；女性60岁预期余命从1994年的18.6岁增加至2005年的22.0岁，并将进一步增加到2015年的23.8岁。
    需要指出的是，有部分文献直接运用已知的人口预期寿命的时间序列预测未来的人口预期寿命，这一方法具有一定的局限性。从上文分析可以看出，人口预期寿命是一“合成”指标：综合反映了各年龄段死亡率的变动，因此仅使用这一指标本身的信息进行预测实际上未能充分利用已知信息，预测的精度和可信度存在一定局限性，这一问题在文献[4]中有较详细的讨论。
    （三）死亡率变动对中国基本养老保险的影响分析
    中国实行社会统筹与个人账户相结合的基本养老保险制度。基本养老金由基础养老金和个人账户养老金组成。依2005年国务院颁布《国务院关于完善企业职工基本养老保险制度的决定》的规定，退休时的基础养老金月标准以当地上年度在岗职工月平均工资和本人指数化月平均缴费工资的平均值为基数，缴费每满1年发给1%。个人账户养老金月标准为个人账户储存额除以计发月数，计发月数根据职工退休时城镇人口平均预期寿命、本人退休年龄、利息等因素确定。在2004年《吉林省完善城镇社会保障体系试点实施方案》中规定60岁退休人口个人账户的计发月数为139个月，依此规定，分别以不同的年利率计算，得出60岁退休人口群体的个人账户收支平衡的平均发放月数如表2所示。
    表2不同利率下60岁退休的个人账户收支平衡的平均发放月数
    
    而依本文计算结果，2005年60岁退休人口男性的预期余命约为230个月、女性的预期余命约为264个月，2015年60岁退休人口男性的预期余命约为263个月、女性的预期余命约为286个月。上述结果表明，对于2005年的60岁退休人口，未来20年的年平均实际利率（复利）要达到6%～7%，个人账户才可能实现收支平衡（由于长期的通货膨胀风险是非常严重的，实际操作中养老金计划一般会依据通货膨胀率进行指数化调整，因此在本文的讨论中使用的是实际利率）；对于2015年的60岁退休人口，需要更高的年实际利率才能实现个人账户收支平衡。而长期实际利率很难维持如此高的水平。当假定吉林省基本养老保险的保障人口的预期余命与全国城市人口的预期余命较接近时，依据上述个人账户的计发月数得出的使得退休人口个人账户支付收支平衡的发放月数可能会远小于实际需要的发放月数（本文仅列出60岁退休人口的区别，其余岁数退休人口的数据类似），基本养老保险的个人账户面临收不抵支的风险；且由于男女性的计发月数未做区分，女性基本养老保险的个人账户面临的风险更为严重。另外，由本文的预测结果，未来城市退休人口的预期余命将进一步增加。在上述方案设计中由于低估人口预期寿命所产生的支付风险将完全由基本养老保险承担，因此，由人口寿命增加所产生的养老金计划支付的风险不容忽视，人口预测作为风险度量的一项基础工作十分必要。
    四、结论
    在历年中国城市分性别年龄人口死亡率数据中部分年数据缺失，因此本文运用死亡人数服从Poisson分布假设的Lee-Carter模型对中国城市人口死亡率进行了预测。结果如下：
    (1)由模型拟合的残差图，Lee-Carter模型的拟合和预测结果较理想。
    (2)依据预测结果，中国城市人口的预期寿命将明显增加，且女性人口的预期寿命明显高于男性人口的预期寿命。
    (3)在部分省市实施的基本养老保险中，上述基本养老保险中个人账户面临由于低估保障人群的预期寿命产生的收不抵支的风险，该风险不容忽视。
    由此，本文对基本养老保险建议如下：首先，在确定个人账户的计发月数时应尽可能准确地度量人口的预期寿命，建立计发月数的定期调整机制（最好每年进行调整）：选择合适的预测方法得出未来人口的预期寿命，依据预测结果进行调整。其次，由于女性退休人口的预期寿命明显高于男性人口的预期寿命，因此在确定个人账户的计发月数应对男性和女性做出合理区分。
    附录
    
    当上述估计值小于0.25时，假定该年龄段及其上的其他年龄段的死亡人数为0。将得出的85岁以上的每岁死亡数据分为85～99和90+两组即完成拆分。
    参考文献：
    [1]中国人口统计年鉴[M].北京：中国统计出版社，2006.
    [2]Wong-fupuy C, and Haberman S. Projecting Mortality Trends: Recent Developments in The United Kingdom and The United States [J]. North American Actuarial Journal, 2004, 8 (2): 56-83.
    [3]Pitacco E. Survival Models in a Dynamic Context: a Survey [J]. Insurance: Mathematics and Economics, 2004, 35:279-298.
    [4]Lee R, and Carter L. Modelling and Forecasting U. S. Mortality [J]. Journal of the American Statistical Association, 1992, 87: 659-671.
    [5]Lee R. The Lee-Carter method for forecasting mortality with various extensions and applications [J]. North American Actuarial Journal, 2000, 14: 80-93.
    [6]Lee R, and Miller T. Evaluating the performance of the Lee-Carter method for forecasting mortality [J]. Demography, 2001, 38 (4): 537-549.
    [7]Hollmann F W, Muler T J, and Kallan J E. Methodology and assumptions for the population projections of the United States: 1999 to 2100 [R]. Working Paper 38, Population Division, U. S. Bureau of the Census, 2000.
    [8]卢仿先，尹莎.Lee-Carter方法在预测中国人口死亡率中的应用[J].保险职业学院学报，2005,6:9-11.
    [9]Wilmoth J R. Computational methods for fitting and extrapolating the Lee-Carter model of mortality Change [R]. Technical report. Department of Demography. University of California, Berkeley, 1993.
    [10]Brouhns N, Denuit M, and Vermunt J K. A Poisson log-bilinear regression approach to the construetion of projected lifetables [J]. Insurance: Mathematics and Economics, 2002, 31: 373-393.
    [11]Koissi M C, Shapiro A F, and Hogans. Evaluating and extending the Lee-Carter model for mortality forecasting: Bootstrap confidence interval [J]. Insurance: Mathematics and Economics, 2006, 38: 1-20.
    [12]Renshaw A E, and Haberman S. A cohort-based extension to the Lee-Carter model for mortality reduction factors[J]. Insurance: Mathematics and Economics, 2006, 38: 556-570.
    [13]Wilmoth J R, Andreev K, Jdanov D, and Glei D A. Methods Protocol for the Human Mortality Database University of California [R/OL]. Berkeley (USA), and Max Planck Institute for Demographic Research, Rostock (Germany),2007. http://www. mortality. org or http://www. humanmortality.de.
    [14]Brock W, Dechert D, Scheinkman J, and LeBaron B. A Test for Independence Based on the Correlation Dimension[J]. Econometric Reviews, 1996, 15 (3),197-235.