会员登录
会员注册内容提要：由死亡率下降带来的长寿风险给社会、政治以及经济带来了新的挑战。为了更加准确地对长寿风险进行评估和管理，需要对未来死亡率趋势进行预测。本文针对我国死亡率数据样本量小以及数据存在缺失的实际情况，对Lee-Carter模型进行了改进，通过一个双随机过程对Lee-Carter模型中的时间项进行建模。在模型中考虑了样本量不足对预测结果造成的影响，使得改进后的Lee-Carter模型更加适合目前中国的人口死亡率预测。
关键词：死亡率预测 长寿风险 Lee-Carter模型
作者简介：韩猛，内蒙古财经学院统计与数学学院讲师（内蒙古呼和浩特010051），中国人民大学统计学院博士研究生（北京100872）；王晓军，中国人民大学统计学院教授，博士生导师（北京100872）。
一、引言
近20多年来，人口长寿风险，即人口死亡率下降和寿命延长的不确定性，以及这种不确定性给养老和医疗保障体系带来的冲击，已成为风险管理与精算研究的热点。这一研究的最基本问题是对人口死亡率的预测。传统上，在历史数据的基础上，利用参数方法，对未来死亡率的变动做出预测。但参数方法依赖于预测者对模型和参数的主观判断和选择，没有考虑死亡率的随机波动，无法给出预测区间。
Lee和Carter(1992)在充分考虑死亡率波动的随机性以及死亡率与时间和年龄相关性的基础上，给出了一个简洁的随机死亡率模型。这一模型将对数死亡率表示为两个部分之和，一部分是和时间无关的年龄项，另一部分反映了死亡率的变化趋势，由反映死亡率整体变化趋势的时间项和反映不同年龄对死亡率变化敏感程度的年龄项的乘积组成。许多研究表明，Lee-Carter模型弥补了传统方法的不足之处，被广泛地用于不同国家人口的死亡率预测以及精算实务中。
Lee-Carter模型采用的是时间序列分析方法，一般需要二三十年的死亡率历史数据。但我国的死亡率数据十分有限，目前只有不足15年的连续年份城市人口死亡率数据，同时，人口死亡率统计数据的质量也大大限制了Lee-Carter模型在中国的应用。虽然尹莎(2006)以及祝伟和陈秉正(2009)分别利用Lee-Carter模型及其改进的Poisson log-bilnear(PB)模型对中国人口死亡率进行了预测，但他们在建模中并没有考虑样本量不足所带来的影响，从而可能造成对死亡率变动的估计不足。
二、Lee-Carter模型及其PB改进
（一）Lee-Carter模型及其PB改进模型
在经典的Lee-Carter模型中，假定对数死亡率
三、双随机过程对Lee-Carter模型时间项的拟合
如前所述，基于我国人口死亡率数据数量和质量方面的限制，在运用Lee-Carter及其改进的模型进行人口预测时，需要做适当的改进。
（一）数据说明
本文采用1994年至2005年中国城市人口分性别、分年龄死亡率数据，其中1995年的城市人口死亡率数据来自1995全国1%人口抽样调查资料，其余各年城市人口死亡率数据来自于《中国人口统计年鉴》。这些数据中，2000年的数据是人口普查数据，1995年和2005年的数据来自于1%人口抽样调查，而其余各年的数据为变动人口抽样。在年龄分组中，大部分的数据是按每5年进行分组，其中1995年、2000年和2005年的数据末组年龄为100+，而1996年数据末组年龄为85+，其余各年数据末组年龄都为90+。本文在预测中对年龄取5岁组，末组年龄取90岁，对1996年的末组数据进行拆分，对末组年龄为100+的数据进行合并，并假定变动抽样方法具有较好的随机抽样特征。
（二）参数估计
图1（见下页）是通过极大似然估计得到的男性和女性的
的拟合值。从图中可以看出，估计的参数值和实际观察到的死亡率变化趋势相吻合。图2（见下页）给出了模型的拟合残差。从图中可以看出，残差中已经没有明显的年龄和时间趋势，这表明拟合的残差基本上是独立的。从图2还可以看出，我国城市人口死亡率不包含明显的出生年效应，因此不包含出生年效应的Lee-Carter模型是适合于我国城市人口死亡率预测的。
（三）时间参数的建模
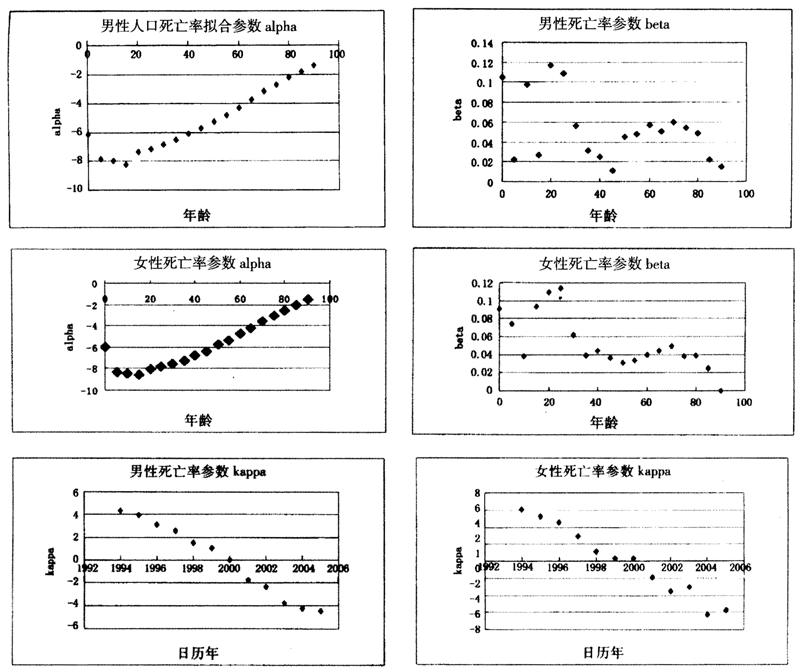
图1Lee-Carter模型参数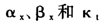
的拟合值序列
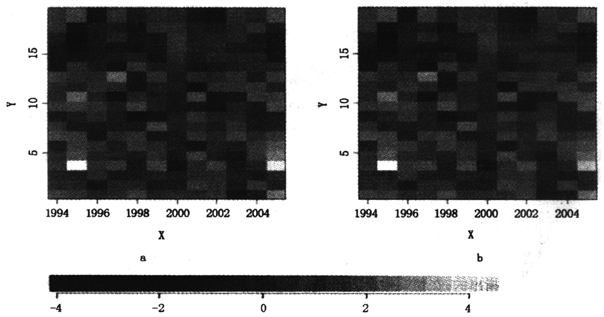
图2Lee-Carter模型拟合残差
图a－男性b－女性
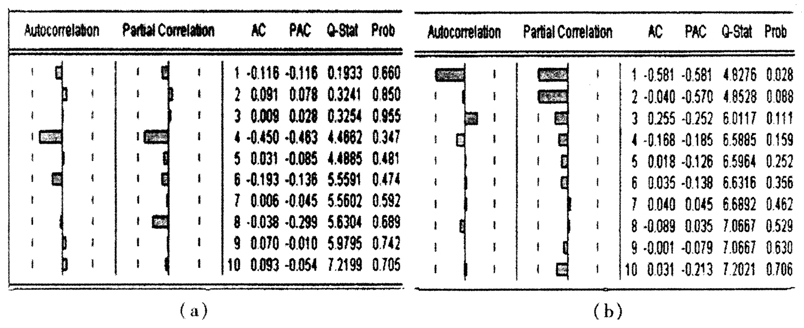
图3Lee-Caner模型中参数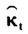
拟合值序列的平稳性检验
a－男性b－女性
相应的，本文在表1和表2（见下页）中分别给出了60岁男性和女性的预期余命，假定人的最大寿命为105岁。如同Lee和Carter(1992)指出的，在预期寿命估计中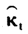
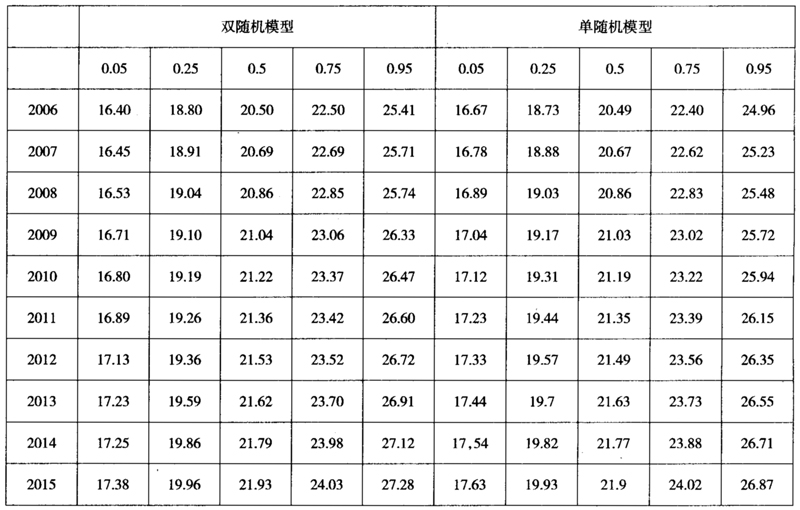
项的拟合误差占预期寿命误差的绝大部分。因此，本文仅仅考虑死亡率时间项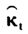
拟合的误差对预期寿命的影响，而忽略了在Lee-Carter模型建模中对死亡率数据拟合所产生误差的影响。从表1可以看出，60岁男性预期余命将会从2006年的20.5岁增加到2015年的21.93岁，而60岁女性预期余命将会从2006年的22A2岁增加到2015年的23.58岁。
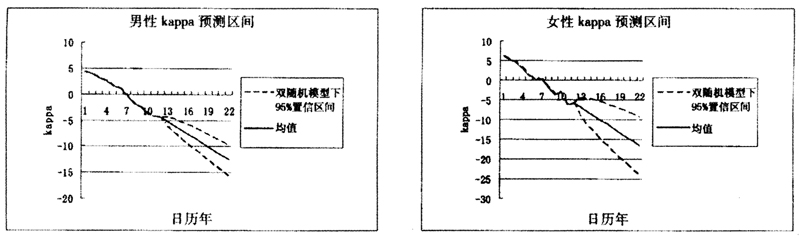
图4Lee-Carter模型参数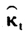
预测值和置信区间（置信度为95%）
表160岁男性预期余命及置信区间
（四）死亡率下降对我国企业职工基本养老保险的影响
根据2005年国务院颁布的《国务院关于完善企业职工基本养老保险制度的决定》的规定，个人账户养老金的计发标准以个人账户存储额除以计发月数，其中计发月数是根据退休时城镇人口预期寿命、个人退休年龄以及利率等因素确定。而目前大多数省份规定60岁退休职工的个人账户计发月数为139个月。而依据本文的计算结果，2005年60岁退休男性的预期余命为246个月，女性为267个月，而到2015年60岁退休男性的预期余命为263个月，女性为284个月。这表明对于2005年60岁的退休人口而言，要实现个人账户的收支平衡，不考虑通货膨胀的情况下，账户的收益率至少需要达到6%至7%，对于2015年的60岁退休人口而言，可能面临着更加严峻的形势。对于企业职工基本养老保险而言，长寿风险不能忽略，死亡率预测作为长寿风险度量的基本工具非常重要。
表260岁女性预期余命及置信区间
四、结论
在历年中国死亡率数据比较少的情况下，本文在Lee-Carter模型的基础上，通过一个双随机模型对Lee-Carter模型中的时间项进行拟合，很好地解决了Lee-Carter模型在我国的应用问题，结果如下：
1.从预测结果来看，改进后的模型拟合和预测结果比较理想，中国城市人口死亡率存在着明显的下降趋势；
2.漂移项的随机波动对死亡率预测有着显著的影响，这表明样本量少这一不足在利用Lee-Carter模型对我国城市人口死亡率建模时应该引起足够的重视，不应该被忽略；
3.死亡率下降导致的长寿风险对我国企业职工基本养老保险有着重要的影响，不应该被忽视。
参考文献：
[1]Booth, H., J. Maindonald, and L. Smith. Age-Time Interactions in Mortality Projection: Applying Lee-Carter to Australia. Working Papers in Demography, Research School of Social Sciences, the Australian National University, 2002.
[2]Booth, H., Tickle, L. The future aged: New projections of Australia's elderly population. Australasian Journal on Ageing, 2003,22(4),196-202.
[3]Booth, H., Tickle, L. Beyond three score years and ten: Prospects for longevity in Australia. People and Place, 2004,12(1),15-27.
[4]Brouhns, N., M. Denuit, and J.K. Vermunt. A Poisson Leg-Bilinear Regression Approach to the Construction of Projected Lifetables. Insurance: Mathematies and Economics, 2002a,31,373-393.
[5]Brouhns, N., M. Denuit, and J.K. Vermunt. Measuring the Longevity Risk in Mortality Projections. Bulletin of the Swiss Association of Actuaries, 2002b,2,105-130.
[6]Cairns, A.J.G., D. Blake, and K. Dowd. Modeling and Management of Mortality Risk: A Review. Scandinavian Actuarial Journal, 2008a,2-3,79-113.
[7]Carter, L.R. Forecasting U.S. mortality: A comparison of Box-Jenkins ARIMA and structural time series models. The Sociological Quarterly, 1996,37(1),127-144.
[8]Delwarde, A., and M. Denuit. Construction de tables de Mortalité Périodiques et Prospectives, Ed. Economica, Paris, 2006.
[9]De Jong, P., and Tickle, L. Extending Lee-Carter mortality forecasting. Mathematical Population Studies, 2006,13(1),1-18.
[10]Girosi, F., and G. King. A Reassessment of the Lee-Carter Mortality Forecasting Method. Working Paper, Harvard University, 2006.
[11]Girosi, F., and King, G. Understanding the Lee-Carter mortality forecasting method. Technical repert, 2007.
[12]Girosi, F., and G. King. Demographic Forecasting. Princeton University Press, 2008.
[13]Lee, R.D., and L.R. Carter. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association, 1992,87,659-671.
[14]Lee, R.D., and T. Miller. Evaluating the Performance of the Lee-Carter Method for Forecasting Mortality. Demography, 2001,38,537-549.
[15]Li, N., and R. Lee. Coherent Mortality Forecasts for a Group of Populations: An Extension of the Lee-Carter Method. Demography, 2005,42,575-594.
[16]Li, S. H, M. R. Hardy, and K. S. Tan. Uncertainty in Mortality Forecasting: An Extension to the Classical Lee-CarterApproach. Technical Report, University of Waterloo, 2006.
[17]Lindbergsaon, M. Mortality among the elderly in Sweden 1988-1997. Scandinavian Actuarial Journal, 2001,1,79-94.
[18]Pitacco, E. Survival Models in a Dynamic Context: A Survey. Insurance Mathematics and Economics, 2004,35,279-298.
[19]Pitacco, E., M. Denuit, S. Haberman, and A. Olivieri. Modeling Longevity Dynamics for Pension and Annuity Business. Oxford University Press, 2009.
[20]Waegenaere, A. D., B. Melenberg, and R. Stevens. Longevity risk. Working Paper, Tilburg University, 2009.
[21]Wilmoth, J. R. Mortality projections for Japan: A comparisen of four methods. Oxford University Press, New York, 1996.
[22]卢仿先，尹莎.Lee-Carter方法在预测中国人口死亡率中的应用[J].保险职业学院学报，2005,(6).
[23]祝伟，陈秉正.中国城市人口死亡率的预测[J].数理统计与管理，2009,(4).