城镇化的技术创新效应（上）——基于1990-2010年中国区域面板数据的经验研究

    内容提要：城镇化不仅是现代经济生产率的重要推动力，而且是促进技术创新的重要因素。文章在综合已有研究成果的基础上，运用理论分析与实证检验的方法，探讨城镇化对技术创新的作用机理与影响程度。通过对1990-2010年中国总体数据时间序列与区域面板数据的分析发现，无论从全国层面还是七大区域来看，中国城镇化进程与技术创新水平总体上趋于一致；中国城镇化与技术创新、全要素生产率之间呈现高度的正相关；城镇化有助于技术创新，且通过创新效应显著地驱动一国的技术进步即全要素生产率的增长；城镇化的技术创新效应在区域之间存在差异。

关键词：城镇化，技术创新，生产率

        作者简介：仇怡，中国社会科学院城市发展与环境研究所博士后 

        一、引言

城镇化是经济、社会和空间结构的变迁过程，这一过程与技术进步有着密切联系。城镇化的过程即为生产要素的空间集聚过程，而要素的集聚会带来正的技术外溢与扩散效应，从而有利于集聚地的自主创新，最终促进全要素生产率增长。新经济增长理论认为，一个国家经济要实现稳定的可持续发展，资本、劳动力和技术是不可或缺的因素，其中技术尤为重要，而创新则是技术进步的重要原动力。技术创新包括多种因素，如制度变迁、研发投入、人才培养等，随着新增长理论对外部性研究的日益深化，城镇化对技术创新的作用也逐步进入学者的研究范围。目前有关城镇化与技术创新关系的研究，主要集中在3个方面：一是研究城镇化与技术创新的关系。相关文献已基本证实城镇化能给技术进步带来正的外部性，城镇化是一国技术创新不可忽视的因素之一（Chinitz，1961；Pred，1966；Jacobs，1969；Lucas，1988；Feldman等，1999；Carlino等，2007；程开明、李金昌，2008）。二是研究城镇化与经济增长（或全要素生产率）的关系。已有的经验性文献已证实，创新是推动区域经济发展的重要动力，它不仅提高区域全要素生产率，而且有助于产业结构升级，推动区域经济增长方式转变（魏后凯，2011）；Fogarty等（1988）、Moomaw等（1996）、Henderson（2000）、沈坤荣等（2007）、吕健（2011）的研究也发现城镇化是促进经济增长的重要因子。三是综合研究城镇化、技术创新与经济增长（或全要素生产率）三者的关系。程开明（2009）研究认为，城市化通过创新的中介效应推动经济增长；魏下海、王岳龙（2010）研究发现，城市化和创新对全要素生产率增长具有长期的正向影响，城市化通过创新中介效应显著地驱动全要素生产率增长。

由此可见，尽管目前国内外已有一些关于城镇化与技术创新、全要素生产率（或经济增长）之间关系的研究，但详细考察城镇化对技术创新促进作用的文献偏少。已有文献大多是把城镇化的技术创新效应作为其促进经济增长的中介效应来研究，缺乏对城镇化促进技术创新机理的探讨。基于此，本文将在探讨城镇化促进技术创新作用机理的基础上，采用相关时间序列与区域面板数据对中国城镇化的技术创新效应进行经验研究。

二、城镇化的技术创新效应作用机理与模型设定

发达国家的经验表明，城镇化与技术创新之间可以形成良性循环。技术创新是当前各国经济发展和社会进步的重要动力，在现代经济体系中，技术创新与知识溢出最容易在空间上相对集中的个体之间发生，因而城镇化为这种创新与外溢提供了契机。城镇化是人类生产和生活活动在区域空间上的聚集，也是创新和技术进步的主要来源，是推动全要素生产率增长的重要引擎。可以说，城镇为技术创新及扩散提供了良好条件，城镇化通过技术创新实现全要素生产率的增长，进而推动整个区域的经济增长。本文认为，城镇化的技术创新效应主要是指城镇化过程中，由于人口迁移、要素集聚、空间扩散等各种诱因引发的技术变革与创新，因此城镇化不仅是现代经济生产率的重要推动力，而且是促进技术创新的重要因素。城镇化对技术创新的作用主要基于两个方面：一是随着人口向城市的迁移，经济活动也向城市地区聚集，从而引致更多的技术创新活动，理论上说城镇化程度越高，城市规模越大，技术创新活动越多；二是城市化的过程会带来创新产品和知识技术的外溢与扩散，这又会进一步促进当地的技术创新，形成“创新一外溢（扩散）一再创新”的良性循环。

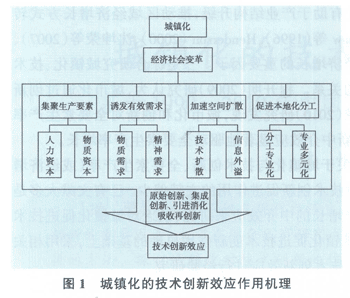
城镇化和技术创新过程与人力资本、物质资本等其他要素密切相关，理论上说，城镇化能够产生正向的技术创新效应，即随着城镇化的不断推进，全社会的人力资本水平会不断提高，生产要素会不断集聚，有效需求会不断增加，知识外溢会不断加速，最终促进技术创新活动的形成与发展（见图1）。

 

        为了考察城镇化（URB）通过技术创新影响全要素生产率（TFP）的程度，本文用城镇化与技术创新（研发经费投入RD、专利授权量PG）的交互项来分析城镇化的技术创新效应，由此建立模型：

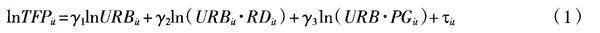
式中，如果交互项的系数为正，则说明城镇化能带来技术创新效应，并能最终促进全要素生产率增长；反之若系数为负（或不显著），则表明城镇化不能产生技术创新效应。

三、中国城镇化进程与技术创新水平的演变轨迹与关系描述

（一）基于国家层面的中国城镇化进程与技术创新水平的关系

伴随着国民经济的快速增长，中国的城镇化进程加速推进，城市规模不断扩大，城镇化水平稳步提高。2010年中国城镇人口达66978万人，城镇化率为49.95%。与此同时，中国的技术创新活动也有显著发展，这里从技术创新活动的投入和产出两个角度，分别选取研发经费支出占当年GDP的比重、发明专利授权量占当年总授权量的比重作为衡量指标。1990-2010年，中国的研发支出总量与专利授权量呈逐年递增之势，特别是2000年以来，中国研发经费支出以年均23%的速度快速增长，2010年中国研发经费支出达7062.58亿元，占全年GDP的1.76%，创历史新高，并首次超过德国，位居世界第三位（仅次于美国和日本）。不过，1990-2010年，在中国授权的3种专利中，发明专利的授权量过少是最突出的特点。由于反映技术创新水平的相关指标只能获取1990年以来的数据，因此，这里只分析1990-2010年中国城镇化进程与技术创新水平的关系与变化趋势（见图2）。通过比较全国城镇人口和研发投入的增长速度，可以发现，20年来全国城镇人口的平均增长速度为3.98%，而全国研发经费投入的平均增长速度为21.93%，研发投入的增长率明显快于城镇人口的增长率。

 

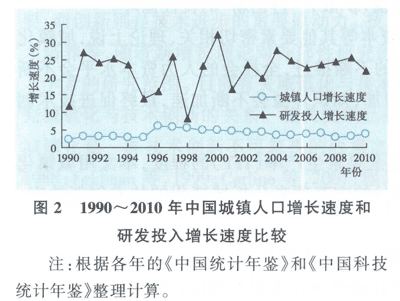
另外，以发明专利授权量占总授权量比重表示的技术创新活动产出水平的变化趋势呈现出一定的阶段性特征，大致可以分为3个阶段：（1）1990-1997年，中国发明专利授权量的比重从16.99%下降到6.85%；同期城镇化率由26.41%增至31.91%。（2）1998-2004年，这一比重从6.97%上升到25.9%；同期城镇化率由33.35%增至41.76%。（3）2005-2010年，这一比重又从24.9%变化到16.58%；同期城镇化率42.99%增至49.95%。可见，中国技术创新产出的阶段性变化与城镇化率一直逐年递增的演变趋势不一致（见表1）。

 

        （二）基于区域层面的中国城镇化进程与技术创新水平的关系

改革开放以来，在国家政策的大力支持下，中国东部沿海地区经济取得了长足发展。尽管近年来国家投资布局和政策支持的重点开始逐步移向中西部和东北地区，但地区差异仍然明显，这不仅表现在经济增长的速度上，同样也表现在城镇化水平上。考虑到东部和西部地区的内部差异性，根据魏后凯等（2010）的思路，本文按照七大区域的地域框架进行分析，即东北（辽宁、吉林、黑龙江）、东南（广东、福建、海南）、长三角（上海、浙江、江苏）、环渤海（北京、天津、河北、山东）、中部（山西、安徽、江西、河南、湖北、湖南）、西南（广西、重庆、四川、贵州、云南、西藏）、西北（内蒙古、山西、甘肃、宁夏、青海、新疆）。通过整理七大区域城镇化与技术创新投入产出的相关数据可以发现，中国不同区域的城镇化进程与技术创新投入产出紧密相关，城镇化进程较快的地区其技术创新水平也比较高，城镇化与技术创新呈正相关。如长三角、环渤海、东南这三大区域的城镇化率分别位居全国第一、第二和第四位，而其研发经费、专利授权量也均列全国前三，且各区域的城镇化率与技术创新状况排名趋势也基本一致。

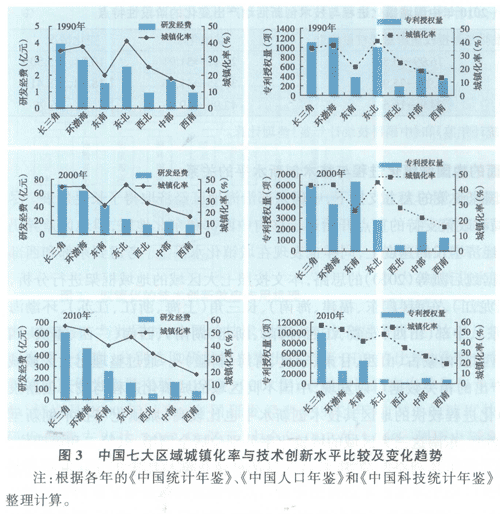
图3描绘了七大区域的城镇化进程与技术创新演变趋势，可以看到，中国各区域的城镇化进程与技术创新水平变化趋势基本一致，城镇化水平随着技术创新投入的增加而提高，城镇化水平的提高反过来又促进了技术创新产出，二者之间呈现高度的正相关。首先，从技术创新投入来看（主要是研发资金和研发人员的投入），技术创新集中于大城市，而且城市规模越大，创新投入规模也越大，城市化对技术创新具有促进作用。从图3可以看出，长三角及环渤海地区是中国经济最发达地区，城市规模逐年增大，而创新投入也是七大区域中投入最多的地区。另外，从空间梯度来看，技术创新往往发生在大城市，西南地区是七大区域中城镇化水平最低，创新投入也最低的区域，而西南区域的城市规模也是中等水平。这说明，中国城镇化水平越高的区域，其资金与人员投入越大，空间聚集效应越强，则越有利于技术扩散，其技术创新能力就越强。其次，技术创新产出不仅受创新投入、城镇化水平和城市规模的影响，同时不同区域的经济发展水平、地理位置、资源禀赋差异、产业基础、市场结构、政策环境和区域开放程度也会影响区域的创新产出。长三角、环渤海及东南地区开放程度较高，其创新投入、创新产出和城镇化水平居全国前列，开放程度会影响区域的技术扩散能力，开放程度越高，区域的技术扩散能力越强。第三，中国区域城镇化水平地区差别较大，2010年城镇化率最高的长三角地区与最低的西南地区相差39个百分点。可见，中国区域之间城镇化水平的不均匀，一定程度上带来了区域之间创新投入与产出的差别，而创新投入与产出的差别又进一步加大了城镇化水平的地区差异。

  

        四、城镇化的技术创新效应：基于中国的实证检验

（一）中国全要素生产率的估算

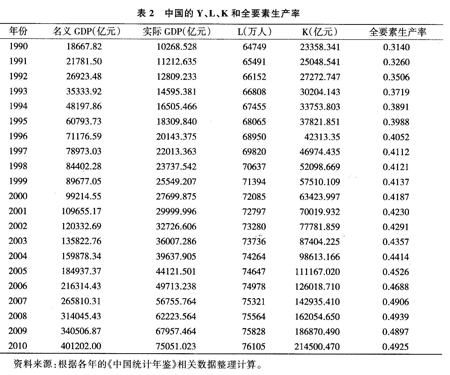
本文关于全要素生产率的计算采用传统的Cobb-Douglas生产函数Y_t=A_tK^α_tL^β_t进行估算。其中，总产出水平（Y）用国内生产总值（GDP）来反映，并且使用GDP平减指数将其换算成以1978年为基期的实际GDP；资本（K）以各年度的资本存量表示，这里按照张军等（2003）的资本存量测量方法进行估算；劳动力（L）以全社会就业人数表示。其中，L的数据可以直接从中国历年统计年鉴中获得，总产出水平依据2011年《中国统计年鉴》中的历年GDP指数折算为以1978年为基期的实际GDP。

关于资本存量K的测算，本文采用Coldsmith于1951年开创的永续盘存法，通过公式：K_t=I_t/P_t+（1-δ_t）K_t-1计算出1990-2010年各年的实际资本存量。公式中K_t为t时期固定资本存量，I_t为t时期固定资本形成总额，P_t为t时期固定资产投资价格指数，δ_t表示t时期的折旧率，K_t-1表示上一期固定资本存量；本文以1978年为基期，计算出1990-2010年的固定资本存量。最后，使用Y、K、L的时序数据进行回归可以估计出平均资本产出份额和平均劳动力产出份额，然后根据索洛残值法计算出各年份的全要素生产率TFP，具体结果如表2所示。