高维模型选择方法综述（三）

2Dantzig Selector方法
    针对变量数大于样本量的高维模型选择问题，Candes和Tao[28]提出了Dantzig Selector（DS）方法。DS方法的参数估计为下述凸优化问题的解：
    
    
    
    正如上面所说，在“一致不确定原则”下，DS方法参数估计的误差有很好的控制；LASSO方法参数估计的相合性需要“不可表示条件”的支撑。特别地，Meinshausen和Yu[30]推导了在一个对设计阵要求比“一致不确定原则”更宽松的条件下，LASSO方法参数估计的均方误差以一个更小的概率限制在与上述DS方法相同的范围内。文献中没有一个确切的结论说明DS与LASSO哪种方法更优。另一方面，二者形式的相近性自然引起人们探索二者联系的兴趣。事实上，Meinshausen等[29]给出了二者结果相同的充分条件。在p≤n的前提下，记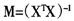，若满足对角线主导条件：
    
    LASSO方法与DS方法的结果完全相同。特别地，当p=2时上述条件总成立，即二者总相同。
    3基于变量降维的模型选择方法
    3.1主成分回归
    主成分分析（PCA）是对原始变量进行线性变换，得到一组线性无关的潜变量。得到的变量是按照解释原数据方差大小排序的。换言之，可将主成分分析看做是对坐标系的旋转，使得数据在第一维坐标方向上方差最大，在第二维坐标方向上次之，依次类推。特别地，主成分得分可由设计阵衍生矩阵的特征向量求得，相应的特征值大小表征了解释方差的大小。主成分分析的内容可在一般多元统计教科书中找到详细描述。
    主成分回归（PCR）是将主成分分析和回归分析相结合的方法，是探索性数据分析常用的方法之一[31]。根据线性回归的线性不变性，若采用全部主成分拟合回归，则得到与原始变量相同的拟合结果。实际应用中，可根据需要选取前几个主成分建立模型。PCR的一大优势在于其自变量是线性无关的，避免了线性回归中共线性性的问题。原变量中具有共线性性的变量通过线性变换结合在一起，使得拟合的模型更容易解释。因此，当自变量有较强的共线性性时，适宜考虑采用PCR建立模型。除此之外，PCR通过选取少量的潜变量拟合模型，有效避免了过度拟合的问题，因而一般来说具有更高的预测准确性。Naes和Martens[32]指出PCR具有很好的应用价值。
    PCR中主成分个数的选取与主成分分析有所不同。主成分分析是以尽可能多地提取变量信息为目的，而PCR则是以回归为目的。因此前者多依照主成分解释方差的比例选取变量数目而后者则多根据舍一验证等方法选取主成分数目。PCR中主成分个数可以看做调整参数，在第四节中我们将介绍更多调整参数的选取方法。
    3.2偏最小二乘
    偏最小二乘（PLS）方法最早出现于Wold[33]。PLS方法已被广泛应用于候选变量较多的模型选择问）题，相应综述可参考Tobias[34]。
    
    上述表达式与主成分分析的求解公式类似。事实上，PLS方法与PCR方法有很多相似之处。二者都是采用选取少量潜变量代替原始变量，从而达到降维的目的。选取潜变量的数目可以看做是调整参数。随着潜变量数目增加，数据拟合度相应增加，但并不意味着预测精度也相应增加。特别地，当潜变量数目与原变量数目相同时，选择模型与全模型完全相同。值得注意的是，PLS的潜变量作为原始变量的线性组合，其权重不是响应变量和自变量的线性函数，因而增加了计算的难度。通常需要借助数值计算方法得到权重，具体算法可参考Hoskuldsson[35]及Jong[36]。
    PLS和PCR的差别在于前者选取潜变量是以与响应变量的相关性为导向的，而PCA方法则不需要响应变量的信息，只是选取方差最大的线性组合。从这个角度可以看出，当降维目的在于提高模型预测的准确性时，选用PLS方法更为明智，而PCA方法则侧重提取自变量的信息。Stone和Brooks[37]将PLS、PCR以及OLS（普通最小二乘）三种方法统一到同一个理论框架下，并指出OLS方法和PCR方法是连续谱的两个极端情形，而PLS介于二者之间。类似于Bridge方法，在该理论框架下，还可以讨论连续谱对应的其他可能的方法。文中通过多个实际数据例子比较了不同方法的参数估计准确度和预测精度。有兴趣的读者可以参考Stone和Brooks[37]。
    Datta等[38]比较了PLS方法和LASSO方法在高维数据中的应用。他们指出两种方法均适用于变量维数较高的情形，但当变量中有较多噪音时，LASSO方法的预测精度较PLS更高。Nguyen和Rocke[39]，Nguyen[40]则将PLSS方法应用于微阵列数据分析，并对二分数据和删失数据做了相应调整。
    3.3充分降维
    
    
    4调整参数的选取
    在模型选择的方法中，调整参数的选择起着十分重要的作用。在前面很多地方已经提到了调整参数，例如惩罚最小二乘中连接最小二乘项与惩罚项的参数等，它用于在模型拟合优度和选择模型的复杂度之间取得平衡。由此可见，调整参数对于最终选择怎样的模型有着决定性作用。不同的调整参数选取方法往往侧重点不同，有的倾向于选择模型预测的准确性，有的倾向于相合性。本节着重介绍交叉验证方法及各种推广方法，还会涉及误选率、稳定路径等选择方法。
    4.1交叉验证
    
    最小化上述公式得到λ的方法即为交叉验证。
    记A（λ）为n×n的影响矩阵，满足
    
    4.2广义交叉验证
    广义交叉验证由交叉验证方法推广而得。在交叉验证的调整参数估计式中，将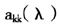用对角线元素的平均值代替，得到新的交叉函数如下：
    
    使上述函数达到最小的λ即为广义交叉验证法选取的调整参数。
    广义交叉验证的理论性质在Li[47]中有详细讨论。利用随机求迹方法计算trA（λ）的问题可以参考Hutchinson[48]，另一种不同的计算方法参见Golub和VonMatt[49]。
    4.3广义近似交叉验证
    
    广义近似交叉验证的目标是将真实概率分布和估计分布的相对KL距离最小化。相对KL距离CKL（λ）定义为
    
    其中A（λ）为影响矩阵，W是对角矩阵，对角线的元素为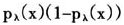，即伯努利分布的方差估计。
    广义近似交叉验证的一个修改版本是B类广义近似交叉验证。前者的目标在于最小化CKL（λ）而后者的目标为选择真实的变量。B类指的是对模型的稀疏性有先验的信息，类似于BIC准则中的B。就像AIC是侧重于模型预报的选择准则，BIC是侧重于模型相合性的选择准则，广义近似交叉验证和B类广义近似交叉验证分别对应于AIC准则和BIC准则。在AIC到BIC的转换中，假定γ是模型的自由度，则BIC将γ替换为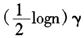。类似地，我们可以如下由广义近似交叉验证得到B类广义近似交叉验证。令γ表示伯努利惩罚模型中代替自由度的量
    

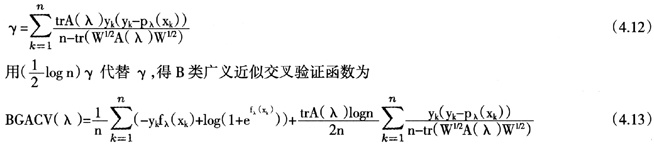
（未完待续）