基于元回归分析的外商直接投资对中国生产率溢出效应的实证研究(二)

(二)元回归分析模型
    
    传统文献综述的局限是只能进行定性描述和总结，而元回归分析则通过计量经济学方法具有了以下新的功能：一是解决各研究结果之间的分歧，通过异质性检查揭示研究变量间的真实关系，提高统计分析的功效。二是扩大了样本容量，解决了小样本研究所存在的一些问题。元回归分析提供了某一个相关主题在一段时期内比较系统、全面的研究整合，克服了单项研究中存在的一些局限，如个体研究者的学科局限、信息不完全等。同时，还在一定程度上回避了原始文献中存在的选择性偏误和模型设定偏误等问题。三是对新的研究问题起到了启发作用。四是代替大规模的调查研究，可以节约大量的研究费用及时间，从而提高研究的层次与水平。
    为解释样本论文关于FDI溢出结果的差异，本研究采用了Stanley和Jarrell(1989)的Meta回归分析计量模型：
    

    其中，Meta回归分析的被解释变量Yj一般为相关参数估计量的t值，t值来源于实证论文中的N份结论，N为Meta回归分析的样本容量。Meta回归分析的K个解释变量Zjk(k=1，2，…，K)是反映所有实证研究设计特征的代理变量，用以描述各项研究在样本数据选择、模型设计、估计方法等方面的差异。
    如前所述，由于各实证研究的数据不同，有的解释变量采用FDI水平值(如蒋殿春等，2008)，而有的则采用比值——FDI/资本(如沈坤荣，2001)。由于不同的解释变量对FDI溢出的估计参数大小影响十分不同，而采用估计参数的t值则能进行横向比较，因此为Stanley和Jarrell(1989)所推荐。
    (三)变量说明
    
    根据(1)式所构建的模型，需要进行有关解释变量的选择，进而分析样本论文的异质性。本文的Meta 回归分析的被解释变量为FDI溢出效应参数估计量的t值，而如何选择元回归分析中的解释变量，目前还没有可支持的经济理论作指导。为此，本研究在借鉴国内外已有研究的基础上，根据样本论文所提供的参数特征进行解释变量的选择，将解释变量划分为五类(如表2所示)。第一类为生产率溢出测度变量，包含产出(GDP)与生产率两个变量。在所选择的31篇论文(75个样本)中，回归方程多用产出(GDP)作为被解释变量(占65%)，其他则采用全要素生产率(TFP)或技术生产率TP(合计占35%)等作为被解释变量，笔者将后者统一为生产率变量。第二类为FDI代理变量。不同论文的FDI代理变量差异较大，有的选择了外资资产值或比重(如何洁，2000)，有的则选择雇员人数或比重(如Tian，2004)，这对溢出结果将产生不同的影响。第三类为数据特征变量。由于样本采集多为20世纪90年代后，大多数样本采用的是面板数据，占到样本的85%；另外，由于多数论文数据采集自《中国统计年鉴》，国内以省际数据(41%)为主来构造面板数据，而国外论文则以企业数据为主，这是国内外有关FDI溢出研究主要不同的方面之一。第四类为特定解释变量。Javorcik(2004)的实证研究结论为垂直溢出比水平溢出更显著，而Caves(1974)的结论是水平溢出为正且显著，为此将这一争论作为哑元变量纳入本模型中；在样本论文中将研发(R&D)、人力资源质量(LQ)以及技术差距(GAP)作为溢出影响因素的分别占到了25%、33%和20%，因此有必要纳入到哑元变量中考察。第五类为其他变量，主要包括了样本观察数的对数平方根、研究的平均年、论文语言以及行业等。Görg和Strobl(2001)认为样本观察数的对数平方根是一个重要的影响因素，例如本研究的样本数由28(辛永容等，2009)到188(Sun，2011)不等，而样本数的大小是t值的函数，其影响显而易见。由于不同论文发表年份及研究时间跨度不同，也将会影响t值，在本研究中将考虑研究年的因素。我们初步判断国内外在研究方法上存在一定的差异，可能会对溢出结果产生影响，因而将其选为哑元变量。
    

三、Meta回归分析结果讨论
    
    元回归分析采用了Stata11.0，运行结果如表3所示，回归采用的是普通最小二乘法(0LS)。正如Stanley 和Jarrell(1989)所指出，由于样本来自不同的数据，采用截然不同的研究方法，元回归分析的误差项可能存在异方差。表3中的模型(1)-(4)采用普通最小二乘法(OLS)，包含异常值(全部75个观察值)，而模型(5)-(8)则采用了稳健标准误回归(Robust SE)，剔除了1个异常值(赖明勇，2005)。考虑到多重共线性问题，对变量进行了简单相关分析，部分变量间存在相关性，如y_output和y_productivity、GAP间存在相关性，尽管呈相关性(0.05水平)，但大多相关系数均较小，为排除多重线性的影响，在模型设定中剔除了相关变量影响(如模型(2)和模型(6))。为考察多变量综合作用，仍采用了两个全模型(4)与模型(8)。
    

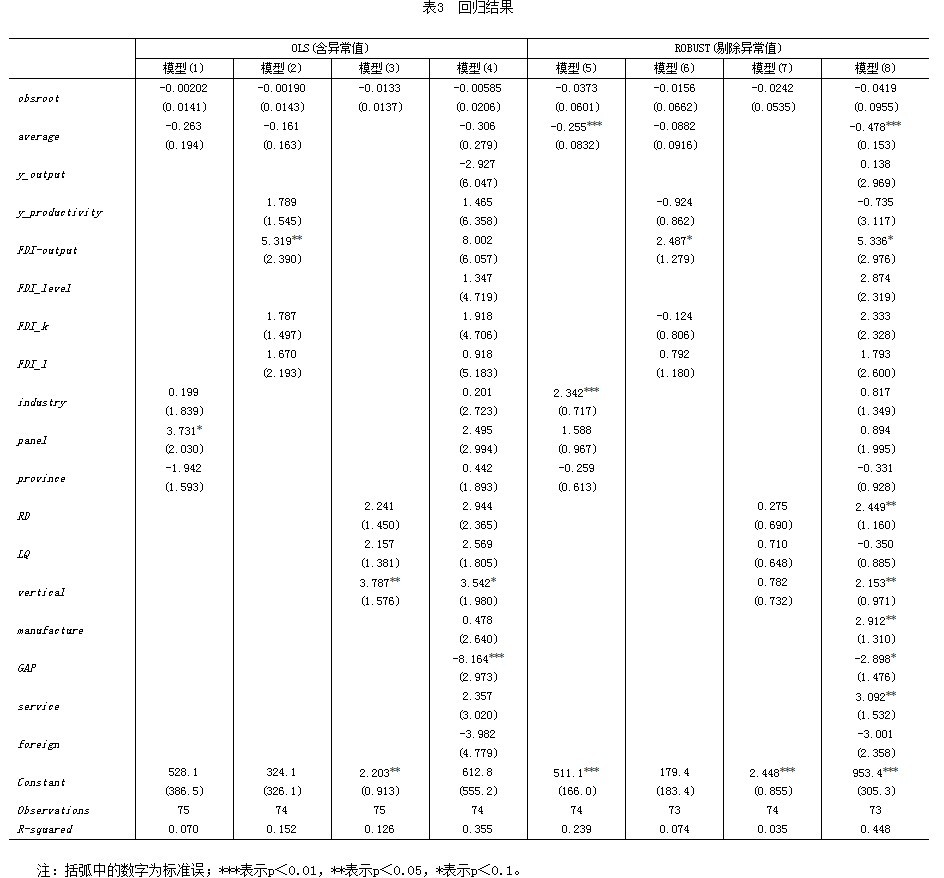
Görg和Strobl(2001)认为FDI代理变量不同对研究结果有重要影响，其结论是采用产出水平值(或比例)的FDI代理变量较其他形式代理变量(如资本或雇员)有较低的溢出效应。本研究的结论与Görg和Strobl(2001)相反，FDI代理变量为产出值的样本表现出溢出统计显著，而大多样本采用的是FDI水平值，溢出效应不显著。这表明，如何恰当地定义FDI溢出变量是正确测度FDI溢出的关键。早期的研究主要集中在水平溢出(如Aitken，1999；陈涛涛、陈娇，2006)，而Javorcik(2004)指出，由于跨国公司有阻止泄露先进技术给东道国行业内竞争者的激励，导致行业内溢出效应不显著或为负。本研究结论表明垂直溢出效应显著，即垂直溢出(前向与后向溢出)高于水平溢出，从而解释了挤出效应。FDI的资本与劳动代理变量的溢出效应不显著。
    从数据特性变量分析，模型(4)和模型(8)表明，R&D、垂直关联(vertical)对溢出有显著影响，并呈现正效应。由此可见，研究设计的不同会对FDI溢出效应的t值产生显著的影响。关于数据特征的影响，模型(1)采用面板数据的样本的t值较高，表现出较高的溢出效应，而模型(5)则表现为采用行业数据有明显的正溢出(显著水平达0.01)。样本数量的影响似乎与我们预期不符，即8个模型均未通过显著性检验，表明样本数的大小对溢出影响不大，这与Görg和Strobl(2001)的研究结论一致。技术差距(GAP)变量在两个模型(5)和(8)中均呈现负值，且通过显著性检验，说明技术差距过大并不利于FDI的吸收与消化。
    从研究时间的跨度看，数据的平均值均为负值，模型(5)和(8)均通过显著性检验，表明早期的FDI溢出效应更为显著。时间跨度的均值为2000.05，这意味着2000年后的FDI溢出效应呈下降趋势，这与Wooster (2010)的结论相反，这可能是因为本研究仅涉及中国的数据，未考虑各国间吸引FDI的竞争因素。目前国内外有关FDI效应的研究大多集中在制造业，对服务业的研究相对较少，而服务业通过显著性检验(0.05水平)，表明服务业FDI有显著的正溢出效应。从表3还可以看出，发表在国外与国内论文的溢出效应不存在差异性，与笔者研究设计之初的预测相反，其原因可能是所采用的数据均来自国内的统计年鉴，运用的方法没有大的差异。
    总之，关于中国FDI溢出的研究结果差异，除上述数据类型、代理变量、时间等因素外，还有可能是部分研究存在一定的模型设定错误。
    四、结束语
    自改革开放以来，随着国家投资政策及环境不断改善，我国吸引外资由1979-1984年的41亿美元上升到2009年的900亿美元，增长约22倍，吸引外资总额仅位居美国之后，居世界第二位。在改革开放三十多年的经济飞跃发展中，FDI无疑是起到了重要的作用。正如Ljungwall(2008)研究结论一样，中国相对于其他发展中国家或转型国家有着更高的FDI溢出效应。
    （作者： 武汉理工大学管理学院 徐宏毅 蔡萌 武汉理工大学图书馆 赵迎红）