中国社会的代际收入流动性趋势：2000～2009(二)

        一般来说，为了估计代际收入弹性的时间变化趋势，大都使用同一年或者临近几年出生子代作为某年代际收入弹性估计的子辈群体。在此，我们考虑每年中25～34岁的子辈作为一代。如表1所示，经过上述处理，2000年有133个配对家庭，2004年有114对，2006年有92对，2009年有104对。在2000年中子辈样本的平均年龄是28岁，出生的年份是1966年到1975，恰好是文革十年出生的人群。这一人群的工作很大程度上受到了计划体制的影响。随后接下来的是1970年后人群，这里面有大部分人是顶替父母工作而就业，即“接班”，还有相当部分是自由就业，因为这一人群最年轻的一代是1979年出生的。如果他们20岁就业，即1999年，正好赶上了大学生不包分配的年代。2006年的25～34岁人群是在1972年至1981年出生的，2009年25～34岁人口是在1975～1984年出生的。为了避免2009年中与2000年的有同一年出生的情况，我们考虑了2009年处于24～33岁人群。这样不同时间的子辈平均年龄是28、28、29、30和30岁，接近他们人生中达到平均收入的年龄段。
    表1  子辈和父辈年龄的均值描述

子辈样本年份		2000年25～34岁	2004年25～34岁	2006年25～34岁	2009年25～34岁	2009年24～33
子辈出生年份		1966～1975	1970～1979	1972～1981	1975～1984	1976～1985
子辈平均年龄		28	28	29	30	30
父辈平均年龄	1989	44	41	40	39	38
	1991	46	43	42	41	40
	1993	48	45	44	43	42
样本量		133	114	92	104	98

    在父辈平均年龄的描述统计中，1989年这一行对应的平均年龄分别是2000年子辈年龄在25～34岁的父亲在1989年时的平均年龄，其他各年解释相同。我们可以看到2000年的子辈对应的父辈在1989年时的平均年龄是44岁，1991年是46岁，1993年是48岁。由于每一个待估年份配对的子样本中样本量相同，因此父辈的平均年龄1991年比1989年大两岁，1993年比1991年大两岁。因此父辈年龄的两年或者三年的平均很容易算出来，就是对应年份平均年龄的再平均。因此，我们也只要知道1989年的平均年龄就可以推断各年以及几年平均的年龄。2004年子辈的父亲在1989年的平均年龄是41岁，2006年的是40岁，2009年的是39岁。父辈在1989、1991和1993年内三次调研的平均年龄正好就是1991年的平均年龄，分别是46、43、42、41岁。因此，三年来看，2006年和2009年样本父辈和子辈的收入都更接近他们各自的一生平均收入。由于2000年跟1989年间隔时间太近，因此可以看到2000年配对的父子中，子辈的平均年龄偏小，父辈的平均年龄偏大。这会导致2000年估计向下偏误最大。其他各年的子辈和父辈年龄差异很小，因而2004、2006和2009年之间估计因收入在不同年龄段度量导致的低估差异较小。
    由于同住家庭样本有高估社会总体的代际收入弹性趋势，考虑到中国父母与成年子女居住的比例随时间越来越小，因而CHNS样本会随着时间往后推移高估越大。基于对年龄的控制可知，各年的代际收入弹性估计中因年龄的差异导致的估计偏误变小且方向明了，而各年因子代与父代同住导致高估的时间趋势也很明了，因而有利于我们判断真实的代际收入弹性趋势。关于各年度子代和父代的收入描述统计见附录表1-4。
    四、代际收入流动性的估计与解释
    根据上一节估计方法的讨论，我们把式(5)代入式(1)得到如下估计方程：
    y_its=β_ty_icf-a_tsage_its-b_tsage_its²+β_ta_cfage_icf+β_tb_cfage_icf²+ε_its^*    (6)
    其中i表示第i个家庭，t表示子辈样本所在年份，即四个年份2000、2004、2006、2009，s表示儿子，f表示父亲，c表示父亲的年龄或者收入度量年份，age_its和age_icf分别表示i家庭子辈在t年的年龄和父辈在c年的年龄，ε_its^*=ε_its-v_its+β_tv_icf。
    首先，我们在上一节描述的样本内，只考虑父亲一年的实际收入作为解释变量，随后我们考虑父亲收入的两年平均以及年龄的两年平均，然后是父亲变量的三年平均作为解释变量，分别估计出2000、2004、2006和2009年四个年份的代际收入弹性。
    表2是我们对中国代际流动性的时间趋势估计。简化起见，我们没有给出其他系数，只列出了代际弹性系数及其相应的估计标准误。第2～4行，是对每个t，c分别取1989、1991和1993时的代际弹性。我们可以看到，即使控制了年龄的趋势，使用单个年份的父辈数据，而且是严格控制父亲年龄范围使其尽可能地保持在接近其一生平均收入的年龄附近，也还是会有很大的偏误。如2006年的弹性估计，使用1989年的父辈收入，出现了较大的负值估计系数(-0.15)，使用1991和1993的父辈收入却得出了相对较大的正弹性系数(0.39和0.45)。这可能与单个年份的收入数据受经济暂时波动，特别是一些未预料到的大的经济冲击影响，以及收入数据的报告误差有关。
    表2  代际收入弹性的趋势估计

	(1)     2000年25～34岁	(2)     2004年25～34岁	(3)     2006年25～34岁	(4)     2009年25～34岁	(5)     2009年24～33
1989	0.40     (0.10)	0.16     (0.11)	-0.15     (0.14)	0.12     (0.12)	0.10     (0.12)
1991	0.52     (0.10)	0.24     (0.14)	0.39     (0.15)	0.33     (0.15)	0.30     (0.15)
1993	0.47     (0.10)	0.36     (0.11)	0.45     (0.10)	0.33     (0.12)	0.35     (0.12)
1989～1991两年平均	0.66	0.34	0.14	0.33	0.30
	(0.12)	(0.16)	(0.18)	(0.17)	(0.17)
1991～1993两年平均	0.69	0.48	0.62	0.49	0.49
	(0.12)	(0.14)	(0.14)	(0.16)	(0.16)
1989～1993三年平均	0.80	0.54	0.46	0.46	0.46
	(0.13)	(0.16)	(0.17)	(0.17)	(0.18)
年龄趋势相同	0.77     (0.13)	0.54     (0.15)	0.48     (0.18)	0.45     (0.17)
四个系数是否相等	F值=0.98,P值=0.40

    注：括号内的数为系数的标准误。
    第5行是以1989和1991两年平均的父辈收入作为父亲的一生平均收入代理变量的估计。此时，我们发现2006年的代际弹性数值变为正了(0.14)。除了2006年的系数估计值没有表现出单调递增的趋势外，其他年代的代际弹性估计在1989和1991两年平均的基础上大于单年估计值。这在一定程度上说明了，在控制住年龄趋势的影响后，两年平均能够消除一年数据的波动误差。第6行的1991和1993年的平均的系数估计要远高于使用1989和1991年平均的估计。这说明使用的1989年数据有较大的偏误。
    使用1989、1991和1993三年的父亲收入平均作为父亲的持久收入度量，发现2006和2009年系数处于上述两个系数的中间，而2000年和2004年却比两年平均估计要大，没有表现出在标准的误差模式中越多年平均估计越大的结果。显然更多年份的平均，使得使用父辈单年收入估计的较大波动得到了平滑。由于2009年子辈中最老的一群人与2000年子辈中最年轻的人出生于同一年，为了说明十年之后是完全不同的一代人，我们也估计了把2009年中最老的一代去掉，同时把最年轻的推后一代，这样正好也是十年的组群。表2最后一列就是上述处理后估计的结果。我们发现该估计的系数值与使用1975年至1984年出生群组的估计，无论是单年还是多年的父辈变量平均估计，几乎没有差异。这也说明2009年估计的代际流动性是很稳健的。
    三年平均估计得到2000、2004、2006和2009年的代际收入弹性为0.80、0.54、0.46和0.46，其趋势是从2000年以来，中国社会的收入流动性在不断地改善。
    同时，我们合并四年的回归，并使得每年中子辈的收入年龄趋势一样，父辈的年龄趋势也相同，只不过是各年的配对组有自己的截距。即我们估计如下方程：
    y_its=α_t+β_ty_icf-a_sage_its-b_sage_its²+a_fage_icf+b_fage_icf²+ε_its^*    (7)
    (7)式合并方程得到的2000年后四年的代际收入弹性分别是0.77、0.54、0.48、0.46，与方程(6)分别估计的结果没有太大的差别。我们用这一方程来检验4个代际弹性系数是否相等的F检验，发现并不能拒绝它们相等的原假设。虽然我们严格地控制了年龄范围以及年龄趋势，但还是存在估计偏误，需要对估计偏误进行严格的讨论才能确定真实的趋势。
    从表2的结果可知，父辈单年收入的使用使得估计的波动很大。我们通过考察附表1～4的收入描述统计可知，或者是出于误差或是由于研究者或是调查员不可观测的冲击导致，其中的一些收入是异常的。不管是子辈还是父辈，很难想象年收入只有44，因而收入可能存在异常值的影响。为了剔除这些异常值的影响，我们把父辈的实际年收入低于120元的家庭去除。同时，我们认为2000年和2004年子辈的实际年收入至少不低于600元，2006年的实际年收入不低于1000，2009年的实际年收入不低于1200。经过上述处理之后，我们得到了2000、2004、2006及2009年的配对家庭数分别为121、108、86和98。表3是去掉异常收入值后与表2对应的(1)-(4)列代际收入弹性的估计。
    在表3中可以看到，去掉异常值后，以1989年父辈的实际收入作为其持久收入代理变量的估计，与1991年和1993年的差异变小了，而2006年代际收入弹性由原来的较大负数变为了接近于0的数。同样，1989和1991年的两年平均与1991年和1993年的两年平均之间差异也变小。上述的这些变化在一定程度上又降低了3年平均估计误差。以父辈变量的3年平均样本为例，去掉异常值后2000、2004、2006和2009年的代际收入弹性估计为0.66、0.49、0.35、0.46。除了2000和2006年的估计收到较大影响外，其他系数的估计变化不大，但是总体的趋势还是较2000年以来有所下降。我们也给出了该样本下的估计方程(7)的回归结果，其表现的2000年以来的代际收入弹性估计与分开回归的结果没有太大差异。四个系数是否相等检验的F值为0.65，没有拒绝它们相等的原假设。
    表3  去掉收入异常后的估计

	(1)     2000年25～34岁	(2)     2004年25～34岁	(3)     2006年25～34岁	(4)     2009年25～34岁
样本量	121	108	86	97
1989	0.35	0.11	-0.06	0.22
	(0.11)	(0.09)	(0.11)	(0.10)
1991	0.32	0.19	0.30	0.25
	(0.11)	(0.12)	(0.12)	(0.15)
1993	0.38	0.41	0.36	0.30
	(0.10)	(0.09)	(0.09)	(0.10)
1989～1991两年平均	0.53	0.25	0.14	0.34
	(0.13)	(0.14)	(0.14)	(0.14)
1991～1993两年平均	0.51	0.47	0.47	0.43
	(0.11)	(0.12)	(0.12)	(0.14)
1989～1993三年平均	0.66	0.49	0.35	0.46
	(0.13)	(0.14)	(0.14)	(0.14)
年龄趋势相同	0.61	0.46	0.35	0.47
	(0.12)	(0.13)	(0.15)	(0.15)
四个系数是否相等	F值=0.65，P值=0.58

    注：括号内的数为系数的标准误。
    Becker和Tomes(1986)以及Solon(2004)在一个利他主义框架下，建立了父母基于自己的消费和小孩投资考虑最大化自身效用模型，从理论上推断了父母的基因和家庭文化的影响即继承系数会提高代际收入弹性。继承系数又与子女与父母待的时间成正比。因此，我们如果使用父母与子女居住在一起的样本估计，则会高估整个社会的收入代际弹性，且整个社会中成年子女与父母同住一起的比例越低，则导致高估越严重。我们从2000年，2005年1%的抽样和2010年的人口普查数据，可以基本判断出成年子女与父母居住的趋势。图2是三代以上同堂居住的比例。该图说明从2000年以来，中国社会的核心家庭越来越多，父母与成年子女居住一起的比例越来越低。
    
    
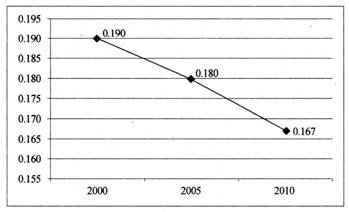
    图2  三代以及三代以上同堂的家户比例
    因此，即使我们的回归结果得出并没有估计系数真值不同的检验，但是考虑到这里CHNS样本的特征，即只有父母与成年子女居住在一个家庭才能够观测到收入数据。这一因素会导致越是早期的数据，高估社会收入代际弹性的部分越小，而越是后期的数据高估越大。由于我们严格地控制了子辈和父辈年龄的范围，使得每年的代际收入弹性估计因年龄导致的偏误变小。因此，考虑父代和子代同住导致高估的因素，即使是各年的样本估计值相等，我们仍然有理由判定2009年整个社会的实际弹性系数低于2000年。在考虑到前面年份因父辈和子辈年龄导致向下偏误，因而更有理由确定真实的代际收入弹性，在前面年份较高的论断。因而，我们以表8的三年平均的父辈收入估计出的代际弹性为例，来讨论中国收入代际弹性系数的趋势。