特殊形式的倒向随机微分方程在金融市场中的应用

耿美华/金治明

【内容提要】首先，针对一类线性倒向随机微分方程，给出了g-鞅同鞅之间相互联系所满足的充分条件。通过该条件得到了经典的Black-Scholes模型下未定权益的公平价格过程以及最优增长投资策略的价格过程。其次，引入了非惩罚的非线性倒向随机微分方程，并通过惩罚比率的不同取值来讨论相关的经济学意义。

【关 键 词】倒向随机微分方程/g-鞅/完备市场/套利

        引言
        Pardoux & Peng[1]证明了一类非线性倒向随机微分方程(BSDE)存在解，基于这样的BSDE，Peng[2]提出了g-期望和g-鞅的概念。由于g的非线性，使得g-期望是一类非线性数学期望。Peng[2]，Chen and Peng[3]，Briand，Coquet，Hu，MUmin and Peng[4]等人研究了某些g-期望和g-鞅的概念，如：g-鞅的Dood-Mayer分解定理，g-鞅的上穿不等式等。许多学者进一步研究倒向随机微分方程在数理金融、随机控制、偏微分方程、随机微分对微和经济等领域的应用，如El Karoui，Peng and Quenez[5]，Chen and Kulperger[11]，Peng and Yang[9]等。
        本文通过建立特殊的g-鞅和经典鞅之间的联系，来进一步理解g-鞅的概念。将倒向随机微分方程的解（g-鞅）通过一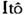 过程作为记帐单位来进行折现，在适当的条件满足下，可以找到一等价概率测度Q，使得折现后的过程是Q-鞅。为了将倒向随机微分方程应用到金融市场中，考虑经典的Black-Scholes模型，通过条件的限制，给出了未定权益的公平价格过程以及增长最优投资策略的价值过程，这是在没有任何经济含义下给出的解，也可以看作是倒向随机微分方程在金融市场中的应用。其次，我们讨论了带惩罚的非线性倒向随机微分方程，并通过惩罚比率的不同取值来讨论相关的经济学意义。可以看到倒向随机微分方程既可以表现完备市场也可以表现不完备市场，因此，作为一种新的研究金融市场的工具有其独特的优势。
        一、预备知识
         
         
         
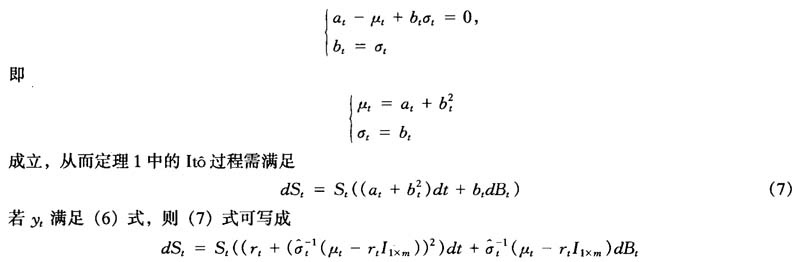
        该过程同Platen[8]所给出的增长最优投资策略一致。注意到这里并没有用到增长最优投资策略的定义，但是通过其一个性质得到了价值过程。即，当市场存在等价鞅测度时，以增长最优投资策略为记帐单位，则投资策略的折现价格过程是客观概率下的鞅过程。
        三、带惩罚的非线性倒向随机微分方程在金融市场中的应用
        考虑如下形式的倒向随机微分方程
         
         
    

【参考文献】
       [1]Pardoux, E. & Peng, S. Adapted solution of a backward stochastic differential equation[J]. Systems and Control Letters, 1990,14:55-61.
        [2]Peng Shige. BSDE and related g-expectation[J]. Pitman Research Noted in Math. Series, 1996,364:141-160.
        [3]Peng, S. Monotonic limit theorem of BSDE and nonlinear decomposition theorem of Doob-Mayer type[J]. Probab. Theory & Rel. Fields, 1999,113:473-499.
        [4]Briand, P., Coquet, F., Hu, Y., Mémin, J., Peng, S. A converse comparison theorem for BDDEs and related properties of g-expectation[J]. Electron. Comm. Probab., 2000,5:101-117.
        [5]ElKaroui, N., Peng, S. and Quenez, M. C. Backward stochastic differential equations in Finance[J]. Math, Finance, 1997,7:1-71.
        [6]Chen Zengjing and Peng Shige. A general downcrossing inequality for g-martingales[J]. Statistics & Probability Letters, 2000,46:169-175.
        [7]Peng Shige. Backward Stochastic Differential Equations, Nonlinear Expectation, Nonlinear Evaluations and Risk Measures[M]. Lecture Notes in Chinese Summer School in Mathematics, Weihai, 2004.
        [8]Platen, E. Arbitrage in Continuous Complete Markets[J]. Adv. in Appl. Probab., 2002,34(3):540-558.
        [9]Peng, S. and Yang, F. Duplicating and pricing contingent claims in incomplete markets[J]. Pacific Fconomic Review, 1999,4(3):237-260.
        [10]金治明.数学金融学基础[M].北京：科学出版社，2006.
        [11]Chen Zengjing and Reg Kulperger. Minimax pricing and choquet pricing[J]. Insurance Mathematics and Economics, 2006,38:518-528.^

转自《经济数学》(长沙)2009年1期第8～13页

【作者简介】耿美华，金治明，国防科技大学理学院（湖南长沙410073）