内容提要:本文在结构凯恩斯菲利普斯曲线框架内研究我国通胀动态行为,首先运用Gibbs抽样算法估计我国产出缺口,最后运用广义经验似然方法实施有限样本下的稳健结构经济计量分析。研究揭示我国通胀动态具有混合预期和非粘性的特征。基于此,本文提出降低宏观层面的通胀预期和提高货币政策执行力及透明度的政策建议。
关键词:通货膨胀动态,结构凯恩斯菲利普斯曲线,Gibbs抽样算法
一、前言
Gali和Gertler(1999)第一次用结构菲利普斯曲线来解释美国的通货膨胀动态机制,他们运用广义矩方法估计曲线之后,发现当期通货膨胀滞后项和未来期望项变量较好地解释了美国的当期通货膨胀机制。随后,Gali等(2005)进一步表明以当期通货膨胀滞后项和未来期望项为解释变量的结构菲利普斯曲线与欧盟数据高度拟合。Gali和Gertler的结构模型中用通胀滞后项代表后向搜索,以通胀期望项表示前向搜索,因此,我们可以基于历史数据估计结构菲利普斯曲线的参数,进而推断当期通货膨胀的滞后项和期望项的统计显著性来识别菲利普斯曲线是前向搜索型的新凯恩斯菲利普斯曲线,还是后向搜索型的旧凯恩斯菲利普斯曲线,或是前向和后向搜索同时存在的混合菲利普斯曲线。受Gali和Gertler(1999)研究的推动,我国学者石柱鲜等(2004)运用广义矩方法、陈彦斌(2008)运用最小二乘法估计了我国的结构凯恩斯菲利普斯曲线,研究结论表明我国数据支持混合菲利普斯曲线。
虽然Gali和Gertler(1999)的结构菲利普斯曲线能高度拟合历史数据,但他们在曲线中引入当期通胀期望项变量的处理方法却引起了争议。代表性的是Rudd和Whelan(2005)的方法论批评:广义矩方法在很大程度上支持的就是前向搜索,即使真实菲利普斯曲线是后向搜索。他们指出Gali和Gertler模型的通胀期望项系数估计在模型误设情况下高估,起因是模型设定时遗漏了更高阶的滞后项等相关回归量。他们建议菲利普斯曲线的识别应仅包含通胀滞后项,而不应纳入通胀期望项。Gali等(2005)回应说,尽管遗漏变量偏差在理论上无法消除,但Rudd和Whelan在单方程结构模型中附加更多的滞后项替代被遗漏变量的模型设定会导致同样的系数估计问题。
众所周知,广义矩方法的基本思想是要求矩函数的样本矩尽可能地与零接近来估计未知参数,理论依据是经济理论所蕴含的总体矩函数在参数真值处应具有零均值。在过度识别情形,矩函数的样本矩通常不可能准确地等于零。为确保估计量的有效性,实证研究者必须选择最优线性组合,常用的程度是使用某个初始一致估计量来估计这个最优线性组合。然而,越来越多的证据表明广义矩方法在有限样本下的表现并不如它的大样本性质那样良好,如Ahonji(1996)证明常用的二阶段估计量在有限样本下会出现参数低估,Hansen等(1996)建议使用连续更新程序来改善原有的二阶段广义矩估计。Stock等(2002)进一步从模型识别角度指出,广义矩估计的有限样本表现的典型问题是参数估计有偏和模型推断结论失真。
事实上,Rudd和Whelan(2005)的方法论批评的要点并不在于Gali和Gertler(1999)引入通胀期望项变量的建模方法是否恰当,而是在于研究者是否考虑到了有限样本下结构模型参数估计的偏误以及估计偏误导致的错误推断。从经济计量理论角度来考察,争议的实质是通胀期望项和滞后项在有限样本下是否能被广义矩方法正确识别。目前,国内结构菲利普斯曲线的研究主要运用的是广义矩方法,如曾利飞等(2006)的研究在方法论上面临Rudd和Whelan(2005)批评。基于此,本文首先基于我国1995年第1季度到2011年第2季度宏观季度数据建立我国结构菲利普斯曲线计量模型,为避免Rudd和Whelan(2005)批评,我们使用广义经验似然实施估计与推断。研究表明,结构凯恩斯菲利普斯曲线的广义经验似然估计量具有较好的有限样本表现,模型推断更稳健;我国结构凯恩斯菲利普斯曲线拒绝了“粘性通胀”假设,表明通胀路径可能具有内在的加速倾向。因此,控制通胀的关键一是降低宏观层面的“平均”通胀预期,二是提高货币政策执行力和透明度,减少政策滞后效应。
二、结构凯恩斯菲利普斯曲线
结构凯恩斯菲利普斯曲线是Gali和Gertler(1999)在新凯恩斯菲利普斯曲线基础上发展而来的。新凯恩斯菲利普斯曲线引入理性预期刻画经济动态行为,克服了旧菲利普斯曲线因其蕴含的适应性预期机制所招致的卢卡斯批判,在货币政策领域具有重要的理论价值和政策意义。但应用美国数据的大量实证研究表明,新凯恩斯菲利普斯曲线与观测数据不一致,早期文献将其归因于通货膨胀的内在动态行为。Gali和Gertler(1999)发现将通货膨胀滞后项引入新凯恩斯菲利普斯曲线后,历史数据较好地吻合了模型。
Gali和Gertler(1999)的模型即是结构凯恩斯菲利普斯曲线,它具有下面的形式
πt=a0+afEt(πt+1)+abEt(πt-1)+λχt+et (1)
其中πt代表通货膨胀率(Et,πt+1)表示在t期作出的t+1期预测。Gali和Gertler(1999)推导证明,如果方程(1)解存在,必须满足条件af+ab=1。令yt代表产出的对数,
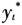
 定义了产出缺口χt,它通过Gibbs抽样算法估算。本文使用产出缺口作为推动项,也可使用其他经济变量作为推动项,如Gali等(2005)使用生产边际成本,Beyer和Farmer,2007)使用失业率。et表示误差项,它被假定为独立同分布随机变量,均值为0,方差为
定义了产出缺口χt,它通过Gibbs抽样算法估算。本文使用产出缺口作为推动项,也可使用其他经济变量作为推动项,如Gali等(2005)使用生产边际成本,Beyer和Farmer,2007)使用失业率。et表示误差项,它被假定为独立同分布随机变量,均值为0,方差为 。通常情况下,et与非前定变量χt和Et[πt+1]相关。t期的通货膨胀率的πt则用t-1期到t期价格水平的百分比变化率衡量。
。通常情况下,et与非前定变量χt和Et[πt+1]相关。t期的通货膨胀率的πt则用t-1期到t期价格水平的百分比变化率衡量。在方程(1)中用πt+1替代Et[πt+1]、πt-1替代Et[πt-1]得到下面的结构估计方程
πt=a0+afπt+1+abπt-1+γχt+vt (2)
其中vt=et+af (Eπt+1-πt+1)。陈彦斌,2008)基于微观调查数据采用普通最小二乘法估计方程(2),发现Eπt+1约为6.74,相比πt-1的系数-0.40不仅大很多而且符号相异。他解释为微观经济个体容易表现出高的通胀预期。Gali和Gertler(1999)利用美国数据采用广义矩方法估计方程,2)得出Eπt+1和πt-1的系数分别是0.78和0.23。然而,Altonji和Segal(1996)的模拟证据表明二阶段广义矩估计量在有限样本下是估计有偏的。Newey和Smith(2004)证明,相比广义矩估计量(GMM),广义经验似然估计量的高阶渐近偏差低于GMM;特别地,经验似然估计量的偏差对于工具变量的选取保持不变。Martins和Gabriel(2009)用广义经验似然方法和美国数据研究了方程(2)的估计和识别问题,表明广义经验似然估计相对广义矩估计更为稳健。
Gali和Gertler(1999)指出,若方程(2)的系数满足约束af+ab=1,表明通货膨胀粘性;反之则反之。通胀粘性的含义是当期通胀是上一期通胀和未来通胀的凸组合。如果期望通胀高于上一期通胀,现实通胀将处于两者之间,具体落点取决于af与ab的相对值。此时,通胀路径将与产出缺口的变化独立。如果通胀并非粘性,当期通胀将受到产出缺口变化影响,通胀将加速或者表现为通货紧缩。然而,Rudd和Whelan(2005)批评意味着通胀粘性结论可能源自所采用的广义矩估计方法,而真实的通胀动态路径可能是非粘性的。后文将采用广义经验似然方法对我国通胀动态实施结构经济计量分析来揭示这一点。
三、Gibbs抽样算法估计产出缺口
Gibbs sampler是蒙特卡洛马尔科夫方法的一个特例,最早由Geman和Geman在1984年提出,Gibbs sampler只需要计算在给定初值后变量的条件分布,因此大大降低了生成随机数时计算多元联合分布的复杂性,即在生成多元的随机样本时只要生成多个一元的条件分布的样本,而这些样本即可以看成是符合多元联合分布的随机样本。
Gibbs sampler的算法如下:设X=(X1,…,Xn,)的密度函数为π(X),在给定起始点
 的初值后,设第t次迭代开始时的估计值为χt-1,则第t次迭代过程如下:
的初值后,设第t次迭代开始时的估计值为χt-1,则第t次迭代过程如下: 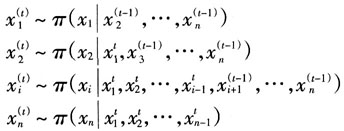
记
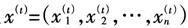 ,则
,则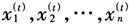 是具有马尔科夫链基本性质的随机样本。
是具有马尔科夫链基本性质的随机样本。基于Bayesian Gibbs sampler算法的状态空间模型算法如下:
建立状态空间模型
ξt=Fξt-1+vt (3)
yt=A′χt+H′ξt+wt (4)
vt~i.i.d.N(0,Q),wt~i.i.d.N(0,R),E(vtw′t)=0 (5)
其中F、A′、H′、Q、R为状态空间模型的超参数。定义
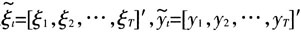 。
。在利用卡尔曼滤波和最大似然估计方法估计状态空间模型的方法中,模型的超参数被认为是已知的,在求解时先利用数值方法获得超参数的最大似然估计,然后通过卡尔曼滤波方法估计状态向量
 而在应用基于贝叶斯理论的方法时,模型的超参数和状态向量
而在应用基于贝叶斯理论的方法时,模型的超参数和状态向量 同时看作随机变量,在迭代过程中不断调整至相对收敛。
同时看作随机变量,在迭代过程中不断调整至相对收敛。Gibbs sampler算法在卡尔曼滤波算法中的应用可以概括为如下两步:
①带入初值,利用模型的超参数和观测数据得到
 。
。②利用
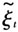 和观测数据得到模型的超参数,并将得到的超参数作为初值带回第一步,直到收敛。
和观测数据得到模型的超参数,并将得到的超参数作为初值带回第一步,直到收敛。其中,估计状态向量ξt的方法分为Q是正定矩阵和奇异矩阵两种情况。当Q为正定矩阵时,我们可以采用单步Gibbs sampler或者多步Gibbs sampler。单步Gibbs sampler是指在一次迭代中生成状态向量中的一个值,多步Gibbs sampler则是在一次迭代中生成整个状态向量。考虑到多步Gibbs sampler更有效率并且收敛更快,本文采用多步Gibbs sampler方法通过联合分布
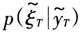 得到状态向量
得到状态向量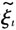 的估计。可以证明:
的估计。可以证明: 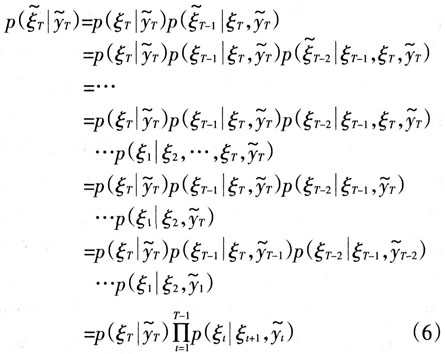
即
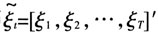 可以由ξT通过迭代生成。由于整个状态空间模型是线性和正态的,因此
可以由ξT通过迭代生成。由于整个状态空间模型是线性和正态的,因此 与
与 ,ξt+1(t=T-1,…,1)的分布也是正态的,即
,ξt+1(t=T-1,…,1)的分布也是正态的,即 
其中,ξt\t,ξt+1可以被看作是一个对ξt在给定ξt\t和ξt+1的相关信息的校正,ξt+1可以被看作是一个包含ξt\t所未含有的信息的外生变量:
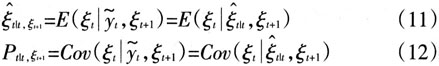
利用(12)式和(11)式可以得到
 ,根据(10)式并利用随机数的生成方法,即对协方差矩阵PπT进行乔列斯基(cholesky)分解,并将得到的下三角矩阵与任意服从标准正态分布的随机数相乘再加上期望
,根据(10)式并利用随机数的生成方法,即对协方差矩阵PπT进行乔列斯基(cholesky)分解,并将得到的下三角矩阵与任意服从标准正态分布的随机数相乘再加上期望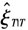 得到服从(10)式分布的随机数,从而得到ξT。
得到服从(10)式分布的随机数,从而得到ξT。根据(12)式可知,要得到ξt,必须要
 和Pt\t,ξt+1。得:
和Pt\t,ξt+1。得:
得:

因此新的预测误差为:

相应的MSE为:

从而可得:
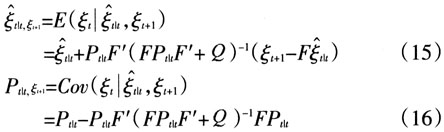
将(15)式和(16)式带入(9)式,利用随机数生成方法得到ξt。
当Q是奇异矩阵即|Q|=0时Pt\t,ξt+1将是奇异矩阵,因此无法得到ξt。假定矩阵Q的前J行是正定的,前J+1行是奇异的,则取前J行J列为矩阵Q*,因此Q*为秩最大的正定矩阵。同样,在生成ξt时,ξt+1只能取前J行,定义为
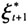 ,即
,即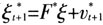 ,其中F*为F矩阵的前J行,
,其中F*为F矩阵的前J行,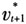 为vt+1的前J行。
为vt+1的前J行。将(6)式修改为:
 (17)
(17)将(10)式、(11)式和(12)式修改为:

将1995—2011年的GDP季度数据通过季度CPI换算为实际季度GDP并进行季节调整,从中选取1995—2011年的数据作为实际GDP季度数据,同时取1994年第1季度到第4季度的数据作为基期,得到1995—2011年的潜在GDP季度数据并进行季节调整作为潜在产出(图1),并根据定义得到相对产出缺口(图2)。
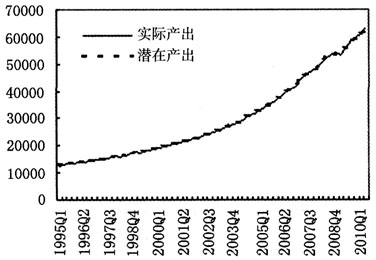
图1 1995—2011年实际产出与Gibbs潜在产出

图2 1995—2010年Gibbs相对产出缺口
四、广义经验似然估计
考虑结构凯恩斯菲利普斯曲线方程(1)
πt=a0+afπt+1+abπt-1+γχt+vt (20)
大部分国外文献使用利率作为工具变量,鉴于我国利率数据存在波动性缺乏问题,本文选用贷款余额dt和货币供给mt作为工具变量。假定推动项χt和通货膨胀πt的一阶滞后项与vt独立,令θ=(a0,af,ab,γ),z=(πt-1,πt,πt+1,χt-1,χt,dt,mt),模型(20)的矩条件是

获取观测数据后,样本矩条件的一般形式是

显然,在(22)式中如果令Pt=1/T,那么它是我们所熟知的广义矩估计量的矩条件方程组,进而可解出GMM估计量。如果我们选择Pt满足(22)式但并不约束Pt=1/T,那么我们解出的就是广义经验似然估计量(GEL)。它是下面的约束最优化问题的解

约束条件是
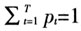 和
和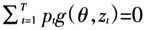 。(23)式中的函数hT(pt)度量pt与1/T的离散距离,它属于Cressie-Read函数族
。(23)式中的函数hT(pt)度量pt与1/T的离散距离,它属于Cressie-Read函数族hT(pt)=[Tδ,δ+1)]-1[(Tpt)δ+1-1] (24)
参数δ的不同选择对应不同的GEL类估计量,如δ=1是连续更新估计量(CU),δ=-1对应指数权估计量(ET),δ=0对应经验似然估计量(EL)。方程(23)需要采用数值方法求解,Newey和Smith(2004)将它表达为奇点解形式

其中λ是求解约束最优化问题(23)的拉氏乘子,ρ(λ′g(θ,zt))是标准化后的凸函数。在(25)式中给定θ,令u=λ′g(θ,zt),如果ρ(u)=2-1 (u2-1),是CU估计量;如果ρ(u)=-exp(u),则是ET估计量;如果ρ(u)=ln(1-u),对应EL估计量。经过复杂的推导可得pt=T-1ρ′(λ′g(θ,zt)),代入下面的方程组求解即得GEL估计量。

广义矩估计量要求预先一步估计以获取权重矩阵,这是导致其有限样本表现不佳的一个重要因素。为解释这一点,令θ0。表示参数真值,对给定的矩约束条件E[g(z,θ0)]=0,令A(θ)为依赖于θ的非奇异矩阵,定义
 ,那么有
,那么有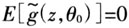 。在这个变换过程中,没有任何经济解释来选取A(θ)。因此,广义矩估计量会因为不同的A(θ)的选择导致有限样本下的不同表现。Stock(2002)详细解释了广义矩估计量在有限样本下易出现有偏估计和错误推断的原由,并指出实证研究中需要运用更稳健的其他备择方法来保证结构模型正确识别。Newey和Smith(2004)的重要文献表明广义经验似然估计量不仅避免了极易产生有偏估计结果的预先一步估计程序,它还具有独立于工具变量选取的优点。Newey和Smith证明广义经验似然估计量的高阶渐近偏差低于广义矩估计量,特别地,经验似然估计量的渐近偏差不随模型工具变量数增加而发生改变。下文将对模型(20)应用广义经验似然方法,并与广义矩方法的估计与推断结论进行比较。
。在这个变换过程中,没有任何经济解释来选取A(θ)。因此,广义矩估计量会因为不同的A(θ)的选择导致有限样本下的不同表现。Stock(2002)详细解释了广义矩估计量在有限样本下易出现有偏估计和错误推断的原由,并指出实证研究中需要运用更稳健的其他备择方法来保证结构模型正确识别。Newey和Smith(2004)的重要文献表明广义经验似然估计量不仅避免了极易产生有偏估计结果的预先一步估计程序,它还具有独立于工具变量选取的优点。Newey和Smith证明广义经验似然估计量的高阶渐近偏差低于广义矩估计量,特别地,经验似然估计量的渐近偏差不随模型工具变量数增加而发生改变。下文将对模型(20)应用广义经验似然方法,并与广义矩方法的估计与推断结论进行比较。(未完待续)
责任编辑:夏雨
