基于稳健主成分回归的统计数据可靠性评估方法

内容提要：稳健主成分回归（RPCR）是稳健主成分分析和稳健回归分析结合使用的一种方法，本文首次运用稳健的RPCR及异常值诊断方法，对2008年我国地区经济增长横截面数据可靠性做了评估。评估结果表明：稳健的RPCR方法能更好地克服异常值的影响，使估计结果更加可靠，并能有效地克服经典的主成分回归（CPCR）方法容易出现的多个异常点的掩盖现象；基本可以认为2008年地区经济增长与相关指标数据是匹配的，但部分地区的经济增长数据可能存在可靠性问题。
    关键词：统计数据可靠性 稳健主成分回归 异常值诊断
    作者简介：卢二坡（1976-），男，河南焦作人，南京大学应用经济学博士后，安徽财经大学应用统计研究所副教授，研究方向为统计理论方法与应用和经济统计分析研究；张焕明（1973-），男，湖北蕲春人，安徽财经大学应用统计研究所教授，研究方向为宏观经济数量分析。
    一、引言
    准确可靠的统计数据是把握经济运行情况、进行科学决策的基础。近年来，社会公众对中国官方公布的统计数据的关注度越来越高，其中不乏诸多质疑。一些学者从指标的相关性角度来检验政府统计数据的可靠性，如Klein和Ozmucur（2002）选取了中国1981-2000年15个有代表性的相关指标，使用经典的主成分回归方法，对中国经济增长数据的可靠性进行了评估[1]。阙里、钟笑寒（2005）进一步将Klein和Ozmucur（2002）的评估方法运用到了地区面板数据[2]。但这些研究存在如下不足：①这些研究没有考虑相关指标数据的可靠性。如果这些相关指标本身存在异常值或者可靠性问题，那么经典的主成分回归方法得到的估计结果将是不可靠的；②这些研究主要从总体上考察了经济增长与各相关指标的相关关系是否匹配，但没有对主成分回归拟合得到的异常值进行诊断。而经典的主成分回归方法并不能有效地诊断出数据集中的异常值；③经济增长率与各相关指标间的关系在经济发展的不同阶段可能是不稳定的，因此基于时间序列数据或面板数据的主成分回归对统计数据可靠性做出推断可能会出现偏差。
    文献中用经典的拟合方法（如主成分分析、最小二乘回归估计）得到的诊断工具去检测异常值。但经典的方法可能受到异常值的影响，以致模型拟合结果并不能检测出真正的异常值，这就是所谓的掩盖（masking）现象；并且经典的拟合方法还会使得一些正常的数据点表现为异常值，这就是所谓的淹没（swamping）现象。为避免这些现象，可以使用稳健统计方法。稳健统计的目的就是试图找到类似于当数据中没有异常值时的拟合结果，进而，从稳健拟合得到的大的残差中识别出异常值。本文将首次使用Hubert和Verboven（2003）提出的稳健主成分回归及相应的异常值诊断方法[3]，对我国地区经济增长横截面数据的可靠性进行评估。稳健主成分分析可以克服相关指标中的异常值对主成分的影响；稳健回归试图使求出的估计结果不受异常值的强烈影响，拟合的残差可以更好地识别出异常值。
    二、异常值诊断方法
    关于主成分回归的稳健估计和异常点诊断，国外已有学者进行了研究。Hubert和Verboven（2003）提出了一种新的稳健主成分回归方法RPCR[3]，并提供了相应的Matlab程序，该程序包含于稳健分析工具库LIBRA中①。RPCR方法的第一阶段是将稳健主成分分析方法ROBPCA应用于自变量x，并得到稳健主成分得分t；第二阶段是以稳健主成分得分t作为自变量，将因变量y对其进行回归，使用的回归方法是稳健的LTS（Least trimmed squred）估计。使用RPCR方法，还可以根据有关的诊断图有效地识别出正常观察测值、主成分的异常值和回归异常值。本文主要使用RPCR方法对我国地区经济增长统计数据进行诊断，该方法简要介绍如下。
    （一）稳健主成分分析
    RPCR的第一阶段是进行稳健主成分分析，使得到的主成分不受异常值的影响。RPCR使用的稳健主成分方法是Hubert et al.（2005）提出的ROBPCA方法[4]，该方法组合了两种稳健主成分分析方法的思想，一种是基于MCD估计的稳健的协方差矩阵方法，另一种是基于投影寻踪（Projection pursuit，下称PP）技术的方法。在ROBPCA中，PP部分被用于初始数据空间的降维，而基于MCD估计的一些思想则被用于这一低维数据空间。模拟结果表明，这一组合方法可以产生比投影寻踪方法更为精确的结果。
    
    ROBPCA方法的一个重要参数是允许数据集中未被污染的观测值的最高比例α，该方法默认α取值75%，即当数据集中至多包含25%的异常值时，该方法也能给出正确的分析结果。当怀疑数据集中所包含的异常值比例更高时，α最低可取50%。
    （二）稳健回归
    
    为估计式（2）的参数，一般使用重复加权的LTS估计方法[5]，该方法非常稳健，具有高达50%的破坏点（Breakdown point）。模型参数的LTS估计定义如下：
    
    （三）RPCR中主成分数目的选择
    RPCR的另一个重要问题是主成分数目的选择，最受欢迎的一种准则是交叉验证的最小化误差均方根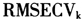，公式如下：
    
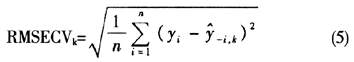
    式（5）中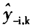，是将第i个观察值作为验证样本，先从数据集中删除第i个观察值，使用k个主成分得分进行主成分回归，再对其进行预测得到的预测值。具有最小的所对应的k就是最优的主成分的数目。然而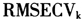，统计量并不适合于被污染的数据集，因为这个统计量也包含了对异常值的预测。为此，Hubert和Verboven（2003）建议使用稳健的RMSECV统计量（R-RMSECV）进行主成分数目的选择[3]。
    R-RMSECV是一种关于模型对新观测值预测能力的稳健度量。如果想察看模型对给定观测值的拟合情况，可以定义另一种类似的拟合程度准则——均方根误（RMSE）。RMSE准则是将式（5）中的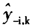替换为使用包括第i个观测值在内的所有观测值得到的拟合值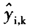。同样的，为避免异常值的影响，可计算不包括异常值在内的稳健的RMSE（RRMSE）。据此，Engelen和Hubert（2005）定义了另一种稳健的主成分选择统计量（RCS）如下[7]：
    
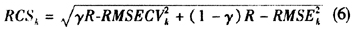
    式（6）中，γ∈[0，1]为调节参数。如果更看重拟合能力，则选择较小的γ（接近于0）；如果更看重预测的质量，则选择较大的γ（接近于1）。绘制对k的曲线图，可以轻易地选择最合适的k。
    （四）异常值的诊断方法
    1.主成分异常值的诊断
    在第一阶段的ROBPCA分析过程中，可以使用正交距离OD对得分距离SD诊断图识别出主成分得分空间（x空间）的异常值。该图的横轴绘制了每个p维观察值x的稳健得分距离SD，该图的纵轴是各个观察测值到其映射到k维主成分子空间的正交距离OD。
    为对主成分子空间的观测值进行分类，可画出SD和OD两条临界线。横轴的得分距离SD的临界值为，超过这一临界值的观测值可看作是主成分子空间的异常值。由于正交距离OD的精确分布未知，其临界值较难确定，Hubert等（2005）提供了该统计量的近似分布及临界值[4]。
    根据稳健主成分诊断图，可将x空间的观测值划分为四种类型：正常观测值（SD和OD均小）、好的主成分杠杆点（SD大，OD小）、正交异常值（SD小，OD大）以及坏的主成分杠杆点（SD大，OD大），后两种观测值是对经典的主成分分析结果有很大危害的异常值。
    2.回归异常值的诊断
    
    根据回归模型以及残差诊断图，可画出SD和RD的两条临界线，将观测值分为四类：正常观测值（SD小，RD绝对值小）、好的杠杆点（SD大，RD绝对值小）、纵向异常值（SD小，RD绝对值大）以及坏的杠杆点（SD大，RD绝对值大），纵向异常点和坏的杠杆点是对经典的OLS估计危害最大的异常值，因为它们扭曲了变量间的线性关系。
    三、指标选择和数据处理
    （一）指标选择
    
    在上述所选指标中，固定资产投资、消费品零售总额、出口额等3个指标是与支出法GDP各组成部分直接相关的；货运量是体现工业增长的良好指标；邮电业务量反映了作为服务业重要方面的信息化产业的发展状况；财政支出作为政府分配的重要组成部分，对经济增长有着不可低估的作用；税收收入是建立在增加值的活动基础上的，应该是个能较好地反映经济增长状况的指标；中国的经济增长严重依赖于信贷扩张，经济增长情况很有可能从这一指标中显现出来；就业和收入增长是经济增长的必然结果，其与经济增长应该有紧密的联系，因此，本研究还选取了农民人均纯收入、城镇居民可支配收入和城镇从业人员等指标；最后，能源消费特别是电力消费是经济发展的同步指标，应该能直接反映经济运行状况。这些指标与Klein和Ozmucur（2002）研究中相同的有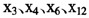等4个指标，与阙里和钟笑寒（2005）的研究中相同的有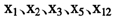等5个指标，与上述研究均不相同的有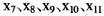等5个指标。

（未完待续）