内容提要:自2010年中国保监会允许国内试点变额年金市场之后,国内还没有相关文章对内部组合对冲模式下变额年金产品在精算领域面临的问题做出系统的阐述,本文在这方面给出了一套方法并结合实际进行了验证。通过经济情景发生器产生合理的经济情景,并基于假设的保单数据分析变额年金保证利益的合理定价区间;然后深入地讨论了动态对冲过程中各环节的设计并对结果进行分析,结果表明动态对冲可以显著降低各期损益以及累积损益的波动性;最后对变额年金的准备金和资本计算进行了国际比较,并给出了反映对冲与不反映对冲情况下的结果比较。
关键词:变额年金/经济情景产生器/动态对冲/后验分析作者简介:赵宇平,北京大学物理系学士,中国人民银行研究生部金融学硕士,现任阳光人寿保险公司精算部总经理助理(北京100020);龚昊翔,荷兰蒂尔堡大学金融学硕士,现任职于阳光人寿精算部(北京100020)。
2010年5月5日中国保监会发布了《关于开展变额年金保险试点的通知》以及《变额年金保险暂行管理办法》,目前市场上有两家保险公司已经分别推出了采用动态对冲方式和TIPP方式进行管理的两只变额年金产品。
目前就变额年金产品而言,国内精算领域尚无对于变额年金定价和风险管理有效性的系统性研究,本文研究采用内部组合对冲方式进行管理的变额年金产品的定价、对冲有效性测试和准备金计算,较为系统地阐述了从经济情景产生到动态对冲管理的整个过程。
一、经济情景产生器
经济情景分两种:风险中性世界情景和现实世界情景。
产生风险中性世界情景的目的是评估金融资产或负债的价值,因此产生的情景需要满足能复制市场上可观测到的金融工具的价格这一条件,称之为“市场一致性”(market consistency),可以将满足“市场一致性”的风险中性情景理解为一把“尺子”,这把“尺子”已经同市场上已知“长度”的物体(金融工具的价格)进行了校准,因而也可以用来测量未知“长度”的物体(保证利益或其他衍生品的价格)。
我们真正关心的风险是发生在真实的现实世界中的,风险在现实世界中的分布决定了需要提取的准备金或资本的数量。对冲会降低风险,因而也会降低需要提取的准备金或资本的数量。为了这个目的就需要产生现实世界中的经济情景,现实世界的经济情景可以用很多方法来产生,可以用历史数据、统计模型或者均衡模型来产生。
(一)风险中性世界情景
产生风险中性世界情景来评估变额年金中的保证的价值和计算对冲参数时,因为其同时受股票价格和收益率曲线的影响,我们需要产生股票价格和收益率曲线变动的联合分布情景。对于利率情景,有很多利率模型可供使用,这些利率模型主要分为两类:短期利率模型(如单因子或多因子的Hull White模型、BK模型、G2++模型等)和远期利率模型(HJM或LIBOR Market Model等)。执业者通常倾向于使用远期利率模型如LMM,原因一是在此类模型中,市场上交易的利率互换(Swap)价格本身(LIBOR利率)就是模型的输入参数,省去了校准收益率曲线的工作,另外更重要的是由于远期利率模型使用了更多的参数,因而能更好地校准互换期权的价格,但是研究者通常使用的是具备连续表达形式的短期利率模型,这不仅是由于其模型简洁便于分析,更重要的是相比远期利率模型而言,短期利率模型使用了较少的参数,因而具备更强的解释力。
在产生风险中性世界情景时,使用的是G2++利率模型和对数正态股票的联合模型,G2++利率模型和双因子Hull White模型是等价的(关于G2++利率模型的解释,请参考Brigo and Mercurio(2003)),但是具有更为对称的表达形式:


其中r(t)表示t时刻的瞬时短期利率,S(t)表示t时刻的投资账户价值,a和b分别表示驱动利率变动因素的回归速率,σ表示波动率,p表示不同随机运动间的相关系数,为了同初始收益率曲线校准一致,模型中的p(t)应该满足如下条件:

此模型中各个参数的校准需要知道利率互换期权和股票期权等衍生品的价格,由于中国目前尚没有这些工具,所以不可能从市场价格数据中得到当前市场隐含(market implied)的以上参数。但是可以通过对历史数据的拟合,得到以上相关系数的历史估计,并参照和中国相近且关联度较高的国外金融市场的当前状况进行调整而得到模型中的回归速率和各项波动率的估计。本文中采用的参数数值如表1所示。

图1是用G2++&LN模型产生的情景,左图是1000个股票指数的路径,右图是在某一个情景中,收益率曲线的演变过程。
通过历史数据拟合得到的股票历史波动率是即期波动率,它不同于上述模型中的远期波动率
 (t)。G2++&LN模型中股票的即期波动率是
(t)。G2++&LN模型中股票的即期波动率是 (t)、利率波动率以及股票和利率间相关系数的函数,具体关系如下式:
(t)、利率波动率以及股票和利率间相关系数的函数,具体关系如下式:
(二)现实世界情景
在用模型法产生现实世界情景时,利率部分可以使用Vasicek等模型,股票部分有LN、GARCH、RSLN2等模型可供选择。分别用以上几种股票模型对申万300股票指数从2000年1月1日至2011年9月30日的历史数据进行拟合,并对模型的拟合优度进行了比较,结果如表2。通过比较logL、SBC和AIC几个指标,可以看出RSLN2模型的拟合优度要好于GARCH和LN模型。

在拟合RSLN2时使用不同频率的数据得到的参数估计值会略有不同。出现这种现象的原因是:RSLN2模型中假定各期的股票收益率是不相关的,而实际上各期之间的股票收益率是具有关联性的。我们建议校准参数的时候使用的数据频率和实际的模拟频率(对冲频率)保持一致。
用日数据并使用RSLN2模型对申万300股票指数历史收益率的拟合结果如表3。


两个Regime的收益率区别不大,但是波动率区别极大。图2上方是从2000年以来申万300股票指数的日收益率,下方是根据RSLN2模型计算出的从2000年以来股票市场处于两个Regime中的概率,浅色曲线代表处于低波动率的Regime中的概率,深色曲线代表处于高波动率的Regime中的概率。
二、动态退保行为
一般投连产品的退保主要受退保费用、保单年度、缴费年期、年龄、性别等因素的影响,而影响变额年金产品退保模式的一个主要因素将是保证与账户价值的比率(In The Moneyness,ITM),账户价值低于保证时,客户的退保倾向将降低;账户价值高于保证时,客户的退保倾向将增加。如果在评估保证负债价值和计算对冲参数时不能把这个动态的退保行为反应进去将导致负债不真实,从而极大地影响实际对冲效果(增加对冲误差)。
一个合理的动态退保函数中要包括会影响动态退保的主要参数,如ITM,退保费用等。由于中国目前尚未有变额年金的退保数据,我们暂时假设客户的动态退保函数如下:
退保率(t)=基本退保率:Min(200%,Max(20%,1-a(ITM(t)-1)))
其中a为待校准的参数,a越高,ITM对退保的影响越大;ITM越高,退保率越低。
三、变额年金定价、对冲和利润测试
基于有效的经济情景发生器和动态退保行为的假设,可以对于变额年金产品进行定价和利润测试。定价是计算得出各种保证利益的市场一致性的价格,从而确定保证利益收取的标准;利润测试是基于计算的保证利益和其他费用测试在现实世界中利润分布,在测试过程中,将对冲的影响合理地考虑进去是关键。这两个步骤相互影响,执业者一般在进行多轮测试后为测定合理的保证利益收费和利润标准。假设在2011年10月12日发行了一只七年期的变额年金产品(投保人平均年龄50岁),产品提供最低身故保证和最低满期保证,最低满期保证为100%的保费,最低身故保证为GMDB(t)=Premium*
 。定价的利率曲线为当时的收益率曲线,参数采用第一部分中展示的数值。
。定价的利率曲线为当时的收益率曲线,参数采用第一部分中展示的数值。(一)保证利益的定价
使用蒙特卡洛模拟方法产生了风险中性世界的经济情景并对客户的动态退保行为进行假定之后,就可以求得变额年金中保证利益在发单时刻的价值,保证的价值为:

注:N:模拟次数
R(i,u):第i个情景u时刻的短期收益率
GMXB_payout(i,t):第i个情景中t时刻因保证
而导致的支出
GMXB_payout(i,t)=Death_no(t)Max(0,GMDB_Fund(i,t))+Mature_no(t)Max(0,GMMB-Fund(i,t))
Fund(i,t):第i个情景中t时刻的账户价值
由于变额年金产品不会在发单时刻将所有保证利益的成本收取,而是在账户存续期间以账户价值比例的方式进行扣除单位数,因此我们展示的保证利益价格是账户价值的一定比例,这也与目前市场通用的表达方式一致。表4展示了不同情况下(不同的资产波动率和利率水平)保证利益的成本。

可以看到:
1.最低满期利益保证的成本远高于最低身故利益保证;
2.随着股票波动率的上升,保证利益的成本上升,对于账户波动率的控制是公司能否盈利的一个关键因素;
3.随着利率的上升,保证利益的成本下降,因此公司在高利率环境发行变额年金产品比较有利。
(二)变额年金产品的利润测试
变额年金产品利润测试过程中最为核心的就是需要将对冲的效果考虑进去,为此,需要嵌套随机(Nested Stochastic)技术,首先产生现实世界的经济情景,然后在每个情景中的每个时点进行对冲操作和调整,为此需要根据当时的收益率曲线和股票价格重新进行模型校准后产生相应的风险中性情景,如此循环往复。这个计算过程是需要大量时间的,需要使用合适的软件平台并精心设计程序以及采取合理的误差降低技术来提高计算效率。
仅仅对冲股票价格风险往往是不够的,尤其在利率波动较大的经济环境下,所以一般至少需要对冲Delta和Rho两种风险,由于目前中国没有波动率产品,所以无法对冲Vega风险,管理Vega风险的一个办法是从投资策略上进行前端控制,即“波动率控制基金”(Target Volatility Fund),这种策略的基本原理就是根据市场上的隐含波动率来调整基金中权益类资产的占比,以使得基金总体的波动率控制在一个目标范围内。国内目前没有股票指数期权,可以考虑参考国内可转换债的价格中隐含的单个股票的隐含波动率以及同中国股市相关性较强的海外市场的隐含波动率来进行操作;另外也可以考虑根据最近的国内股票市场的实际波动率来进行调整。
在对冲Delta风险的时候还需要考虑基差风险,即对冲工具和被对冲的基金本身价格不完全同步所导致的风险。一个降低甚至消除基差风险的办法是“期货基金”(Future Fund),在这种方法下,基金中资产不再投资于传统的权益类资产,而是投资于股票期货,达到和直接投资股票一样的头寸,而剩余的资产则投资于无风险资产上,这样,由于对冲工具和被对冲的基金都为期货,基差风险就自然消失了。目前中国很多保险公司还不具备投资股票期货的条件,此时可以采取组合保险(Portfolio Insurance)的方式,即中国保监会《变额年金保险暂行管理办法》中所描述的方法。同时为了降低基差风险,可以投资于ETF或LOF基金。
对冲利率风险时最好的工具是利率互换,因为其本金本身并不交换,因而交易起来比较灵活,目前市场上流动性也比较好。但是有的保险公司还不具备投资利率互换的资格,这时可以选择债券作为对冲工具。债券的流动性更好,交易成本也不高,但是对交易规模有限制,所以现实的选择是保险公司可以计算利率风险,当其绝对额较小的时候可以暂不管理,等绝对风险数额大了的时候再通过债券来进行管理。
计算利率风险的时候,最好计算不同的关键利率久期(Key Rate Duration),选择一年、五年和十年作为关键利率,来分别代表收益率曲线运动的三种不同趋势:平移、翻转和陡峭。
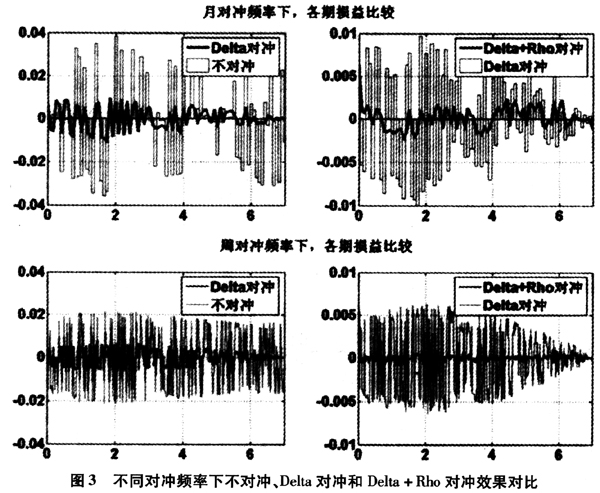
首先考察对冲对改善各期利润波动的影响。在接下来的演示中,仍然采取本段初设定的假设,并采用综合费用扣除2.25%。首先用Vasicek利率模型和RSLN2模型产生1000个真实世界的股票和利率情景,然后在每个情景中的每个时点(每月或每周)根据当时的股票价格和收益率曲线计算对冲参数Delta以及一年、五年和十年关键利率久期,然后据此调整对冲组合中的资产头寸,如此循环直至满期。在图3中展示了在某一个情景中,不对冲、Delta对冲和Delta+Rho对冲三种情况下各期损益的一个比较。上面两个图是在对冲频率为月的基础上得到的结果,下面两个图是在对冲频率为周的基础上得到的结果。
从图3中可以看到:
1.同不对冲相比,Delta对冲会显著降低利润的波动性;
2.在Delta对冲的基础上加进Rho对冲,会显著提高对冲的有效性;
3.随着对冲频率的提高,对冲的有效性将进一步提高。对冲频率的增加在提高对冲有效性的同时也会增加对冲的交易成本,因此,合理的对冲频率是在对冲有效性和对冲交易成本两者之间的一个权衡。
接下来考察累积损益的现值的分布情况,我们在周对冲频率的假设下进行了1000次模拟,模拟结果如图4所示。从图4中可以看出,不进行对冲的情况下,累积损益现值的分布类似对数正态分布,左侧尾部很长,出现严重亏损的概率较高;进行Delta对冲后,利润的波动降低,累积损益现值的分布变窄;进一步加进Rho对冲后,累积损益现值的分布迅速收窄,呈现出对称的分布,出现较大的亏损或收益的情况趋于消失(这三种情况下的CTE指标请参见本文的第五部分)。
对冲误差的产生实际上有几个原因:一是由于不能连续进行对冲交易而产生的离散误差,这部分误差会随交易频率的增加而降低;二是所谓的模型误差,是由于现实世界里股票价格和收益率曲线的演变过程不同于计算对冲时的假定模型而产生的。因此在进行利润的时候需要尽可能真实的产生真实世界模型才能刻画对冲的有效性。在计算对冲参数的时候使用单因子的Hull White模型和对数正态股票模型已经足够了,因为这个过程实质上是通过同市场价格进行校准而得到保证成本的过程,但是在产生真实世界情景的时候,认为至少需要使用双因子的Vasicek模型和RSLN2模型来产生股票和收益率曲线的联合过程,只有双因子的利率模型才能刻画收益率曲线更加丰富的变化模式,只有RSLN2模型才能比较真实地刻画股票价格在真实世界中的运动。这样,才能真实地考察对冲的有效性。
产生对冲误差的第三个原因是模拟误差,即由于我们的模拟次数不够导致的对冲参数计算和负债评估结果不准确带来的误差。这可以通过提高模拟次数并使用误差降低技术来改善。一般常用到的误差降低技术有:对偶抽样法(Antithetic Sampling)、矩匹配法(Moment Matching)、伪随机数法(Quasi-Random Sampling)和重要抽样法(Importance Sampling)。有研究表明,对长期的、有路径依赖性的保险产品,后两种方法实施起来有些问题,比较前两种方法,结果表明矩匹配法要优于对偶抽样法,模拟结果会更快地收敛于理论结果。
四、模型的后验分析
最后需要将模型放入真实世界中做一个检测,为了检验对冲的效率,挑选一个很极端的情况来看看对冲的表现,为此假设在2007年10月12日时发行先前提到的七年期产品。从下页图5可见,从发行后沪深300指数一路震荡下行至今,同时这段时间内收益率曲线的变动也比较剧烈,而这正为模型检验提供了丰富的数据环境。


假设周对冲在图6中比较了从产品发行至2011年10月12日期间,不对冲和Delta对冲两种情况下每周的损益情况,可以看出,同不对冲相比,Delta对冲显著降低了各期损益的波动。

在图7中比较了Delta对冲和Delta+Rho对冲两种情况下每周的损益情况。

可以看出,同Delta对冲相比,Delta+Rho对冲进一步降低了各期损益的波动。
对冲组合中股票的头寸和投资账户净值之间的关系如图8所示,其中浅灰色为投资账户净值,深灰色为对冲组合中股票的空头头寸,黑色实线为公司实际持有的股票头寸。从图中可以看出,对冲的本质实质上是“高买低卖”,这也正是期权成本产生的原因。

对冲组合中各年期债券的头寸如图9所示。

在发单时刻,GMXB负债对七年期利率最为敏感,由于设置的三个关键利率分别为一年、五年和十年,因此表现为其对五年和十年期利率最为敏感(注意图9中是各年期债券的头寸,而非敏感性,敏感性实际上为头寸再乘以年期),对短期(一年期)利率的敏感性很小;随着时间的推移,在发单四年后,此时产品的剩余期限已变为三年,这时GMXB负债对三年期利率最为敏感,表现为对一年期和五年期利率最为敏感,由于五至十年期利率水平对其已经没有影响,因此持有的十年期债券头寸降为零。
在周对冲频率下,从2007年10月12日至2011年10月12日,总体的对冲效果如表5所示。

可以看到,在周对冲频率下,在考虑了对冲交易成本后Delta对冲的有效性大致为75%,Delta+Rho对冲的有效性则接近90%。由于所进行的模拟没有反映客户的实际退保与我们所假设的动态退保的差异,所以实际中的对冲误差可能会比上述数字略低,这也反映了进行跟踪分析(monitor)的重要性,在变额年金正式运行后,我们需要跟踪对冲误差,对其进行归因分析,并据此不断修正模型假设并完善对冲策略。另外需要指出的是,在实务中通常不是进行固定频率的对冲操作,而是根据价格的变化幅度,或者对冲参数的变化幅度来进行对冲头寸的调整,这样会在提高对冲有效性的同时降低对冲交易成本。
五、变额年金的准备金以及资本
变额年金中GMXB负债的提取主要有两种方法,一是按照市场一致性的方法进行计算,如Solvency Ⅱ、IFRS4 Phase2以及目前的US GAAP,另外一种是按照现实世界情景中的CTE进行提取,如美国、加拿大和韩国等国家的法定准备金的提取;在这种方法下,各国的监管机构都会对现实世界经济情景产生器做出专门的校准规定。
如果使用现实世界情景中的CTE的方法提取准备金,一个相关的问题是是否可以将对冲反映进准备金的计算中,各国的规定不一样,美国的法定监管规定,只要对冲策略明确界定,法定准备金的计算是可以反映对冲的影响的,如果对冲的结果是由模型产生的,在计算法定准备金的时候最高可假设对冲有效性为70%,如果对冲的结果不是由模型产生的,在计算法定准备金的时候最高可假设的对冲有效性为30%。目前中国保监会对准备金的计算要是使用的是现实世界中的CTE(70%)的方法,但不允许反映对冲对准备金的影响。
使用现实世界情景CTE的方法计算准备金时,是否允许反映对冲对准备金数额的提取影响非常大。以先前的七年期产品为例,计算了在1000个真实世界情景下,不对冲、Delta对冲、Delta+Rho对冲三种情况下未来累积P&L的现值,其排序结果如图10所示。

在图11中比较在发单时刻不同的置信水平下CTE的数值,也就是在不同置信水平下应该提取的准备金或资本数量,可以看出,置信水平越高,需要提取的准备金或资本的数量也越高,同时,是否允许反映对冲的影响对实际提取的准备金或资本数量有非常大的影响。

如果使用CTE作为准备金的提取标准,在不同的置信度下,在不反映对冲、反映Delta对冲、同时反映Delta+Rho对冲的条件下,每单位保费在发单时刻分别需要提取的准备金数额如表6所示。

关于偿付能力资本的提取方法也主要有两种,一种是Solvency Ⅱ和经济资本所采取的方法,采用瞬时震荡法(Instantaneous Shock),假设资本市场发生瞬时震荡(震荡的幅度需要根据内部模型或标准公式进行校准),计算GMXB负债与资产各自的变化,从而计算出资本需求量;另外一种方法仍是现实世界中的CTE的方法,假设法定准备金为CTE(
 ),则偿付能力资本为一个更高的置信度
),则偿付能力资本为一个更高的置信度 下的CTE与准备金的差异:CTE(
下的CTE与准备金的差异:CTE( )-CTE(
)-CTE( )。
)。六、总结和展望
针对保监会推出的变额年金的相关管理办法的基础上较为系统地描述了内部组合对冲模式下产品在精算领域面临的问题。通过经济情景发生器产生合理的经济情景,并对G2++利率模型和对数正态股票的联合模型波动率提出了解析公式,这也为公司校验经济情景的合理性提出了一个办法。基于假设的保单数据,分析变额年金保证利益的合理定价区间。紧接着深入地讨论动态对冲对于变额年金风险管理的影响;对冲对于降低变额年金经营过程中产生的风险有极大的降低作用,在下行的资本市场环境中,对冲可以将损失减少70%~90%。在法定准备金计算方面,可以看出允许反映对冲效果将会对准备金提取产生重大影响。
变额年金产品作为一种创新性的保险产品,在国内的研究刚刚起步,本文初步探讨了内部组合对冲模式下变额年金定价和对冲方面的一些基本问题。在接下去的研究中,还有很多领域可以发掘。认为至少以下几方面也是业界比较关心的问题:
本文只讨论了内部组合对冲模式下变额年金的定价与管理,而没有涉及固定乘数平衡模式下变额年金产品的定价与管理,也没有涉及二者在管理上、定价上、客户吸引力等各个方面的对比。这是各个保险公司在选择产品策略的时候较为核心的问题。
在利润测试方面,我们只展示了保证部分的损益,没有测试在考虑变额年金产品实际收取的管理费用、实际支出的获得成本、运营维护成本后的利润指标(如内涵价值、利润边际和资本回报等)在不同情景下的实际分布,从而得出一些具体的、可用于选择合适费用率的指标体系。接下去的研究中,加入这些因素可以对变额年金整体业务的盈利状况做出更为科学的决策。
在模型方面,我们选取了一个模型作为市场一致性定价的开始,实际上,从业者会很关心应用不同模型对于定价和风险管理会产生的影响。参数的不同校准方法和不同模型将会衍生出不同的对冲策略,这些不同的对冲的结果对比与分析将对公司的风险管理模式产生影响。
参考文献:
[1]中国保险监督管理委员会.变额年金保险暂行管理办法,2010.
[2]中国保险监督管理委员会变额年金项目组.变额年金[M].北京:中国财经出版社,2010.
[3]Damiano Brigo and Fabio Mercurio, Interest Rate Models: Theory and Practice[M]. Berlin: Springer-Verlag, 2001.
[4]John C. Hull, Options, Futures and other Derivatives,
 editin[M]. New Jersey: Prentice Hall, 2002.
editin[M]. New Jersey: Prentice Hall, 2002.[5]Justin London, Modeling Derivatives in C++[M]. New York: John Wiley & Sons, Inc, 2004.
[6]Lenn Bloeh Mikkelsen. Pricing and Hedging Interest Bate Caps[D]. Denmark: Copenhagen Business School, 2010.
[7]Mary Hardy, Investment Guarantees: Modeling and Risk Management for Equity-linked Life Insurance[M]. New York: John Wiley & Sons, Inc, 2003.
[8]Stefan Singor, Efficient Simulation and Valuation of Embedded Options Using Monte Carlo Simulations[D]. The Netherlands: Delft University of Technology, 2009.^
