会员登录
会员注册内容提要：基于某一款万能险产品38个月的退保率样本数据，结合我国寿险业务的实际情况，利用广义线性模型对影响退保率的主要因素进行了分析。研究结果显示，源于消费者在购买保险的经济环境方面的差异，国外的退保率模型在我国并不适用。从我国实际情况出发，通过选择合适的解释变量，构建了新退保率模型，并分析了各解释变量对退保率的影响。
关键词：退保率/万能险/广义线性模型作者简介：高洪忠，中央财经大学中国精算研究院研究室主任，副教授，博士，主要研究方向：风险管理、保险精算等（北京100081）。
为了满足保监会全面风险管理的要求，保证寿险公司长期稳定健康发展，客观公正地对投资型寿险业务的流动性风险进行分析非常必要。导致寿险公司流动性风险上升的情形很多，包括信用恐慌、集中满期、额外承诺兑付、投资型业务萎缩、退保费用降为0后形成的退保大幅度上升等。对寿险公司而言，加强投资型业务退保风险的管理是流动性风险管理的重中之重。
为了防范退保风险，2008年10月保监会颁布了《关于加强退保业务管理的通知》（寿险部函[2008]103号），要求各寿险公司成立退保工作领导小组，并建立退保情况报送制度。随后，保监会同时出台了《关于建立寿险公司现金流预测临时报告制度的紧急通知（保监寿险[2008]1413号）》和《关于建立寿险业防范退保风险应急工作机制的通知》（保监寿险[2008]1433号），要求寿险公司从2009年起对分红险、万能险、投连险等单设账户管理的投资型寿险业务进行分类现金流预测。在寿险公司流动性风险管理和分类现金流测试中，合理估计各类投资型寿险业务的退保率是核心。
一、文献综述
在分析保单持有人的退保行为方面，国外学者提出了“财务危机”假说和“利率替代”假说。“财务危机”假说认为，寿险保单的现金选择权是一种应急基金，保单持有人可以通过行使该选择权获得资金。“利率替代”假说认为，短期内市场利率的变化会对寿险保单的价值产生影响，引起退保率的变化，且短期内两者变化方向相同；长期来看，利率的变化方向与退保率的变化方向可能相反。在对“财务危机”假设的论证中，国外学者认为失业率更能反映投保人所面临的财务状况。Outreville（1990）对美国和加拿大保险市场上的退保行为进行了实证研究，发现失业率对退保率有显著影响。Babbel（1995）通过研究发现，利率变化对寿险公司退保率有显著影响；Kuo（2003）利用美国1951年-1998年的保单失效率数据建立了一个VAR模型，发现短期内失业率对退保率有显著影响，而利率的短期影响不显著，长期来看，利率变化对保单退保率的影响比失业率更大一些。Richardson&Hartwell（1951）分析了高退保率的成因，认为影响退保率的因素包括：收入、职位、性别、年龄、投保经验、保费缴纳方式等，但是他们并没有采用数学模型进行分析。Buck（1960）认为，保单、投保人和代理人的性质对退保率有显著影响。Outreville（1990）检验了投保人将保单现金价值作为应急基金的假设。Bluhm（1993）认为提前清偿率的影响因素也可以作为退保率的影响因素。Richard和Roll（1989）构建了提前清偿率的模型，其自变量有融资动机、季节、保单年龄、月份和费用等。Browne，Carson&Hoyt（1999）认为，利率、个人收入、失业率、股市和房地产行情等因素是影响寿险保单退保率的重要因素。Dukes&Macdonald（1980）分析了道德风险与退保行为的关系。
国外学者在退保率模型方面的研究也很多。Kim（2005）用收益利差（等于市场利率与保单内嵌利率、退保费用的差额）、保单年龄、经济危机、失业率和季节等影响因素构造了logit模型和CLL模型。Cox&Lin（2006）针对退保率为0的记录占比较多的情形，提出了截0退保率模型，称为Tobit模型。Giovanni（2007）构造了随机利率市场模型，用于刻画投保人的退保行为。Milhaund，Loisel & Maume-Deschamps（2010）将logistic回归模型和分类回归模型应用到寿险组合中，证明了保险产品的一些特征可以解释投保人的退保行为。Loisel & Milhaud（2010）提出了一种退保率随机模型，它在缺乏数据的极端情况下更有效。
国内文献对于寿险保单退保问题的研究较少，且以定性描述为主。曹雪琴（2007）对退保行为的经济效应、制约因素和控制对策进行了定性分析。毛宏（2006）认为在保险定价时应考虑退保因素。朱曼芳（2007）强调应加强退保监控，及时发现退保行为的内在规律性。部分国内文献对退保行为进行了定量分析，楚军红（1997）利用“成本一收益法”分析了通货膨胀对于寿险需求的影响，认为通货膨胀率的上升引起投保人的退保行为。刘超（2006）构造结构方程模型分析了各个因素对客户退保行为的影响程度。展凯（2008）通过实证分析发现，失业率、利率、物价指数等变量对退保率的影响较大。杨舸、田澎（2008）提出了一个保单退保率分布模型，认为市场无风险利率、保险公司担保利率、资产波动率和保险公司盈余分配比例对退保率的影响较大。李国欣（2009）发现被保险人的预期收益率与其退保动机之间不存在单调关系。郭春燕，易丹辉（2007）利用Cox模型对传统寿险业务的退保进行了研究，给出了退保危险性比例。郭春燕（2010）年利用Cox模型建立了多个退保率预测模型。后两篇文献都是对传统寿险保单退保率的定量分析，认为被保险人死亡是保单失效的主要原因之一。
本文以某家寿险公司的某一款万能险产品为研究对象，以广义线性模型为研究工具，分析如何构建合适的退保率计量经济学模型。虽然是以万能险为例进行研究，但是该研究方法也适用于分红险、投连险等其他投资型寿险业务的退保率研究，具有很强的实际意义。
与已有的国内外相关文献相比，本文有以下创新点：（1）采用广义线性模型理论对退保率进行研究，可以由该随机模型得到退保率的置信区间，克服了确定性模型的缺点；（2）为了解决保单年龄对退保率影响的非单调型，在解释变量中引入保单年龄的一阶和负一阶项，提高了模型的解释能力；（3）剔除了失业率解释变量，引入居民收入增长率解释变量；（4）根据我国实际，考虑了保单持有人月回报率利差对退保率的影响，并将其作为新的解释变量引入模型中；（5）结合我国的投资型寿险业务进行分析，更能反映我国投资型业务的退保行为，具有更强的针对性；（6）从寿险公司预测退保率的目的出发，对多个模型进行了对比，建议采用完全由内部解释变量构成的模型4#，提升了退保率模型的实用性。
二、退保率模型的确定
目前寿险公司大多利用保单利差D为解释变量对退保率进行拟合和预测。这里D定义为市场利率与内嵌利率、退保费用之差。为了便于描述，这里首先对有关的符号进行说明。若将样本数据按承保月、日历月两个维度进行划分，可以把所有的观测值划分到各个单元中去。若用i表示承保月，j表示后续的各个日历月（i≤j），则可用（i，j）表示任一单元。用
表示单元（i，j）的退保率。目前寿险公司普遍采用以下几类S-型确定性退保率模型：
上面5个模型只涉及公司内部解释变量，在预测未来的退保率时具有很大的可操作性，这些模型目前被国外各寿险公司广泛采用。Kim（2005）利用寿险公司的内、外部解释变量，构造了两个退保率模型，即Logit模型、CLL模型：
（6）Logit模型：
对于这两个模型，首先根据经验数据对模型中的参数进行估计，然后对未来的退保率进行预测。这两个退保率模型用到了多个外部解释变量，包括：失业率、经济增长率、金融危机哑变量等，对寿险公司内部风险管理人员而言，这些变量都具有很大的不可预测性，使得这些模型的应用很受限制。
以上7个模型有一个共同点：采用保单利差D作为主要解释变量。根据保单利差D的定义和国内外的研究文献可知，通常情况下保单利差D与退保率之间存在着一条S型退保率曲线（如图1所示）。从图1可以看出，退保率与保单利差D之间应存在正相关关系，即保单利差D越大，退保率越高。
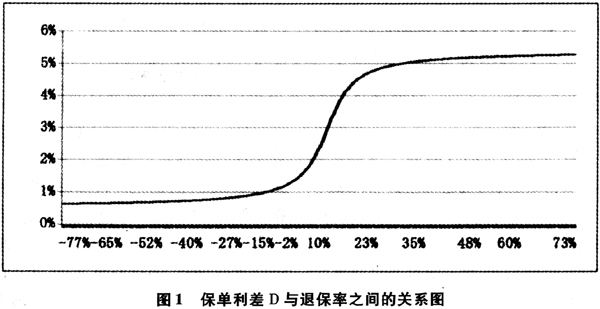
笔者通过分析后发现，若采用上面的7个模型对中国万能险业务的退保率进行分析，会得到荒谬的结论。例如，对本文后面所使用的样本数据，若采用上面的反正切模型，可得到下面的拟合结果：
从该拟合结果看，退保率与保单利差D之间呈现负相关关系，即D越大，退保率越小。采用上面其他几个模型对该样本数据进行分析，也得到了类似的结论。这说明，采用保单利差D分析中国万能险业务的退保率并不适合。
进一步分析后发现，上述7个模型是在西方发达国家处于经济发展相对平稳，通货膨胀水平较低的经济环境下提出的，但是它们对中国则不适用。笔者通过分析发现，我国万能险产品的保单持有人大多把购买保险作为一种中短期投资工具，希望能够在近几年内获得超过银行一年期存款利率的回报，准备持有到期的客户很少。因此应基于中国万能险保单持有人退保的实际情况，建立新的计量经济学模型，以分析中国万能险产品的退保率。
基于Kim（2005）的结果，并结合我国的实际情况，确定了新的内部解释变量，构建了一个新计量经济学模型。与已有的退保率模型相比，该模型更合理，与我国的保险实务更加吻合。这里采用的计量经济学模型为：
为了比较不同模型的似合效果，这里定义ARE统计量和RSE统计量，具体为：
三、经验数据的情况说明
2000年我国保险市场上出现第一款万能险产品，此后陆续出现了两全型、团体年金型等各种形态的万能险产品。从2005年起，市场上出现了专供银行渠道销售的简易型万能险产品，该类产品具有收费种类少、收费标准低、长期收益好、最低收益有保证等特点，使得万能险迅速成为各家寿险公司银保产品中的主导者。自2009年，保监会加强了对万能险产品的监管，要求各寿险公司每年报送万能险产品情况报告和万能险产品利润测试报告等风险分析报告。
以一款10年期趸交万能险产品为研究对象，以2011年8月1日作为评估日，以该款产品在2008年6月1日～2011年7月31日期间的数据为基础，在符合《万能保险精算规定》有关要求的前提下进行研究（如图2所示）。
基于图2的万能险结构图，下面给出该款万能险产品的一些必要特征：
1.最低结算利率。在合同有效期内个人账户价值的最低年结算利率为2.5%。
2.初始费用，即保险费进入万能账户之前扣除的费用。该产品的初始费用不高于5%。
3.退保费用，即保单退保时保险公司收取的费用，用以弥补尚未摊销的保单获取成本。该产品第一个保单年度的退保费用为个人账户价值的1%，后续年度无退保费用。
4.结算利率。该样本数据中包括该产品2008年、2009年、2010年的结算利率。
5.持续奖金。持续奖金是保险公司对持续有效的保单或持续交费的保单，满足合同约定条件时给予的奖金。
6.满期保险金。若被保险人于保险期满仍生存，按个人账户价值给付满期保险金。个人账户价值是指扣除初始费用后进入该账户的保费、保单持续奖金和计算的账户利息之和。
7.死亡风险保险费、保单管理费、手续费。该产品的这些费用占比较低，可忽略不计。
四、变量选择
考虑该款产品在2008年6月～2011年7月期间的退保情况。这里共有38个承保月，剔除保单数小于1的月份后剩余33个承保月，考虑各承保月在后续月份的退保情况。为了更合理地分析保单持有人的退保行为，这里以保单数为研究对象，而没有采用退保金额。这样，以各承保月和日历月为两个维度对样本数据进行划分，共得到621个单元，即621条记录。
1.保单年龄age及age1
Kim（2005）发现，在购买保单后的早期保单的退保率较高，在后期退保率又逐渐下降。为了反映退保率的这一特点，这里采用两个解释变量：age、1/age。由于部分单元的age=0，所以把后一个解释变量的分母由age调整为age+1，并记age1=1/（age+1）。对（i，j）单元，这两个解释变量分别为
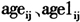。2.月回报率利差Delta0、Delta1、Delta2
记
ROY：1年期存款利率的月利率。
EMR：内嵌月收益率。该值越高，退保率越低。
SES：退保费用率。这里，若第一个保单年度退保则SES=1%，自第二个保单年度起SES=0%。
DIF=ROY-EMR-SES：表示退保与不退保之间的利差。对（i，j）单元，有：DIF（i，j）=ROY（i，j）-EMR（j）-SES（i，j）。
基于上面的记法，定义月回报率利差Delta0、Delta1、Delta2：
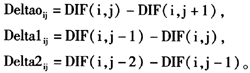
其中，Delta0反映了本月退保的回报率与下月退保回报率之间的差，而Delta1反映了滞后一个月的回报率利差，Delta2反映了滞后两个月的回报率利差。后两个解释变量用于反映目前普遍存在的退保行为的时滞效应。
3.消费者价格指数CPI
CPI是根据与居民生活有关的商品及劳务价格统计出来的物价变动指标，它通常是反映通货膨胀水平的重要指标。CPI对保单持有人的退保行为有一定影响，通常情况下，CPI与退保率成正相关关系。这里采用国家公布的月消费者价格指数作为CPI。对（i，j）单元，该解释变量只与j有关，记为
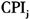。4.居民收入增长率IPP
统计分析发现，购买该款万能险产品的消费者绝大多数是城镇居民，这里用城镇居民月人均收入IPP作为解释变量。对（i，j）单元，该变量只与j有关，记为
。5.保单数N
用N表示各月承保的保单数。为了提高模型的适用性，这里考虑了各月份所承保的保单数N，作为广义线性模型拟合时的权重变量。对（i，j）单元，该变量只与承保月份i有关，记为
。6.退保率q
用q表示各月的退保率。样本数据中的每一条记录由被解释变量和若干解释变量组成，这里被解释变量是各月份的退保率q。对（i，j）单元，退保率是月份i承保的
张保单中在月份j退保的保单数与之比，记为。对寿险公司而言，（如表1所示）前5个解释变量属于内部变量，当一年期存款利率已知时它们可以由公司内部信息获得；6号、7号两个变量是外部变量，当预测退保率时需借助外部宏观经济模型进行合理估计。本文的研究目标是建立合适的计量经济学模型来预测退保率。为了提高估计的精确度和可操作性，应尽量考虑建立由内部变量构成的计量经济学模型。我国目前尚得不到可靠的月失业率数据，在此没有考虑该解释变量。
对本文所采用的样本数据，表2给出了各变量的数字特征（如表2所示）。
根据寿险公司所掌握的外部变量信息量的多少及其可信度，可以选用不同的广义线性模型。对前面的模型（1），满足
（1）采用表1中的1号～7号解释变量，记为模型1#。当采用此模型估计退保率时需要获得居民月人均收入增长率IPP和消费者价格指数CPI等相关信息。此时
（2）采用表1中的1号～6号变量作为解释变量，记为模型2#。当采用此模型估计退保率时需要获得居民月人均收入增长率CPI等相关信息。此时
（3）采用表1中的1号～5号和7号变量作为解释变量，记为模型3#。当采用此模型估计退保率时需要获得消费者价格指数IPP的相关信息。此时：
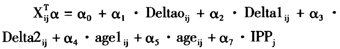
（4）采用表1中的1号～5号变量作为解释变量，记为模型4#。此时
五、结果分析
样本数据共包括621条记录，这里利用SAS软件的GENMOD过程，对这四个广义线性模型进行拟合，得到各模型的拟合结果（如表3所示）。
对于模型1#～模型4#，各解释变量的效应在1%的显著性水平上都是显著的。从表3看，各模型对样本数据拟合效果的优劣顺序为：
1#＞2#＞3#＞4#
其中，两元模型运算符“＞”表示在拟合优度意义上左边模型优于右边模型。记L为模型的似然函数值，为了选择合适的模型，可采用统计量-2*log（L）为工具进行模型的x2检验。通过计算发现，单纯从统计意义上说，在0.1%显著性水平上应采用模型2#；在0.5%及以下的显著性水平上应采用模型1#。通常情况下，模型2#是一个可接受的选择，但是在实际预测退保率时，考虑到外部解释变量IPP和CPI的不确定性，加之这四个模型的-2*log（L）差异较小，往往采用模型4#更可行。
模型4#中各参数的拟合结果（如表4所示）。从表4看，在0.01%显著性水平上各参数的效应都是显著的。
模型2#中各参数的拟合结果（如表5所示）。
从表5可以看出，各参数的效应也都显著性。
从表3可以看出，在上面所考虑的模型中，只有模型1#和模型3＃考虑了IPP对退保率的影响，且这两个模型中IPP的系数估计值差别不大。以模型3#为例，IPP的系数估计值为1.92，说明IPP越大，退保率越高；且IPP每增长1%，由（2）式可知，此时退保率增加
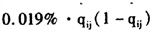。整体上看，IPP对退保率的影响较小，可以忽略。基于公司后续四年的业务发展规划，利用四个模型对未来各月份的退保率进行预测，（如图3所示）。根据已知的退保率数据，2011年8月、9月的退保率分别为0.7%、0.74%，通过与预测结果比较后发现，模型1#的预测结果最好，模型4#最差，与前面的拟合结果优劣顺序相一致。虽然模型1#～模型3#的拟合效果优于模型4#，但是考虑到它们需要获得CPI、IPP等外部信息，特别是在预测退保率模型时，对CPI、IPP的预测难度很大；同时考虑到这些解释变量对退保率的影响很小，几乎可以忽略，因此笔者建议，当可以获得CPI相关信息时，应该采用模型2＃对退保率进行估计；当CPI不可获得或可靠度低时，可采用模型4#。
六、结论与建议
投资型寿险产品的销售，为保险公司提供了大量的现金流入，特别是对那些成立时间较短的寿险公司，较高的保费收入对公司进一步发展具有极其重要的战略意义。但同时高退保率较导致较高的现金流出，影响着公司的长期稳定发展。基于以上的研究结果，结合目前我国经济环境和保险业所处的发展阶段，提出下列几条结论和建议。
1.合理确定业务的销售时间段
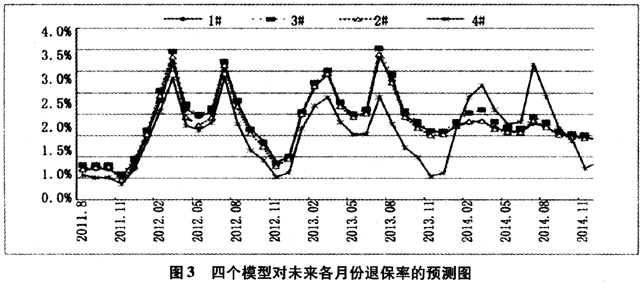
从图4可以看出，对于这里所考虑的保单，若其他因素不变，退保率随着保单年龄的增长而逐步上升，并在第22个月（等价于1.83年）退保率达到最高，然后逐渐降低。当保单年龄小于1年时退保率较短，是由于退保费用的作用。
目前，许多中小寿险公司往往采取高成本的展业方式为扩大业务规模，为公司实现盈利目标增加了难度。合理设定投资型业务的销售期限，有助于抵消高成本业务的影响，以平滑不同销售时间段的成本支出。
2.按销售时间段建立子投资账户
根据《万能保险精算规定》，保险公司可以在万能账户中对不同时段售出的万能保险业务建立不同的子万能账户，采用不同的结算利率。根据该产品的销售方式和初始费用的不同，可以考虑把该业务按不同时间段建立如下多个子投资账户，对各子投资账户采用不同的结算利率。通过该方式，可以在合理控制风险的前提下，降低投保人的退保率，同时提高公司风险管理的能力。
加强数据分析，合理确定结算利率。对业务的数据分析，有助于公司准确及时发现有关风险点，提高公司风险防范的能力。提取保单被保险人的有关信息和赔付数据，分析各风险因素对退保率的影响规律，合理控制风险。各寿险公司应研究各影响因素变化对退保率的影响，发现其规律性，合理确定各子万能账户的结算利率。
3.建立灵活的产品监管制度，降低消费者价格指数CPI对退保率的影响
在上面所考虑的四个模型中，只有模型1#和模型2#考虑了CPI对退保率的影响。从表3可以看出，这两个模型的CPI系数的估计值差别不大。以模型2#为例，CPI系数的估计值为0.11，意味着CPI越大退保率越高，且CPI每增长1个点，η增加0.11个点，由（2）式可知，此时退保率增加0.11·
（1-）。显然，CPI对退保率的影响较大，其根源是市场利率的影响。投保人购买投资型寿险产品的原因之一是在保证一定收益的基础上可以随时存取。目前许多投资型寿险产品的最低保证利率是基于产品开发时的市场利率确定的，往往不能满足投保人防御通货膨胀风险的投资需求。为了有效降低投资型产品的退保率，寿险公司应适当开发CPI敏感型产品，进而要求监管部门应放松对该类产品开发的监管。目前我国对投资型寿险产品实行产品开发批准制，在该监管模式下产品的预定利率是确定的，不能随市场利率的变化而调整。建议借鉴西方发达国家的保险监管方式，我国可考虑适当放宽寿险产品自主定价权，允许寿险公司开发一批利率敏感型产品。
4.建立利差风险准备金，防范回报率利差对退保率的影响
以模型4#为例，Delta0、Delta1、Delta2的系数估计值分别为-180.77、-91.32、-31.25，说明它们与退保率呈反方向变化，且对退保率的影响逐渐降低。这说明回报率利差有滞后效应。这里也尝试采用3个月时滞、4个月时滞等解释变量，发现效果都不显著。这说明回报率利差的滞后效应只有两个月，超过两个月后，效果不明显。
为了防范收益率不确定性对投资账户回报率利差所带来的影响、有效控制退保率，建议各寿险公司对部分投资型账户建立利差风险准备金制度。通过建立该制度，有助于寿险公司灵活应对市场利率的变化，根据当前的市场利率确定合理的结算利率，有效防范退保风险。
5.加强宣传力度，树立正确的舆论导向
目前我国投保人购买保险的心理仍不成熟，通过各种渠道加大宣传力度、提高客户的保险认知水平和认知能力非常重要。各寿险企业通过普及保险意识，不断提高客户对投资型寿险产品蕴含风险的认识，通过告知账户收益的不确定性等方式，切实落实保监会对《投保提示书》的要求，规范公司的展业行为。
负面新闻可能会引发群体性退保行为。媒体宣传具有放大效应，监管部门和保险公司应主动与宣传部门加强沟通，建立“退保信息发布机制”。通过对保险业的正面宣传，帮助公众正确理解投资型寿险产品的内在特征，引导投保人着眼于长期投资回报。
6.加强内控管理，提高公司的管理水平和投资收益率
为了有效控制退保率，各寿险公司应不断强化公司的内控体系，完善奖惩机制，加大对销售误导行为的惩罚力度。倡导诚信文化，树立良好的企业文化氛围，逐步培养销售人员的诚信意识和习惯。加强对新单售后的回访工作，保证在犹豫期内100%回访，提高回访成功率。
在资产安全的要求下提高投资收益率。各寿险公司应坚持把固定收益类产品作为主要投资渠道，保证收益的稳定性；适当扩大金融债券和权益类资产的投资比例，提高公司的投资绩效。加强市场风险分析，及时调整公司的投资结构，降低市场利率变化对公司带来的不利影响。
参考文献：
[1]曹雪琴.金融型退保与寿险产品完善的对策[J].上海保险，2007，(10)：52-55.
[2]楚军红.通货膨胀对寿险需求的影响机制分析[J].经济科学，1997，(3)：49-54.
[3]郭春燕，易丹辉.Cox模型和寿险退保研究中的比例危害性[J].统计与信息论坛，2007，22(3)：37-43.
[4]郭春燕.寿险保单早期退保率的预测[J].统计与咨询，2010，(1)：21-23.
[5]李国欣.基于被保险人有价格调整的预期收益率的退保行为研究[J].中国外资，2009，(9).
[6]刘超.结构方程模型在寿险公司客户退保行为中的应用[J].统计与决策，2006，(1)：40-41.
[7]毛宏.保险定价中各种风险因素的分析[J].商业研究，2006，(2)：55-56.
[8]杨舸，田澎.分红寿险退保率的最小二乘蒙特卡罗模拟研究[J].管理科学学报，2008，11(1)：95-100.
[9]展凯.中国寿险市场退保影响因素的实证分析[J].当代经济学，2008，30(4)：93-98.
[10]朱曼芳.关于寿险公司对退保进行监控的方法讨论[J].金融经济，2008，(4)：162-163.
[11]Babbel, D F. Asset-liability Matching in the Life Insurance Industry: The Financial Dynamics of the Insurance Industry. New York: Irwin Professional Publishing, 1995.
[12]Bluhm, W. F. Duration-Based Policy Reserves. Transactions of the Society of Actuaries, 1993,(45): 11-32.
[13]Browne, Mark J. Carson, J. M. Hoyt, R. E. Economic and Market Predictors of Insolvencies in the Life-Health Insurance Industry. Journal of Risk and Insurance, 1999, 66(4): 643-659.
[14]Buck, N. F. First Year Lapse and Default Rates. Transactions of the Society of Actuaries, 1960, 12(33): 258-293.
[15]Cox, S. It. Lin Y. Annuity Lapse Rate Modeling: Tobit or Not Tobit?, Society of Actuaries, 2006.
[16]Dukes, J. Macdonald, A. M. Pricing a Selected and Ultimate Annual Renewable Term Product, Transactions of the Society of Actuaries, 1980(32):547-584.
[17]Francois, O. J. Whole-Life Insurance Lapse Rates and the Emergency Fund Hypothesis, Insurance: Mathematics and Economics, 1990, 9(4): 237-306.
[18]Giovanni, D. D. Lapse Rate Modeling: A Rational Expectation, Finance Research Group Working Papers, 2007,(3): 5-29.
[19]Kim, C. Modeling Surrender and Lapse Rates with Economic Variables: North American Actuarial Journal, 2005, 56-70.
[20]Kim, C. Surrender Rate Impacts on Asset Liability Management. Asia Pacific Journal of Risk and Insurance, 2005,(1): 1-5.
[21]Kuo, W. Y. Tsai, C. H. Chen W. K., An Empirical Study on the Lapse Rate: The Co-integration Approach, Journal of Risk and Insurance, 2003,(70): 489-508.
[22]Loisel, S. Milhaud, X. From Deterministic to Stochastic Surrender Risk Models: Impact of Correlation Crises on Economic, European Journal of Operational Research, 2011. 214(2): 348-357.
[23]Milhaund, X. Loisel S Maume-Deschamps V. Surrender Triggers in Life Insurance: Classification and Risk prediction, Working Paper, 2010, 1-27.
[24]Outreville, J. F. Whole-life Insurance Lapse Rates and the Emergency Fund Hypothesis.Insurance: Mathematics and Economics, 1990,(4): 237-306.
[25]Richard, S. Roll R. Prepayments on Fixed-Rate Mortgage-Backed Securities, Journal of Portfolio Management, 1989,(15): 73-82.
[26]Richardson, C. B.Hartwell J. M., Lapse Rates, Transactions of the Society of Actuaries, 1951,(7): 338-374.
[27]Shen, W. Xu, H. The Valuation of Unit-linked Policies with or without Surrender Options. Insurance: Mathematics and Economics, Elsevier, 2005, 36(1): 79-92.^